Etant donnés deux entiers 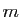 et
et 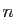 strictement positifs,
une matrice à
strictement positifs,
une matrice à 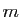 lignes et
lignes et
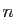 colonnes est un tableau rectangulaire de réels
colonnes est un tableau rectangulaire de réels
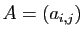 . L'indice de ligne
. L'indice de ligne 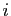 va de
va de 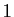 à
à 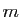 ,
l'indice de colonne
,
l'indice de colonne 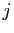 va de
va de 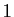 à
à 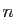 .
.
Les entiers 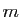 et
et 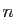 sont les dimensions de la matrice,
sont les dimensions de la matrice, 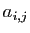 est son coefficient d'ordre
est son coefficient d'ordre 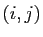 .
L'ensemble des matrices à
.
L'ensemble des matrices à 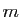 lignes et
lignes et 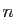 colonnes et à
coefficients réels est noté
colonnes et à
coefficients réels est noté
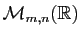 . Ce qui suit s'applique aussi, si on remplace
. Ce qui suit s'applique aussi, si on remplace
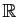 par
par
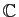 , à l'ensemble des matrices à coefficients complexes.
, à l'ensemble des matrices à coefficients complexes.
L'ensemble
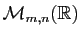 est naturellement muni d'une addition
interne (on peut ajouter deux matrices de mêmes dimensions terme à
terme) et d'une multiplication externe (on peut multiplier une matrice
par un réel terme à terme).
est naturellement muni d'une addition
interne (on peut ajouter deux matrices de mêmes dimensions terme à
terme) et d'une multiplication externe (on peut multiplier une matrice
par un réel terme à terme).
- Addition :
Si
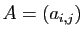 et
et
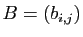 sont deux matrices de
sont deux matrices de
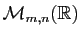 , leur somme
, leur somme 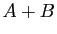 est la matrice
est la matrice
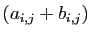 . Par
exemple :
. Par
exemple :
- Multiplication externe :
Si
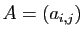 est une matrice de
est une matrice de
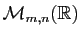 , et
, et 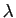 est un réel, le produit
est un réel, le produit 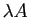 est
la matrice
est
la matrice
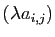 .
Par exemple :
.
Par exemple :
Observons que les opérations auraient le même effet si les
matrices étaient disposées comme des 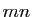 -uplets de réels
(toutes les lignes étant concaténées par exemple). Donc
-uplets de réels
(toutes les lignes étant concaténées par exemple). Donc
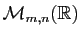 , muni de son addition et de sa multiplication
externe, est un espace
vectoriel, isomorphe à
, muni de son addition et de sa multiplication
externe, est un espace
vectoriel, isomorphe à
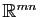 .
La base canonique de
.
La base canonique de
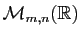 est formée des matrices dont tous
les coefficients sont nuls, sauf un qui vaut
est formée des matrices dont tous
les coefficients sont nuls, sauf un qui vaut 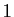 .
L'opération la plus importante est le produit matriciel.
.
L'opération la plus importante est le produit matriciel.
Nous insistons sur le fait que le produit 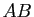 de deux matrices n'est
défini que si le nombre de colonnes de
de deux matrices n'est
défini que si le nombre de colonnes de  et le nombre de
lignes de
et le nombre de
lignes de 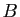 sont les mêmes.
Observons d'abord que la définition 1
est cohérente avec la
définition du produit d'une matrice par un vecteur, donnée au
chapitre précédent : si
sont les mêmes.
Observons d'abord que la définition 1
est cohérente avec la
définition du produit d'une matrice par un vecteur, donnée au
chapitre précédent : si 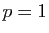 , la matrice
, la matrice 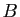 a
a 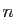 lignes et
lignes et 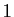 colonne, et le produit
colonne, et le produit 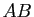 a
a 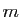 lignes et
lignes et 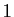 colonne. D'autre part,
appliquer la définition 1 revient à effectuer
successivement le produit de
colonne. D'autre part,
appliquer la définition 1 revient à effectuer
successivement le produit de  par chacune des colonnes de
par chacune des colonnes de 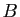 . Pour
effectuer ce produit, nous conseillons d'adopter la même disposition
que pour le produit par un vecteur, en plaçant
. Pour
effectuer ce produit, nous conseillons d'adopter la même disposition
que pour le produit par un vecteur, en plaçant 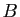 au-dessus et
à droite de
au-dessus et
à droite de  .
.
Posons par exemple :
La matrice  a 3 lignes et 2 colonnes, la matrice
a 3 lignes et 2 colonnes, la matrice 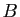 a 2 lignes et
4 colonnes. Le produit
a 2 lignes et
4 colonnes. Le produit 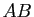 a donc un sens : c'est une matrice à 3
lignes et 4 colonnes.
a donc un sens : c'est une matrice à 3
lignes et 4 colonnes.
Le produit matriciel a toutes les propriétés que l'on attend d'un
produit, sauf qu'il n'est pas commutatif.
Ces propriétés se démontrent à partir de la définition
1.
La transposition est une notion importante, dont la justification
provient de la dualité, qui dépasse le cadre de ce cours.
Définition 2
Étant donnée une matrice
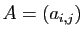 de
de
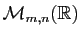 , sa
transposée est la matrice de
, sa
transposée est la matrice de
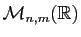 dont le
coefficient d'ordre
dont le
coefficient d'ordre 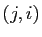 est
est 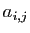 .
.
Pour écrire la transposée d'une matrice, il suffit de transformer
ses lignes en colonnes. Par exemple :
Observons que la transposée de la transposée est la matrice
initiale.
La transposée d'un produit est le produit des transposées, mais il
faut inverser l'ordre des facteurs.
Par exemple, en reprenant les matrices  et
et 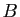 définies
ci-dessus :
définies
ci-dessus :
Observons que le produit d'une matrice par sa transposée est
toujours défini.
Le résultat est une matrice carrée (autant de lignes que de
colonnes) et symétrique.
Définition 3
Soit 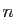 un entier strictement positif
et
un entier strictement positif
et  une matrice carrée à
une matrice carrée à 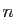 lignes et
lignes et 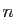 colonnes. On dit que
colonnes. On dit que  est symétrique si pour tous
est symétrique si pour tous
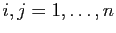 , ses coefficients d'ordre
, ses coefficients d'ordre 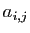 et
et 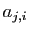 sont
égaux, ce qui est équivalent à dire que
sont
égaux, ce qui est équivalent à dire que  est égale à sa
transposée.
est égale à sa
transposée.
Le produit d'une matrice par sa transposée est toujours
une matrice symétrique. En effet :
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() et
et ![]() strictement positifs,
une matrice à
strictement positifs,
une matrice à ![]() lignes et
lignes et
![]() colonnes est un tableau rectangulaire de réels
colonnes est un tableau rectangulaire de réels
![]() . L'indice de ligne
. L'indice de ligne ![]() va de
va de ![]() à
à ![]() ,
l'indice de colonne
,
l'indice de colonne ![]() va de
va de ![]() à
à ![]() .
.
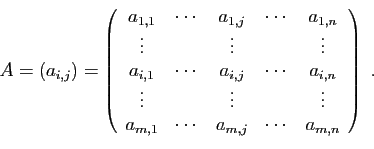
![]() est naturellement muni d'une addition
interne (on peut ajouter deux matrices de mêmes dimensions terme à
terme) et d'une multiplication externe (on peut multiplier une matrice
par un réel terme à terme).
est naturellement muni d'une addition
interne (on peut ajouter deux matrices de mêmes dimensions terme à
terme) et d'une multiplication externe (on peut multiplier une matrice
par un réel terme à terme).
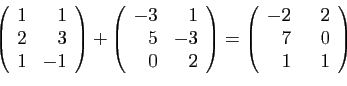
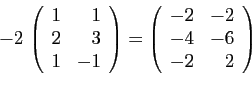
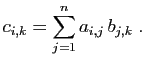
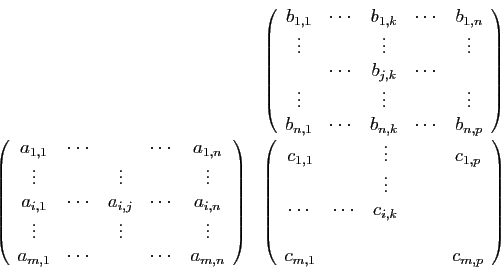
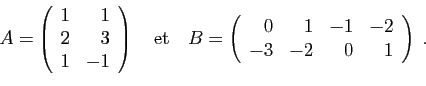
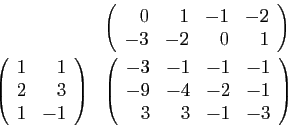
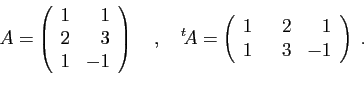
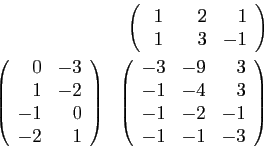
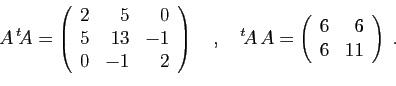
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales