-
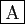
- Si la somme
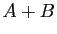 est définie, alors le produit
est définie, alors le produit 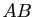 est défini.
est défini.
-
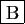
- Si la somme
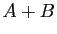 est définie, alors le produit
est définie, alors le produit 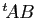 est défini.
est défini.
-
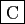
- Si le produit
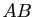 est défini, alors la somme
est défini, alors la somme 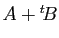 est définie.
est définie.
-
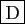
- Si les produits
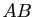 et
et 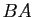 sont définis,
alors la somme
sont définis,
alors la somme 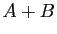 est définie.
est définie.
-
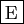
- Si les produits
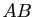 et
et 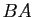 sont définis,
alors la somme
sont définis,
alors la somme 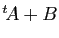 est définie.
est définie.
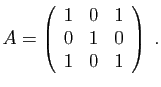
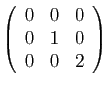
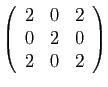
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales