 Si le produit
Si le produit 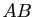 est défini, alors le produit
est défini, alors le produit 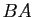 est défini.
est défini.
 Si la somme
Si la somme 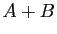 est définie, alors le produit
est définie, alors le produit 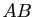 est défini.
est défini.
-
 Si le produit
Si le produit 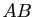 est défini, alors le produit
est défini, alors le produit
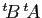 est défini.
est défini.
-
 Si la somme
Si la somme 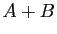 est définie, alors le produit
est définie, alors le produit
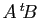 est
défini.
est
défini.
 Si les produits
Si les produits 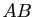 et
et 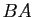 sont définis, alors la somme
sont définis, alors la somme 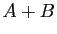 est
définie.
est
définie.
-
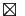 Si les produits
Si les produits 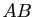 et
et 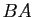 sont définis, alors la somme
sont définis, alors la somme 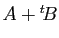 est
définie.
est
définie.
-
 Si les produits
Si les produits 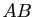 et
et  sont définis, alors la
somme
sont définis, alors la
somme 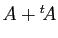 est
définie.
est
définie.
 Si les produits
Si les produits 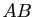 et
et  sont définis, alors la
somme
sont définis, alors la
somme 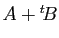 est
définie.
est
définie.
 Si le produit
Si le produit 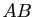 est défini, alors la somme
est défini, alors la somme
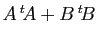 est
définie.
est
définie.
-
 Si le produit
Si le produit 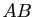 est défini, alors la somme
est défini, alors la somme
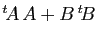 est
définie.
est
définie.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales