Le reste de ce chapitre est une révision du
programme de terminale sur les complexes.
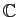 Les nombres complexes sont nés de la nécessité de donner un sens
à la racine carrée de nombres négatifs, pour résoudre les
équations algébriques. Dans l'ensemble des
réels, l'équation
Les nombres complexes sont nés de la nécessité de donner un sens
à la racine carrée de nombres négatifs, pour résoudre les
équations algébriques. Dans l'ensemble des
réels, l'équation 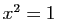 a deux solutions,
a deux solutions, 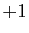 et
et 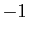 , mais
l'équation
, mais
l'équation 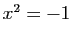 n'en a pas, puisque le carré de tout nombre
réel est positif ou nul. On décide d'appeler
n'en a pas, puisque le carré de tout nombre
réel est positif ou nul. On décide d'appeler
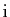 un nombre (imaginaire)
tel que
un nombre (imaginaire)
tel que
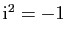 , puis d'appeler nombre complexe tout nombre de
la forme
, puis d'appeler nombre complexe tout nombre de
la forme
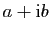 , où
, où 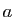 et
et 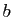 sont deux réels quelconques. Leur
ensemble est noté
sont deux réels quelconques. Leur
ensemble est noté
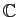 .
.
Ainsi tout nombre complexe 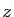 a une partie réelle, notée
Re
a une partie réelle, notée
Re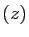 et une partie imaginaire, notée
Im
et une partie imaginaire, notée
Im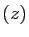 .
.
Re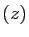 Im
Im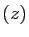 On représente ces nombres par les points d'un plan muni de deux axes
orthogonaux. L'axe horizontal porte les réels (qui sont les nombres
complexes dont la partie imaginaire est nulle). L'axe vertical porte
les nombres dits imaginaires purs, ceux dont la partie réelle est
nulle. Le point correspondant au
nombre
On représente ces nombres par les points d'un plan muni de deux axes
orthogonaux. L'axe horizontal porte les réels (qui sont les nombres
complexes dont la partie imaginaire est nulle). L'axe vertical porte
les nombres dits imaginaires purs, ceux dont la partie réelle est
nulle. Le point correspondant au
nombre
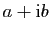 est placé à la verticale du réel
est placé à la verticale du réel 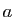 et
à l'horizontale de l'imaginaire pur
et
à l'horizontale de l'imaginaire pur
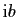 (figure
2). On dit que le nombre
(figure
2). On dit que le nombre
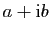 est
l'affixe du point qui le représente. Le point d'affixe 0
est l'origine, et on le note
est
l'affixe du point qui le représente. Le point d'affixe 0
est l'origine, et on le note 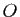 .
.
Figure 2:
Le plan complexe.
|
|
L'addition et la multiplication des réels s'étendent
aux nombres complexes sans difficulté particulière.
- addition :
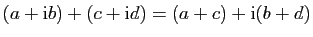 ,
,
- multiplication :
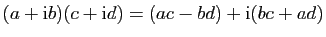 .
.
Soient 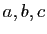 trois réels. L'équation du second degré
trois réels. L'équation du second degré
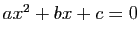 admet toujours des solutions, éventuellement complexes.
admet toujours des solutions, éventuellement complexes.
- si
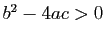 l'équation admet deux racines réelles,
l'équation admet deux racines réelles,
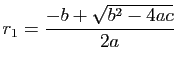
et
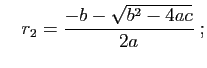
- si
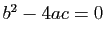 l'équation admet une racine réelle «double»,
l'équation admet une racine réelle «double»,
- si
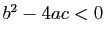 l'équation admet deux racines complexes,
l'équation admet deux racines complexes,
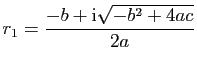
et
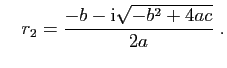
Ce résultat n'est pas étonnant, et vous le connaissez
déjà. Le miracle est que les complexes permettent de résoudre
non seulement les équations du second degré, mais toutes les
équations algébriques quel que soit leur degré.
Le théorème suivant porte en France le
nom de d'Alembert, bien qu'il ait été démontré par Gauss. Il
est partout connu comme le théorème fondamental de
l'algèbre.
Théorème 5
Soit 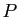 un polynôme de degré
un polynôme de degré
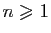 à coefficients complexes.
Le polynôme
à coefficients complexes.
Le polynôme 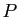 est un produit de
est un produit de  facteurs de degré
facteurs de degré 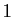 , à
coefficients dans
, à
coefficients dans
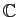 .
.
En d'autres termes, l'équation 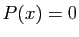 a toujours
a toujours  solutions ; certaines solutions peuvent être multiples, et elles sont
comptées avec leur ordre de multiplicité.
On traduit cette propriété en disant que
solutions ; certaines solutions peuvent être multiples, et elles sont
comptées avec leur ordre de multiplicité.
On traduit cette propriété en disant que
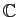 est
algébriquement clos.
est
algébriquement clos.
Voici quelques exemples.
Dans le plan complexe, le module est la longueur du segment joignant
l'origine au point représentant 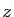 . L'argument est l'angle entre
l'axe des réels et ce segment, orienté dans le sens inverse des
aiguilles d'une montre (le sens trigonométrique). Le conjugué est
le symétrique par rapport à l'axe horizontal des réels (figure
3).
. L'argument est l'angle entre
l'axe des réels et ce segment, orienté dans le sens inverse des
aiguilles d'une montre (le sens trigonométrique). Le conjugué est
le symétrique par rapport à l'axe horizontal des réels (figure
3).
Figure 3:
Module, argument et conjugué d'un nombre complexe.
|
|
Observez qu'un nombre et son
conjugué ont le même module et que leur produit est le carré de
ce module.
Il est fréquent dans les calculs d'utiliser un conjugué pour
simplifier le résultat et le mettre sous la forme
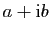 . Si
. Si
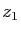 et
et 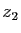 sont deux complexes, leur quotient s'écrit :
sont deux complexes, leur quotient s'écrit :
Voici un
exemple.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() Les nombres complexes sont nés de la nécessité de donner un sens
à la racine carrée de nombres négatifs, pour résoudre les
équations algébriques. Dans l'ensemble des
réels, l'équation
Les nombres complexes sont nés de la nécessité de donner un sens
à la racine carrée de nombres négatifs, pour résoudre les
équations algébriques. Dans l'ensemble des
réels, l'équation ![]() a deux solutions,
a deux solutions, ![]() et
et ![]() , mais
l'équation
, mais
l'équation ![]() n'en a pas, puisque le carré de tout nombre
réel est positif ou nul. On décide d'appeler
n'en a pas, puisque le carré de tout nombre
réel est positif ou nul. On décide d'appeler
![]() un nombre (imaginaire)
tel que
un nombre (imaginaire)
tel que
![]() , puis d'appeler nombre complexe tout nombre de
la forme
, puis d'appeler nombre complexe tout nombre de
la forme
![]() , où
, où ![]() et
et ![]() sont deux réels quelconques. Leur
ensemble est noté
sont deux réels quelconques. Leur
ensemble est noté
![]() .
.
![]() a une partie réelle, notée
Re
a une partie réelle, notée
Re![]() et une partie imaginaire, notée
Im
et une partie imaginaire, notée
Im![]() .
.
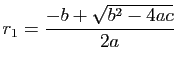 et
et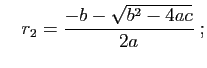
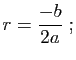
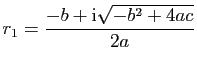 et
et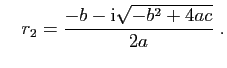

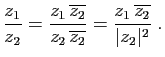
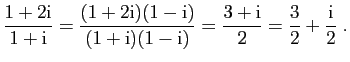
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales