Les formules données par
les trois théorèmes qui suivent vous seront souvent utiles.
Démonstration : Nous donnons d'abord la démonstration par récurrence. Nous verrons
ensuite une justification géométrique et une justification combinatoire.
L'hypothèse de récurrence est :
Pour 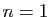 :
:
Supposons maintenant que 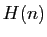 est vraie. Ecrivons :
est vraie. Ecrivons :
En appliquant 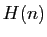 , on obtient :
, on obtient :
Le membre de droite s'écrit :
Nous avons donc démontré que :
c'est-à-dire que 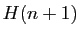 est vraie.
est vraie.
Voici maintenant une justification géométrique. Considérons un
rectangle dont la largeur et la hauteur valent respectivement 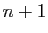 et
et
 unités (figure 1). Ce rectangle peut être
découpé en deux moitiés superposables. Chacune est formée de
unités (figure 1). Ce rectangle peut être
découpé en deux moitiés superposables. Chacune est formée de
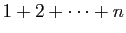 carrés de côté unité, et couvre une surface
égale à la surface du rectangle divisée par 2, soit
carrés de côté unité, et couvre une surface
égale à la surface du rectangle divisée par 2, soit 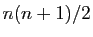 .
.
Figure 1:
La somme des  premiers entiers vaut
premiers entiers vaut 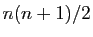 .
.
|
|
Voici maintenant une explication combinatoire. Autour d'une table
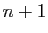 personnes sont assises et s'apprêtent à trinquer. Combien de
bruits de verre entendra-t-on ? Il y a deux manières de compter. La
première consiste à prendre les personnes dans l'ordre : la
première doit trinquer avec les
personnes sont assises et s'apprêtent à trinquer. Combien de
bruits de verre entendra-t-on ? Il y a deux manières de compter. La
première consiste à prendre les personnes dans l'ordre : la
première doit trinquer avec les  autres. La seconde, qui a
déjà trinqué avec la première, doit encore trinquer avec
autres. La seconde, qui a
déjà trinqué avec la première, doit encore trinquer avec 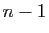 autres. Ainsi de suite jusqu'à la
autres. Ainsi de suite jusqu'à la  -ième personne, qui
ayant déjà trinqué avec les
-ième personne, qui
ayant déjà trinqué avec les 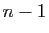 autres n'aura plus que la
autres n'aura plus que la
 -ième avec qui trinquer. On entendra donc
-ième avec qui trinquer. On entendra donc
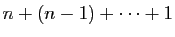 bruits de verre. La seconde manière de compter consiste à
remarquer que le nombre de bruits de verre est égal au nombre de
combinaisons de 2 personnes parmi
bruits de verre. La seconde manière de compter consiste à
remarquer que le nombre de bruits de verre est égal au nombre de
combinaisons de 2 personnes parmi 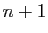 :
:
Les deux formules suivantes portent sur deux variables 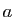 et
et 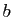 que
vous pouvez voir dans un premier temps comme deux réels.
Ces formules sont aussi
valables pour des nombres complexes, et plus généralement pour
des objets quelconques que l'on peut ajouter et multiplier de façon
commutative (par exemple des polynômes ou des fonctions de
que
vous pouvez voir dans un premier temps comme deux réels.
Ces formules sont aussi
valables pour des nombres complexes, et plus généralement pour
des objets quelconques que l'on peut ajouter et multiplier de façon
commutative (par exemple des polynômes ou des fonctions de
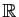 dans
dans
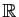 ).
La première généralise l'identité
remarquable
).
La première généralise l'identité
remarquable
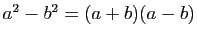 .
.
(Rappelons la convention 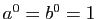 .)
Démonstration : La démonstration se fait par récurrence. L'affirmation
est vraie pour
.)
Démonstration : La démonstration se fait par récurrence. L'affirmation
est vraie pour 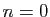 puisque :
puisque :
Supposons le résultat vrai pour  .
.
L'hypothèse de récurrence a été utilisée pour obtenir
l'avant-dernière égalité. Le résultat est vrai pour 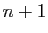 ,
donc pour tout
,
donc pour tout  .
.
Des cas particuliers du théorème 3 reviennent souvent
dans les calculs. Nous avons déjà rencontré le cas 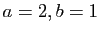 .
Vous pouvez retenir le suivant:
.
Vous pouvez retenir le suivant:
Plus généralement, on a la relation:
Démonstration : Il suffit de remarquer que :
 Une autre formule à connaître est celle du binôme
de Newton, qui généralise
Une autre formule à connaître est celle du binôme
de Newton, qui généralise
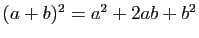 .
.
À cause de (6), les nombres
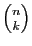 s'appellent les coefficients binomiaux.
Démonstration : Ici encore la démonstration se fait par récurrence, nous donnerons
ensuite une justification combinatoire. Pour
s'appellent les coefficients binomiaux.
Démonstration : Ici encore la démonstration se fait par récurrence, nous donnerons
ensuite une justification combinatoire. Pour 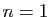 :
:
Supposons que la formule est vraie pour  et démontrons-la pour
et démontrons-la pour
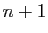 .
.
Pour la dernière égalité, nous avons appliqué la formule du
triangle de Pascal (3). Le résultat est démontré.
Voici maintenant la justification combinatoire. La quantité
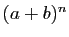 est le produit de
est le produit de  facteurs, chacun contenant deux termes
facteurs, chacun contenant deux termes
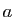 et
et 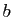 . Quand on développe le produit, on prend dans le premier
facteur un des deux termes, on le multiplie par un terme du second
facteur, ainsi de suite jusqu'au
. Quand on développe le produit, on prend dans le premier
facteur un des deux termes, on le multiplie par un terme du second
facteur, ainsi de suite jusqu'au  -ième facteur. Le produit obtenu
est égal à
-ième facteur. Le produit obtenu
est égal à
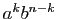 si on a choisi le terme
si on a choisi le terme 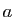 dans
dans  facteurs et le terme
facteurs et le terme 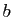 dans les
dans les 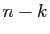 autres. Le nombre de produits
égaux à
autres. Le nombre de produits
égaux à
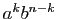 est le nombre de combinaisons de
est le nombre de combinaisons de  facteurs
parmi
facteurs
parmi  , soit
, soit
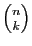 .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
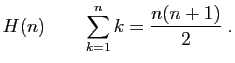
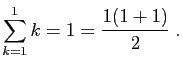
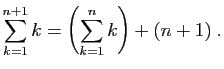
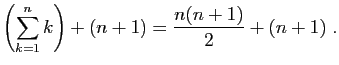
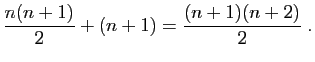
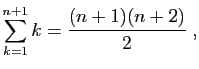
![]() et
et
![]() unités (figure 1). Ce rectangle peut être
découpé en deux moitiés superposables. Chacune est formée de
unités (figure 1). Ce rectangle peut être
découpé en deux moitiés superposables. Chacune est formée de
![]() carrés de côté unité, et couvre une surface
égale à la surface du rectangle divisée par 2, soit
carrés de côté unité, et couvre une surface
égale à la surface du rectangle divisée par 2, soit ![]() .
.
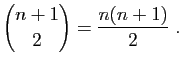
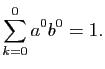
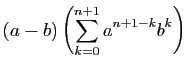
![]() .
Vous pouvez retenir le suivant:
.
Vous pouvez retenir le suivant:
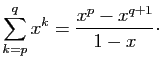
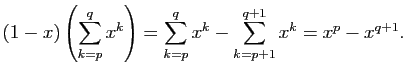
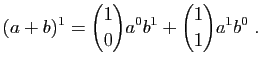
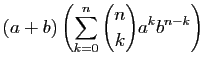
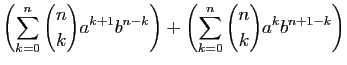
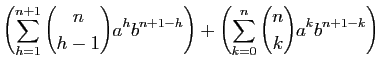
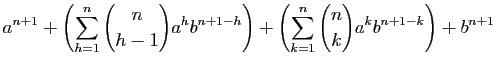
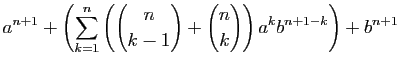
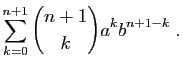
![]() est le produit de
est le produit de ![]() facteurs, chacun contenant deux termes
facteurs, chacun contenant deux termes
![]() et
et ![]() . Quand on développe le produit, on prend dans le premier
facteur un des deux termes, on le multiplie par un terme du second
facteur, ainsi de suite jusqu'au
. Quand on développe le produit, on prend dans le premier
facteur un des deux termes, on le multiplie par un terme du second
facteur, ainsi de suite jusqu'au ![]() -ième facteur. Le produit obtenu
est égal à
-ième facteur. Le produit obtenu
est égal à
![]() si on a choisi le terme
si on a choisi le terme ![]() dans
dans ![]() facteurs et le terme
facteurs et le terme ![]() dans les
dans les ![]() autres. Le nombre de produits
égaux à
autres. Le nombre de produits
égaux à
![]() est le nombre de combinaisons de
est le nombre de combinaisons de ![]() facteurs
parmi
facteurs
parmi ![]() , soit
, soit
![]() .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales