Nous commençons par les sommes.
L'écriture
se lit «
somme pour  allant de zéro à cinq de deux
puissance
allant de zéro à cinq de deux
puissance  ». C'est une
notation abrégée pour :
». C'est une
notation abrégée pour :
La lettre  est l'indice de sommation.
On la remplace
successivement par toutes les valeurs entières comprises entre les
deux bornes, qui sont 0 et
est l'indice de sommation.
On la remplace
successivement par toutes les valeurs entières comprises entre les
deux bornes, qui sont 0 et 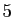 dans notre exemple. La
première borne, celle qui est écrite au-dessous du signe somme,
sera toujours inférieure ou égale à celle qui est au-dessus.
Les bornes peuvent elles-mêmes être des variables, mais elles sont
nécessairement différentes de l'indice de sommation. Par exemple,
pour tout entier naturel
dans notre exemple. La
première borne, celle qui est écrite au-dessous du signe somme,
sera toujours inférieure ou égale à celle qui est au-dessus.
Les bornes peuvent elles-mêmes être des variables, mais elles sont
nécessairement différentes de l'indice de sommation. Par exemple,
pour tout entier naturel  :
:
désigne la somme
Rappelons que, par convention, 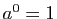 pour tout
nombre réel
pour tout
nombre réel 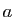 .
Prenez l'habitude d'écrire les sommes sous forme développée
quitte à introduire des points de suspension entre les premiers
termes et les derniers.
Voici quelques exemples d'égalités illustrant la
manipulation des indices et des bornes. Nous donnons sous chaque
exemple une écriture sous forme développée.
.
Prenez l'habitude d'écrire les sommes sous forme développée
quitte à introduire des points de suspension entre les premiers
termes et les derniers.
Voici quelques exemples d'égalités illustrant la
manipulation des indices et des bornes. Nous donnons sous chaque
exemple une écriture sous forme développée.
L'indice de sommation peut être remplacé par n'importe
quel autre : on dit que c'est une variable muette.
Observez que la borne peut être une des variables de la
quantité à sommer.
Dans cet exemple la quantité à sommer ne dépend pas de
l'indice de sommation : celle-ci a pour seul
effet de compter les termes. Attention, pour
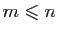 , il y a
, il y a
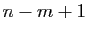 termes dans la somme de
termes dans la somme de 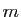 à
à  .
.
Une double somme est une somme de sommes, et on peut toujours
intervertir les deux.
Voici un enchaînement d'égalités, montrant que la
somme des puissances de 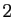 de
de 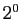 jusqu'à
jusqu'à 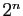 vaut
vaut
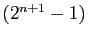 (c'est un cas particulier d'une formule à connaître que nous
verrons plus loin). Pour chaque ligne de calcul, nous donnons à
droite l'écriture sous forme développée. On rappelle que
(c'est un cas particulier d'une formule à connaître que nous
verrons plus loin). Pour chaque ligne de calcul, nous donnons à
droite l'écriture sous forme développée. On rappelle que 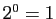 .
.
Ce que nous venons de voir pour les sommes s'applique aussi aux
produits. Le produit des entiers de 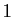 à
à
 intervient dans de nombreuses formules. C'est la
factorielle de
intervient dans de nombreuses formules. C'est la
factorielle de  . Elle se note «
. Elle se note «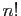 ».
».
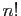
Il est souvent utile d'étendre la définition de la factorielle en
convenant que 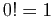 . Voici les premières valeurs.
. Voici les premières valeurs.
Si  est un entier positif,
un
est un entier positif,
un  -uplet désigne une liste ordonnée de
-uplet désigne une liste ordonnée de  objets.
On appelle permutation des nombres de
objets.
On appelle permutation des nombres de 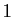 à
à  un
un  -uplet d'entiers
-uplet d'entiers
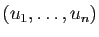 dans lequel chaque
entier entre
dans lequel chaque
entier entre 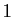 et
et  apparaît une et une seule fois.
Par exemple
apparaît une et une seule fois.
Par exemple
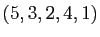 est une
permutation des nombres de
est une
permutation des nombres de 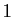 à
à 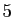 .
.
Théorème 1
Le nombre de permutations des nombres de 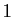 à
à  est
est 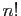 .
.
Démonstration : On montre le théorème par récurrence sur  .
.
Si 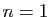 , la seule permutation des entiers de
, la seule permutation des entiers de 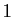 à
à 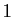 est
est 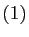 .
.
On suppose donc que le résultat est vrai pour l'entier  .
Montrons-le pour l'entier
.
Montrons-le pour l'entier 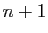 . Soit
. Soit  un entier tel que
un entier tel que
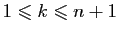 et comptons le nombre
et comptons le nombre 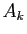 de permutations
de permutations
telles que 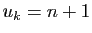 . À une telle permutation, associons
le
. À une telle permutation, associons
le  -uplet :
-uplet :
C'est une permutation des nombres de 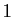 à
à  .
Inversement étant donnée une permutation
.
Inversement étant donnée une permutation
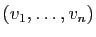 des entiers de
des entiers de 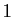 à
à  , alors
, alors
est une permutation des entiers de 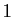 à
à 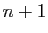 dont le
dont le  -ième terme est
-ième terme est 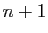 .
En appliquant l'hypothèse de récurrence, on obtient que
.
En appliquant l'hypothèse de récurrence, on obtient que
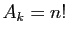 . Donc le nombre total de permutations des nombres de
. Donc le nombre total de permutations des nombres de 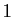 à
à 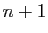 est :
est :
ce qui montre le résultat pour 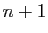 .
.
Pour ordonner  objets, il faut associer à chacun un
nombre entre
objets, il faut associer à chacun un
nombre entre 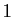 et
et  de sorte que chaque
nombre renvoie à un objet et un
seul. Il y a autant de manières de le faire que de permutations des
de sorte que chaque
nombre renvoie à un objet et un
seul. Il y a autant de manières de le faire que de permutations des
 premiers entiers :
premiers entiers : 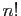 . Au tiercé, il y a
. Au tiercé, il y a 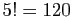 manières
d'ordonner les 5 premiers chevaux. Une seule donne l'ordre
d'arrivée, soit le quinté dans l'ordre,
et il y a
manières
d'ordonner les 5 premiers chevaux. Une seule donne l'ordre
d'arrivée, soit le quinté dans l'ordre,
et il y a 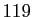 quintés dans le désordre.
Le nombre de combinaisons de
quintés dans le désordre.
Le nombre de combinaisons de  objets parmi
objets parmi  est le nombre
de manières de choisir
est le nombre
de manières de choisir  objets parmi
objets parmi  , sans distinguer leur ordre.
, sans distinguer leur ordre.
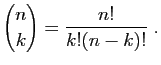 |
(1) |
La notation
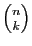
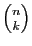
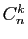 que nous utilisons ici, de préférence à l'ancienne
notation
que nous utilisons ici, de préférence à l'ancienne
notation 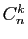 , est conforme aux programmes en vigueur et à
l'usage international. Nous conseillons de la lire «de
, est conforme aux programmes en vigueur et à
l'usage international. Nous conseillons de la lire «de  choisir
choisir  ».
».
La formule (1) correspond au raisonnement suivant. Pour choisir
 objets, on peut se donner une permutation des
objets, on peut se donner une permutation des  objets, et
décider d'en retenir les
objets, et
décider d'en retenir les  premiers. Parmi les permutations,
toutes celles qui auront en commun leurs
premiers. Parmi les permutations,
toutes celles qui auront en commun leurs  premiers nombres
conduiront au même choix. Il faut donc diviser par le nombre de
permutations des
premiers nombres
conduiront au même choix. Il faut donc diviser par le nombre de
permutations des  objets choisis, et par le nombre de permutations
des
objets choisis, et par le nombre de permutations
des 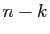 objets qui ne l'ont pas été.
objets qui ne l'ont pas été.
Observez que (1) ne change pas si on remplace
 par
par 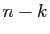 .
.
Choisir  objets parmi
objets parmi  (ceux que l'on garde) revient à en
choisir
(ceux que l'on garde) revient à en
choisir 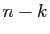 (ceux que l'on laisse).
(ceux que l'on laisse).
Voici une autre expression de
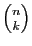 .
.
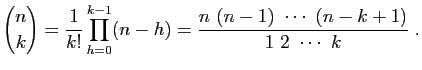 |
(2) |
Notez qu'il y a  facteurs au numérateur, comme au dénominateur.
On obtient cette formule en simplifiant le quotient
facteurs au numérateur, comme au dénominateur.
On obtient cette formule en simplifiant le quotient 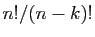 dans
(1).
dans
(1).
On peut aussi raisonner comme suit. Il y a  façons de choisir le premier objet, puis
façons de choisir le premier objet, puis 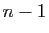 de choisir le
second (puisqu'un objet a déjà été choisi), etc. Pour
choisir le
de choisir le
second (puisqu'un objet a déjà été choisi), etc. Pour
choisir le  -ième objet, il reste
-ième objet, il reste
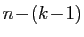 possibilités. Ceci
correspond au numérateur de (2). Cette manière de
procéder retourne une liste ordonnée. Il faut donc diviser par le
nombre d'ordres possibles des
possibilités. Ceci
correspond au numérateur de (2). Cette manière de
procéder retourne une liste ordonnée. Il faut donc diviser par le
nombre d'ordres possibles des  objets choisis, qui est
objets choisis, qui est 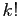 .
.
Observez les relations suivantes, faciles à déduire de
(1) ou (2) et de la définition de la factorielle.
Pour calculer
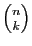 en pratique, on n'utilise ni (1)
ni (2). Le calcul récursif par la formule du
triangle de Pascal (connue des indiens, des chinois et des
arabes bien avant Pascal)
est beaucoup plus rapide.
en pratique, on n'utilise ni (1)
ni (2). Le calcul récursif par la formule du
triangle de Pascal (connue des indiens, des chinois et des
arabes bien avant Pascal)
est beaucoup plus rapide.
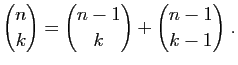 |
(3) |
Nous conseillons au lecteur de démontrer cette formule à partir des
expressions (1) et (2). Voici la justification
combinatoire. Supposons que parmi les  objets dont
objets dont  doivent
être choisis, l'un d'entre eux soit distingué (disons qu'il est
rouge). Parmi les choix possibles de
doivent
être choisis, l'un d'entre eux soit distingué (disons qu'il est
rouge). Parmi les choix possibles de  objets, certains ne contiennent
pas l'objet rouge, d'autres le contiennent. Les premiers
sont au nombre de
objets, certains ne contiennent
pas l'objet rouge, d'autres le contiennent. Les premiers
sont au nombre de
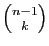 , car les
, car les  objets sont choisis
parmi les
objets sont choisis
parmi les 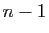 différents de l'objet rouge. Les choix contenant
l'objet rouge sont au nombre de
différents de l'objet rouge. Les choix contenant
l'objet rouge sont au nombre de
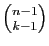 car l'objet rouge
ayant été retenu, il reste
car l'objet rouge
ayant été retenu, il reste 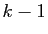 objets à choisir parmi les
objets à choisir parmi les
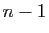 autres.
Voici, disposées en triangle, les valeurs de
autres.
Voici, disposées en triangle, les valeurs de
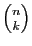 pour
pour  allant de 0 à
allant de 0 à 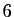 .
.
Chaque valeur est la somme de celle qui est
au-dessus, et de celle qui est à gauche de celle qui est
au-dessus. S'il n'est pas indispensable de connaître ce tableau
par c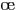 ur, il est souvent utile de savoir le réécrire rapidement.
ur, il est souvent utile de savoir le réécrire rapidement.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
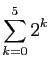
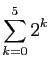
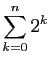
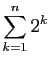
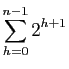
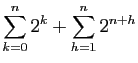
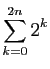
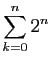
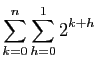
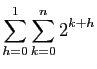
![]() de
de ![]() jusqu'à
jusqu'à ![]() vaut
vaut
![]() (c'est un cas particulier d'une formule à connaître que nous
verrons plus loin). Pour chaque ligne de calcul, nous donnons à
droite l'écriture sous forme développée. On rappelle que
(c'est un cas particulier d'une formule à connaître que nous
verrons plus loin). Pour chaque ligne de calcul, nous donnons à
droite l'écriture sous forme développée. On rappelle que ![]() .
.
![\begin{displaymath}
\begin{array}{lcl\vert cl}
\displaystyle{\sum_{k=0}^n 2^k}&=...
...cdots+2^n) [2ex]
&=&
2^{n+1}-2^0
&=&
2^{n+1}-1\;.
\end{array}\end{displaymath}](img38.gif)
![]() à
à
![]() intervient dans de nombreuses formules. C'est la
factorielle de
intervient dans de nombreuses formules. C'est la
factorielle de ![]() . Elle se note «
. Elle se note «![]() ».
».
![]()
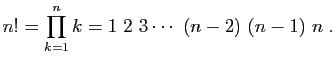
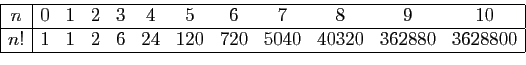
![]() est un entier positif,
un
est un entier positif,
un ![]() -uplet désigne une liste ordonnée de
-uplet désigne une liste ordonnée de ![]() objets.
On appelle permutation des nombres de
objets.
On appelle permutation des nombres de ![]() à
à ![]() un
un ![]() -uplet d'entiers
-uplet d'entiers
![]() dans lequel chaque
entier entre
dans lequel chaque
entier entre ![]() et
et ![]() apparaît une et une seule fois.
Par exemple
apparaît une et une seule fois.
Par exemple
![]() est une
permutation des nombres de
est une
permutation des nombres de ![]() à
à ![]() .
.
![]() , la seule permutation des entiers de
, la seule permutation des entiers de ![]() à
à ![]() est
est ![]() .
.
![]() .
Montrons-le pour l'entier
.
Montrons-le pour l'entier ![]() . Soit
. Soit ![]() un entier tel que
un entier tel que
![]() et comptons le nombre
et comptons le nombre ![]() de permutations
de permutations
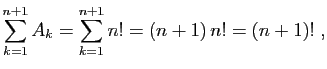
![]() objets, il faut associer à chacun un
nombre entre
objets, il faut associer à chacun un
nombre entre ![]() et
et ![]() de sorte que chaque
nombre renvoie à un objet et un
seul. Il y a autant de manières de le faire que de permutations des
de sorte que chaque
nombre renvoie à un objet et un
seul. Il y a autant de manières de le faire que de permutations des
![]() premiers entiers :
premiers entiers : ![]() . Au tiercé, il y a
. Au tiercé, il y a ![]() manières
d'ordonner les 5 premiers chevaux. Une seule donne l'ordre
d'arrivée, soit le quinté dans l'ordre,
et il y a
manières
d'ordonner les 5 premiers chevaux. Une seule donne l'ordre
d'arrivée, soit le quinté dans l'ordre,
et il y a ![]() quintés dans le désordre.
Le nombre de combinaisons de
quintés dans le désordre.
Le nombre de combinaisons de ![]() objets parmi
objets parmi ![]() est le nombre
de manières de choisir
est le nombre
de manières de choisir ![]() objets parmi
objets parmi ![]() , sans distinguer leur ordre.
, sans distinguer leur ordre.
![]() objets, on peut se donner une permutation des
objets, on peut se donner une permutation des ![]() objets, et
décider d'en retenir les
objets, et
décider d'en retenir les ![]() premiers. Parmi les permutations,
toutes celles qui auront en commun leurs
premiers. Parmi les permutations,
toutes celles qui auront en commun leurs ![]() premiers nombres
conduiront au même choix. Il faut donc diviser par le nombre de
permutations des
premiers nombres
conduiront au même choix. Il faut donc diviser par le nombre de
permutations des ![]() objets choisis, et par le nombre de permutations
des
objets choisis, et par le nombre de permutations
des ![]() objets qui ne l'ont pas été.
objets qui ne l'ont pas été.
![]() par
par ![]() .
.
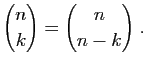
![]() .
.
![]() façons de choisir le premier objet, puis
façons de choisir le premier objet, puis ![]() de choisir le
second (puisqu'un objet a déjà été choisi), etc. Pour
choisir le
de choisir le
second (puisqu'un objet a déjà été choisi), etc. Pour
choisir le ![]() -ième objet, il reste
-ième objet, il reste
![]() possibilités. Ceci
correspond au numérateur de (2). Cette manière de
procéder retourne une liste ordonnée. Il faut donc diviser par le
nombre d'ordres possibles des
possibilités. Ceci
correspond au numérateur de (2). Cette manière de
procéder retourne une liste ordonnée. Il faut donc diviser par le
nombre d'ordres possibles des ![]() objets choisis, qui est
objets choisis, qui est ![]() .
.
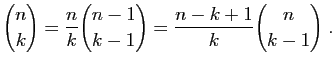

 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales