Essayez de bien rédiger vos réponses, sans vous
reporter ni au cours, ni au corrigé.
Si vous souhaitez vous évaluer, donnez-vous deux heures ; puis comparez
vos réponses avec le corrigé et comptez un point pour
chaque question à laquelle vous aurez correctement répondu.
Questions de cours :
Soit 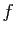 une fonction de
une fonction de
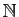 dans
dans
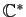 . Pour tout
. Pour tout
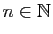 , on
note :
, on
note :
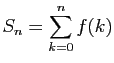
et
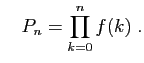
- Soient
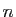 et
et 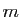 deux entiers tels que
deux entiers tels que 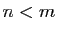 . Exprimer à l'aide de
. Exprimer à l'aide de
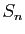 et
et 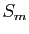 la somme
la somme
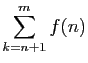 .
Exprimer à l'aide de
.
Exprimer à l'aide de
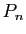 et
et 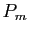 le produit
le produit
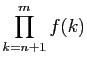 .
.
- Soient
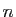 et
et 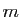 deux entiers tels que
deux entiers tels que
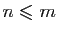 . Montrer que
pour tout complexe
. Montrer que
pour tout complexe  différent de
différent de 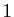 :
:
- Soit
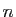 un entier naturel. Montrer que :
un entier naturel. Montrer que :
- En déduire que, pour tout réel positif ou nul
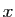 :
:
- Soient
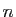 et
et 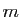 deux entiers tels que
deux entiers tels que
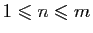 . Montrer que :
. Montrer que :
Exercice 1 :
Soit 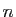 un entier strictement positif.
un entier strictement positif.
- Montrer que :
- En déduire que :
- En déduire que :
- Redémontrer le résultat de la question précédente,
par récurrence sur
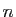 .
.
Exercice 2 :
Soit 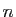 un entier naturel et
un entier naturel et 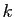 un entier strictement positif. On
appelle partition de
un entier strictement positif. On
appelle partition de 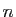 en
en 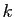 entiers un
entiers un 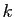 -uplet d'entiers
-uplet d'entiers
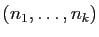 tels que
tels que
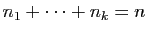 . Par exemple,
. Par exemple,
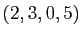 est une partition de
est une partition de 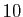 en
en 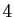 entiers et
entiers et 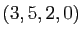 en
est une autre, différente de la précédente. On note
en
est une autre, différente de la précédente. On note
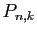 le nombre de partitions de
le nombre de partitions de 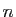 en
en 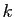 entiers.
entiers.
- En énumérant tous les cas possibles,
montrer que pour tout
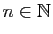 et pour tout
et pour tout
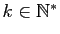 :
:
- Montrer qu'il y a
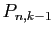 partitions de
partitions de 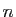 en
en 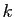 entiers
entiers
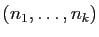 , qui sont telles que
, qui sont telles que 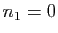 . Montrer qu'il y en a
. Montrer qu'il y en a
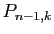 qui sont telles que
qui sont telles que 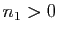 . En
déduire que :
. En
déduire que :
- En déduire que pour tout
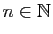 et pour tout
et pour tout
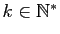 :
:
- On considère
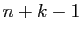 étiquettes alignées sur une table.
On en choisit
étiquettes alignées sur une table.
On en choisit 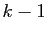 sur lesquelles on écrit le mot
«barrière». Sur les
sur lesquelles on écrit le mot
«barrière». Sur les 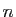 autres, on écrit le mot «unité». Une fois ce choix
effectué, on note :
autres, on écrit le mot «unité». Une fois ce choix
effectué, on note :
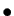
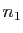 le nombre d'unités à gauche de la première
barrière,
le nombre d'unités à gauche de la première
barrière,
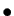
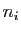 le nombre d'unités entre la
le nombre d'unités entre la
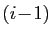 -ième et la
-ième et la 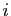 -ième barrière, pour
-ième barrière, pour
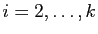 ,
,
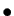
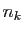 le nombre d'unités à droite de la
le nombre d'unités à droite de la 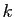 -ième
barrière.
-ième
barrière.
Vérifier que
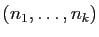 est une partition de
est une partition de 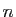 en
en 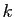 entiers. Réciproquement, vérifier qu'à chaque partition de
entiers. Réciproquement, vérifier qu'à chaque partition de 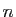 en
en 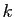 entiers, on peut associer un choix de
entiers, on peut associer un choix de 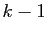 objets parmi
objets parmi
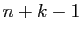 , et un seul. Retrouver le résultat de la question précédente.
, et un seul. Retrouver le résultat de la question précédente.
Exercice 3 :
- Déterminer les racines carrées de
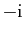 dans
dans
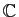 ,
sous forme exponentielle (
,
sous forme exponentielle (
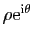 ) et sous forme
algébrique (
) et sous forme
algébrique (
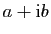 ). (On rappelle que les racines carrées de
). (On rappelle que les racines carrées de
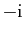 sont les nombres complexes
sont les nombres complexes  tels que
tels que
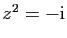 ).
).
- Soit
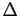 le nombre complexe
le nombre complexe
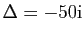 . Déterminer les
racines carrées de
. Déterminer les
racines carrées de 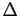 dans
dans
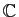 , sous forme algébrique.
, sous forme algébrique.
- Déterminer, sous forme algébrique,
les deux solutions complexes de l'équation :
- Soit
 le point du plan complexe d'affixe
le point du plan complexe d'affixe
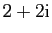 . Soient
. Soient 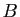 et
et
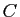 les points du plan complexe ayant pour affixes les solutions
calculées à la question précédente.
Représenter les trois
points
les points du plan complexe ayant pour affixes les solutions
calculées à la question précédente.
Représenter les trois
points 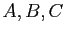 dans le plan complexe.
Démontrer que le triangle
dans le plan complexe.
Démontrer que le triangle
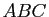 est rectangle en
est rectangle en 
- Soit
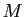 le milieu du segment
le milieu du segment ![$ [B,C]$](img550.gif) , et
, et 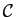 le cercle de
centre
le cercle de
centre 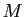 et de rayon
et de rayon
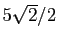 . Montrer que les trois points
. Montrer que les trois points
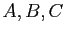 appartiennent au cercle
appartiennent au cercle 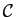 .
.
- Soit
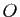 l'origine du plan complexe. Calculer les affixes des images de
l'origine du plan complexe. Calculer les affixes des images de
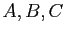 par la rotation de centre
par la rotation de centre 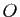 et d'angle
et d'angle  .
.
- Calculer les affixes des images de
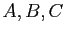 par l'homothétie de centre
par l'homothétie de centre 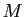 et de rapport
et de rapport 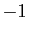 .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() une fonction de
une fonction de
![]() dans
dans
![]() . Pour tout
. Pour tout
![]() , on
note :
, on
note :
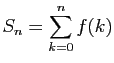 et
et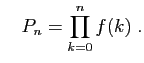
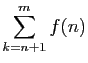 .
Exprimer à l'aide de
.
Exprimer à l'aide de
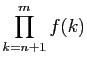 .
.
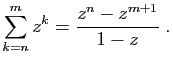
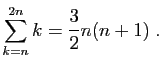
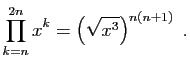
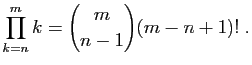
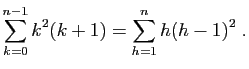
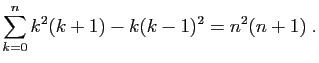
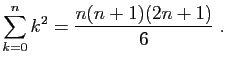
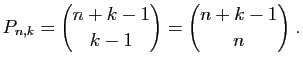
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales