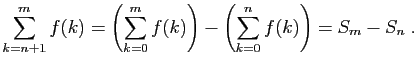
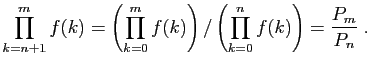
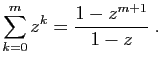
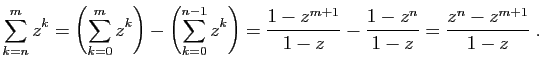
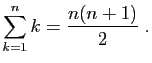
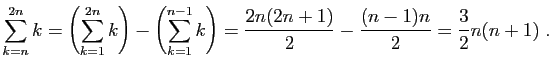
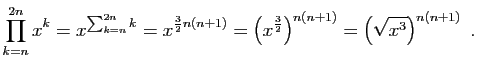
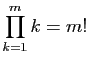 et
et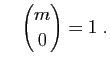
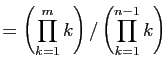 |
|||
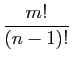 |
|||
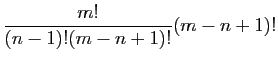 |
|||
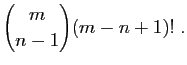 |
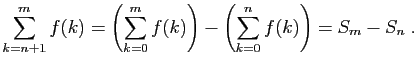
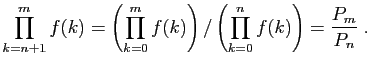
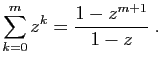
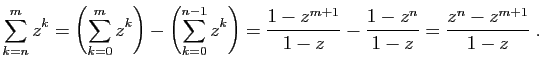
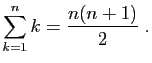
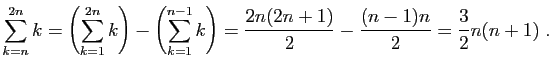
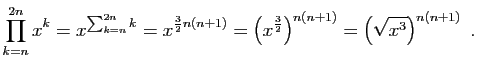
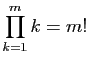 et
et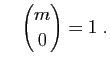
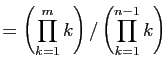 |
|||
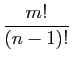 |
|||
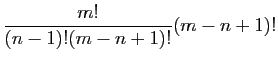 |
|||
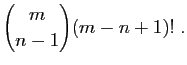 |
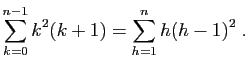
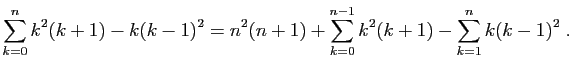
 |
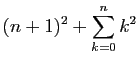 |
||
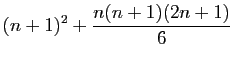 |
|||
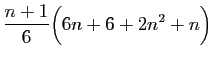 |
|||
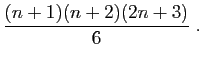 |
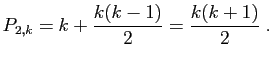
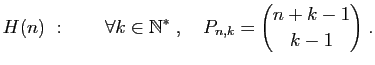
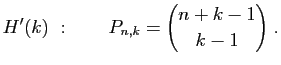
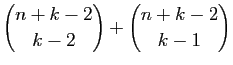 |
|||
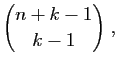 |
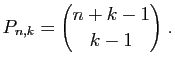
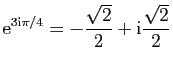 et
et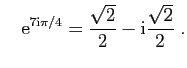
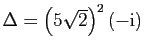 . Ses racines carrées sont
celles de
. Ses racines carrées sont
celles de
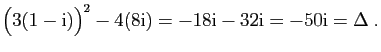
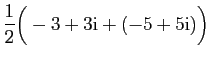 et
et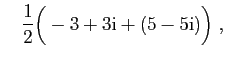
Soient
![]() les affixes respectives des points
les affixes respectives des points ![]() .
.
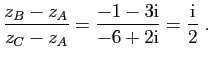
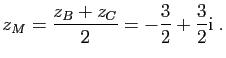
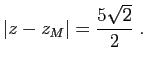
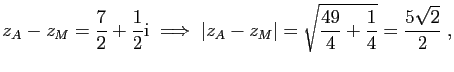
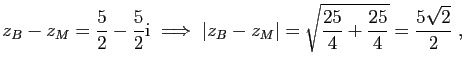
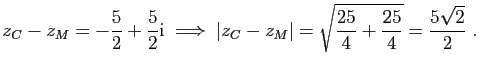
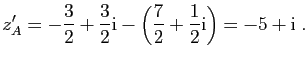
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales