-
-
 .
.
-
-
 .
.
-
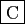
-
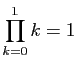 .
.
-
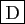
-
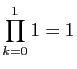 .
.
-
-
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
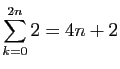 .
.
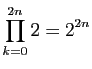 .
.
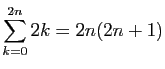 .
.
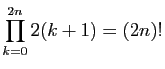 .
.
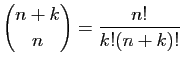 .
.
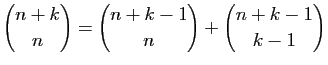 .
.
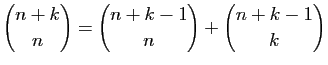 .
.
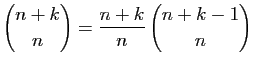 .
.
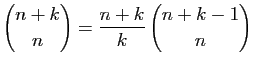 .
.
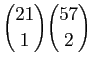 chiens différents
contenant au moins un atout.
chiens différents
contenant au moins un atout.
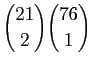 chiens différents
contenant au moins deux atouts.
chiens différents
contenant au moins deux atouts.
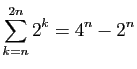 .
.
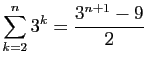 .
.
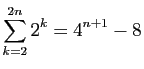 .
.
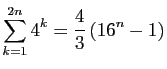 .
.
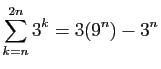 .
.
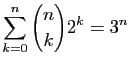 .
.
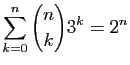 .
.
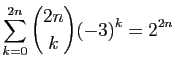 .
.
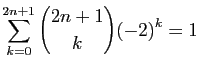 .
.
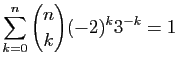 .
.
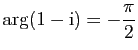 .
.
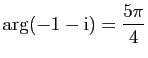 .
.
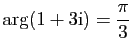 .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales