Exercice 1
Calculer les nombres suivants.
Exercice 2
Soient
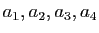 quatre variables. Ecrire à l'aide des
symboles
quatre variables. Ecrire à l'aide des
symboles 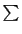 et
et 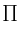 les quantités suivantes.
les quantités suivantes.
-
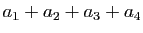 .
.
-
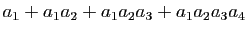 .
.
-
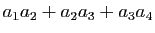 .
.
-
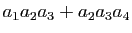 .
.
-
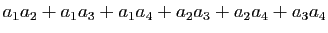 .
.
-
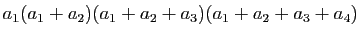 .
.
Exercice 3
Démontrer les égalités suivantes.
-
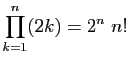 .
.
-
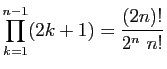 .
.
-
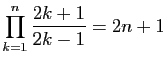 .
.
-
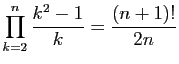 .
.
Exercice 4
Une entreprise veut se donner un nouveau sigle, qui soit formé
d'exactement 3 lettres. De combien de façons peut-elle le faire ?
Combien reste-t-il de possibilités si on impose au sigle d'être
formé de lettres distinctes ?
Exercice 5
On met dans une boîte 26 jetons de Scrabble, portant chacune des
lettres de l'alphabet. On en tire 3 à la fois. Combien de tirages
différents peut-on obtenir ?
Exercice 6
Dix personnes doivent s'asseoir autour d'une table circulaire. On
considère comme identiques deux dispositions dont l'une se déduit
de l'autre par une rotation. Combien y a-t-il de dispositions
possibles ? Combien en reste-t-il si deux personnes données refusent
d'être assises à côté ?
Exercice 7
Une association comprenant 20 membres dont 12 femmes et 8 hommes
désire former un comité de 5 personnes, dans lequel doivent se
trouver au moins deux hommes et deux femmes. Calculer de combien de
façons on peut former ce comité dans chacun des cas suivants.
- Chaque membre de l'association accepte d'en faire partie.
- Deux des femmes refusent d'en faire partie.
- Monsieur X et Madame Y refusent de siéger ensemble.
Exercice 8
Démontrer les égalités suivantes.
-
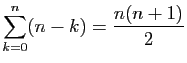 .
.
-
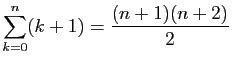 .
.
-
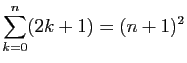 .
.
Exercice 9
Démontrer les égalités suivantes.
-
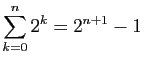 .
.
-
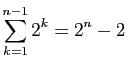 .
.
-
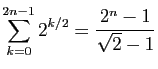 .
.
-
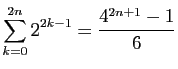 .
.
-
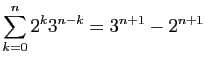 .
.
-
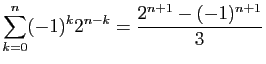 .
.
Exercice 10
Démontrer les égalités suivantes.
-
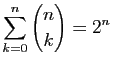 .
.
-
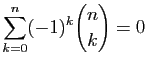 .
.
-
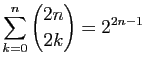 (ajoutez les deux égalités précédentes).
(ajoutez les deux égalités précédentes).
-
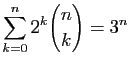 .
.
-
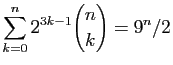 .
.
-
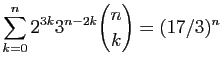 .
.
-
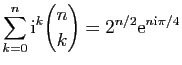 .
.
-
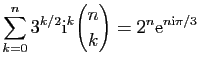 .
.
-
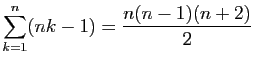 .
.
Exercice 11
Calculer les sommes suivantes.
-
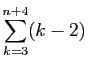 .
.
-
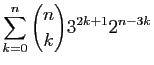 .
.
Exercice 15
Mettre sous la forme
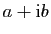 les nombres complexes suivants.
les nombres complexes suivants.
Exercice 16
Calculer le module et l'argument des nombres complexes suivants.
Exercice 17
Mettre sous la forme
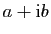 les nombres complexes suivants.
les nombres complexes suivants.
Exercice 18
Effectuer les calculs suivants en utilisant la forme
exponentielle.
Exercice 19
Calculer les racines carrées des nombres suivants.
Exercice 20
- Calculer les racines carrées de
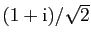 . En déduire les
valeurs de
. En déduire les
valeurs de
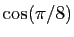 et
et
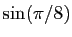 .
.
- Calculer les racines carrées de
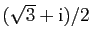 . En déduire les
valeurs de
. En déduire les
valeurs de
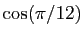 et
et
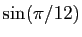 .
.
Exercice 21
Résoudre dans
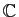 les équations suivantes.
les équations suivantes.
Exercice 22
Soit 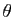 un réel.
un réel.
- Calculer la somme
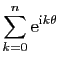 . En déduire les valeurs de
. En déduire les valeurs de
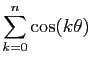 et
et
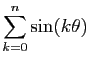 .
.
- Calculer la somme
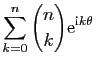 .
En déduire les valeurs de
.
En déduire les valeurs de
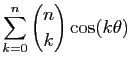 et
et
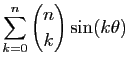 .
.
Exercice 24
- Déterminer l'ensemble des complexes
 tels que
tels que
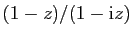 soit
réel.
soit
réel.
- Déterminer l'ensemble des complexes
 tels que
tels que
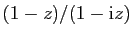 soit
imaginaire pur.
soit
imaginaire pur.
- Déterminer l'ensemble des complexes
 tels que les points d'affixe
tels que les points d'affixe
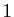 ,
,  ,
, 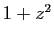 soient alignés.
soient alignés.
- Déterminer l'ensemble des complexes
 tels que les points d'affixe
tels que les points d'affixe
 ,
,
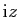 ,
,
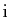 forment un triangle équilatéral.
forment un triangle équilatéral.
- Déterminer l'ensemble des complexes
 tels que les points d'affixe
tels que les points d'affixe
 ,
, 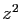 ,
, 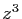 forment un triangle rectangle au point d'affixe
forment un triangle rectangle au point d'affixe  .
.
- Déterminer l'ensemble des complexes
 tels que les points d'affixe
tels que les points d'affixe
 ,
, 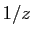 ,
, 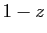 soient sur un même cercle, de centre l'origine.
soient sur un même cercle, de centre l'origine.
Exercice 25
- Montrer que
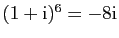 .
.
- En déduire une solution de l'équation
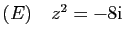 .
.
- Ecrire les deux solutions de
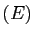 sous forme algébrique,
et sous forme exponentielle.
sous forme algébrique,
et sous forme exponentielle.
- Déduire de la première question une solution de l'équation
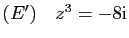 .
.
- Soit
 le point d'affixe
le point d'affixe
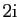 . Soit
. Soit 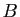 l'image de
l'image de  par la
rotation de centre
par la
rotation de centre 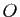 et d'angle
et d'angle 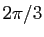 . Soit
. Soit 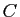 l'image de
l'image de 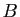 par
la même rotation. Ecrire les affixes des points
par
la même rotation. Ecrire les affixes des points 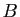 et
et 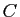 , sous
forme exponentielle, puis sous forme algébrique.
, sous
forme exponentielle, puis sous forme algébrique.
- Vérifier que les affixes calculées à la question
précédente sont solution de
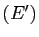 .
.
- Montrer que le triangle
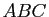 est équilatéral et que
est équilatéral et que 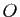 est
son centre de gravité.
est
son centre de gravité.
Exercice 26
On note 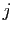 le nombre complexe
le nombre complexe
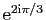 . On pose
. On pose 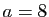 ,
, 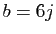 et
et
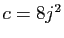 . On note
. On note  ,
, 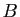 et
et 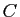 les points d'affixes respectives
les points d'affixes respectives 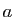 ,
,
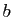 et
et 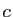 . On note
. On note
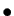
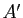 l'image de
l'image de 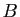 par la rotation de centre
par la rotation de centre 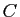 ,
et d'angle
,
et d'angle 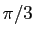
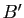 l'image de
l'image de 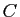 par la rotation de centre
par la rotation de centre  ,
et d'angle
,
et d'angle 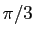
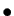
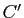 l'image de
l'image de  par la rotation de centre
par la rotation de centre 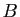 .
et d'angle
.
et d'angle 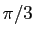
On note 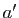 ,
, 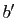 et
et 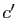 les affixes respectives de
les affixes respectives de 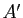 ,
, 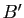 et
et 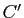 .
.
- Calculer
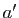 ,
, 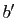 et
et 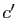 .
.
- Montrer que les droites
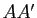 ,
, 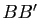 et
et 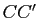 sont concourantes
en 0.
sont concourantes
en 0.
- Montrer que
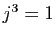 et
et 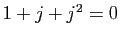
- Soit
 un nombre complexe quelconque. Montrer que
un nombre complexe quelconque. Montrer que
- On admet que quels que soient les nombres complexes
 et
et 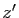 ,
,
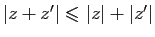 . Montrer que la somme de distances
. Montrer que la somme de distances 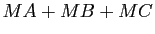 est minimale lorsque
est minimale lorsque 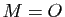 .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
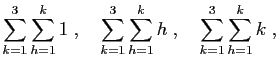
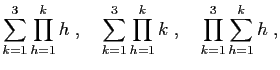
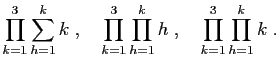
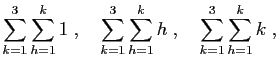
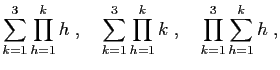
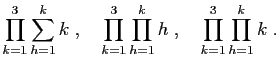
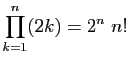 .
.
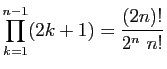 .
.
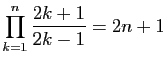 .
.
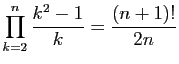 .
.
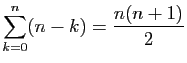 .
.
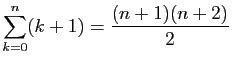 .
.
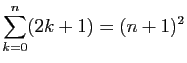 .
.
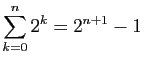 .
.
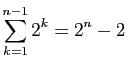 .
.
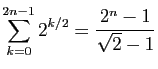 .
.
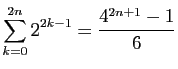 .
.
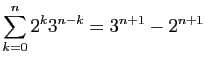 .
.
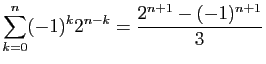 .
.
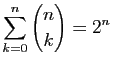 .
.
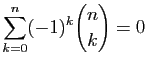 .
.
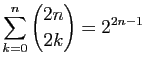 (ajoutez les deux égalités précédentes).
(ajoutez les deux égalités précédentes).
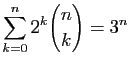 .
.
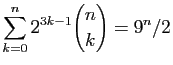 .
.
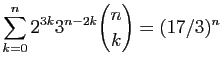 .
.
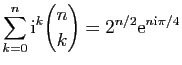 .
.
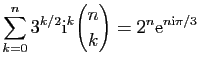 .
.
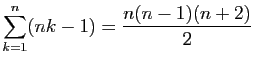 .
.
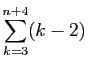 .
.
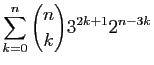 .
.
![$\displaystyle \int_{0}^1f(x)dx=\left[\frac{(1+x)^{n+1}}{n+1}\right]_{0}^1=\frac{2^{n+1}-1}{n+1}.$](img355.gif)
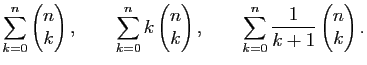
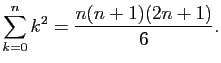
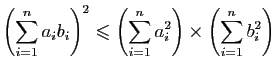
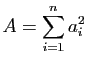 ,
,
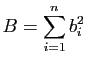 ,
,
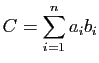 .
.
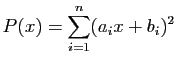 . Exprimez
. Exprimez 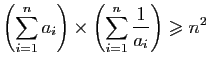
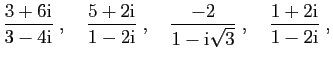
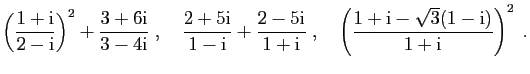
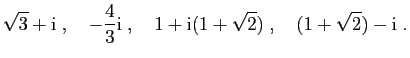
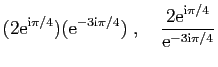
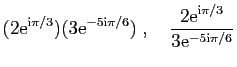
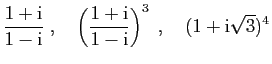
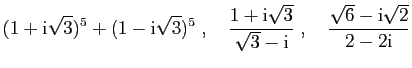
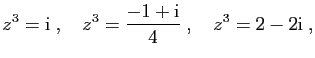
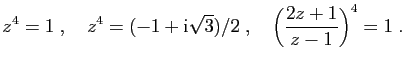
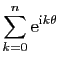 . En déduire les valeurs de
. En déduire les valeurs de
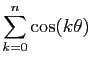 et
et
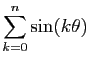 .
.
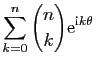 .
En déduire les valeurs de
.
En déduire les valeurs de
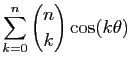 et
et
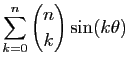 .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales