
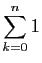 .
.
-
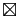
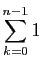 .
.

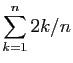 .
.
-
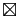
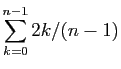 .
.
-
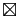
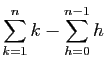 .
.

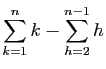 .
.
-
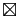
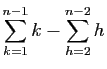 .
.

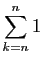 .
.
-
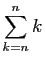 .
.
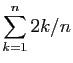 .
.
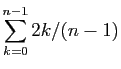 .
.
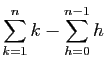 .
.
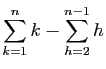 .
.
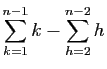 .
.
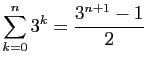 .
.
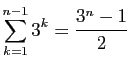 .
.
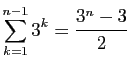 .
.
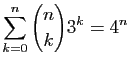 .
.
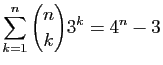 .
.
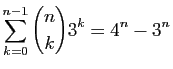 .
.
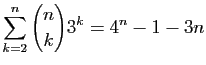 .
.
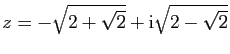 .
Parmi les affirmations suivantes, lesquelles sont
vraies, lesquelles sont fausses et pourquoi ?
.
Parmi les affirmations suivantes, lesquelles sont
vraies, lesquelles sont fausses et pourquoi ?
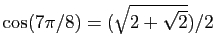 .
.
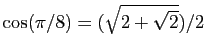 .
.
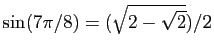 .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales