- Montrer que
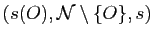 est un triplet
naturel.
est un triplet
naturel.
- On note
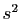 l'application composée
l'application composée 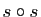 . Soit
. Soit
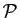 une
propriété définie sur
une
propriété définie sur
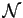 telle que
telle que
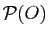 est vraie,
est vraie,
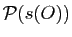 fausse et :
On note
fausse et :
On note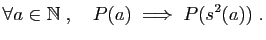
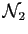 l'ensemble des éléments de
l'ensemble des éléments de
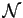 tels que
tels que
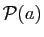 est vraie. Montrer que
est vraie. Montrer que
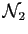 est un
ensemble non majoré.
est un
ensemble non majoré.
- Montrer que
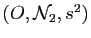 est un triplet naturel.
est un triplet naturel.
- On note
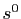 l'application identique, et on définit par récurrence
l'application identique, et on définit par récurrence
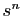 comme l'application composée
comme l'application composée
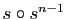 , pour
, pour
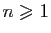 . Définir l'application
successeur
. Définir l'application
successeur 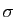 telle que
telle que
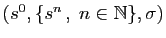 soit
un triplet naturel.
soit
un triplet naturel.
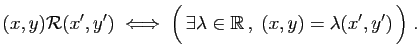
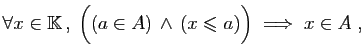
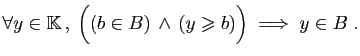
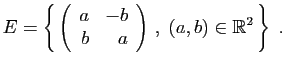
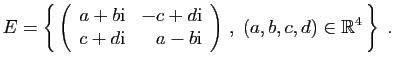
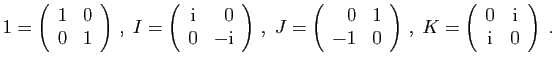
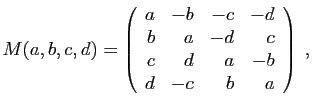
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales