Section : Cours
Avant : PGCD et PPCM
Après : Sous-groupes de

Lemme de Gauss et décomposition en facteurs premiers

Le lemme de Gauss permet de démontrer l'unicité de la décomposition en facteurs premiers. Ce dernier résultat semble plus facile d'usage pour un utilisateur peu expérimenté, donc on énonce le lemme de Gauss sans commentaire, ou plus exactement sans autre commentaire que ce commentaire négatif.

Lemme 1   Soit $ a$, $ b$ et $ c$ trois entiers strictement positifs. Si $ a$ divise le produit $ bc$ et si $ a$ est premier avec $ c$, alors $ a$ divise $ b$.

Démonstration : Puisque $ a$ est premier avec $ c$, le pgcd de $ a$ et $ c$ est $ 1$, donc il existe des entiers relatifs $ s$ et $ t$ tels que $ sa+tc=1$. Multiplions cette identité par $ b$ : on obtient $ b=asb+tbc$. Mais dans cette écriture, $ asb$ est évidemment multiple de $ a$ tandis que $ tbc$ l'est parce que $ bc$ est multiple de $ a$. On en déduit que $ b$, somme des deux multiples de $ a$ que sont $ asb$ et $ tbc$, est lui-même un multiple de $ a$.$ \square$

Théorème (énoncé approximatif) Tout entier $ n\geqslant 2$ peut être écrit de façon unique comme produit de facteurs premiers.


L'énoncé est approximatif car il n'est pas si clair de savoir ce que signifie «unique» : on peut écrire $ 6=2\times 3=3\times 2$ mais il faut évidemment considérer que c'est la même chose. Pour pouvoir comprendre voire utiliser le théorème, cet énoncé suffira bien ; mais pour le démontrer, il faut être plus précis.

Théorème 5 (énoncé précis)   Tout entier $ n\geqslant 2$ peut être écrit comme produit de facteurs premiers. De plus, si on dispose de deux écritures

$\displaystyle n=p_1^{\alpha_1}p_2^{\alpha_2}\cdots p_k^{\alpha_k}$   et$\displaystyle \qquad n=q_1^{\beta_1}q_2^{\beta_2}\cdots q_i^{\beta_i}, $

dans lesquelles $ k\geqslant 1$, $ i\geqslant 1$, les entiers $ p_1<p_2<\ldots<p_k$ et $ q_1<q_2<\ldots<q_i$ sont tous premiers et rangés en ordre croissant, les exposants $ \alpha_1$, $ \alpha_2$, ..., $ \alpha_k$ et $ \beta_1$, $ \beta_2$, ..., $ \beta_i$ sont tous des entiers strictement positifs, alors ces deux écritures sont les mêmes au sens précis suivant : $ k=i$ et pour tout $ j$ avec $ 1\leqslant j\leqslant k=i$, $ p_j=q_j$ et $ \alpha_j=\beta_j$.

Démonstration : À énoncé indigeste, démonstration indigeste.

L'existence provient d'une récurrence élémentaire. Pour tout entier $ n\ge2$, considérons l'hypothèse de récurrence (forte) suivante :

$ (E_{n})$ Tout entier $ 2\leqslant k\leqslant n$ peut s'écrire comme un produit de facteurs premiers comme dans l'énoncé du théorème.

Alors $ (E_{2})$ est évidente car $ 2$ est premier.

Soit $ n\ge2$ un entier fixé, supposons $ (E_{n})$ vraie et montrons $ (E_{n+1})$.

Si $ n+1$ est premier, $ (E_{n+1})$ est évidente.

Si $ n+1$ n'est pas premier, il existe un entier $ 2\leqslant k\leqslant n$ qui divise $ n+1$. Notons $ \ell$ l'entier $ \ell=(n+1)/k$. Alors $ 2\leqslant \ell\leqslant n$ donc on peut appliquer l'hypothèse $ (E_{n})$ aux deux entiers $ k$ et $ \ell$. Il existe donc des entiers premiers $ p_{i}$ et $ q_{j}$ et des exposants $ a_{i}$ et $ b_{j}$ strictement positifs tels que

$\displaystyle k=p_{1}^{a_{1}}p_{2}^{a_{2}}\cdots p_{u}^{a_{u}},\qquad \ell=q_{1}^{b_{1}}q_{2}^{b_{2}}\cdots q_{v}^{b_{v}}, $

avec $ p_1<p_2<\ldots<p_u$ et $ q_1<q_2<\ldots<q_v$. Par conséquent,

$\displaystyle n+1=k\times\ell=p_{1}^{a_{1}}p_{2}^{a_{2}}\cdots p_{u}^{a_{u}}\times q_{1}^{b_{1}}q_{2}^{b_{2}}\cdots q_{v}^{b_{v}}. $

L'ensemble $ \{p_{1},p_{2},\ldots,p_{u}\}\cup\{q_{1},q_{2},\ldots,q_{v}\}$ comporte $ w\leqslant u+v$ éléments. Notons et ordonnons ces éléments comme $ r_{1}<r_{2}<\cdots<r_{w}$. En regroupant les entiers qui apparaissent dans les deux factorisations, on obtient

$\displaystyle n+1=r_{1}^{c_{1}}r_{2}^{c_{2}}\cdots r_{w}^{c_{w}}, $

où les exposants $ c_{k}$ sont définis comme suit : Donc $ (E_{n+1})$ est vraie.

Ceci conclut la preuve de l'existence.


Passons à l'unicité. On va donc montrer par récurrence (forte) sur $ n$ le résultat d'unicité $ (H_n)$ écrit dans l'énoncé du théorème.


Démonstration de $ (H_2)$, et en fait même de $ (H_p)$ pour tout nombre premier $ p$


Supposons $ n=p$ premier écrit sous forme de produit $ p=p_1^{\alpha_1}p_2^{\alpha_2}\cdots p_k^{\alpha_k}$. Chaque $ p_i$ est un diviseur positif de $ p$ non égal à $ 1$, donc chaque $ p_i$ est égal à $ p$. Ceci entraîne aussitôt que $ k=1$ et que $ \alpha_1=1$ (sans cela le produit serait supérieur ou égal à $ p^2$ donc distinct de $ p$). L'écriture $ p=p$ est donc la seule possible pour $ p$, ce qui démontre $ (H_{p})$ quand $ p$ est premier.


Soit maintenant $ n$ un entier fixé, non premier, avec $ n>2$, et supposons l'hypothèse d'unicité $ (H_m)$ prouvée pour tout entier $ m$ avec $ 2\leqslant m <n$.


Première étape Montrons que $ p_k=q_i$ (toujours dans les notations de l'énoncé du théorème).

Supposons tout d'abord que $ p_k>q_i$ et montrons que l'on aboutit à une absurdité.

Puisque les $ q_j$ sont supposés rangés dans l'ordre croissant, $ p_k$ est alors forcément distinct de tous les $ q_j$ ; $ p_k$ et chaque $ q_j$ étant premiers, on en conclut que leur seul diviseur commun positif est $ 1$ : $ p_k$ et $ q_j$ sont donc premiers entre eux.

Fixons un $ j$ entre $ 1$ et $ i$ et montrons par récurrence sur $ b\geqslant 0$ l'énoncé fort intuitif suivant : $ (H'_b)$ : $ p_k$ est premier avec $ q_j^b$.


$ (H'_0)$ est évident puisque $ q_{j}^{0}=1$.

Soit $ b\geqslant 0$ un entier fixé, supposons $ (H'_b)$ vrai et montrons $ (H'_{b+1})$.

Si $ (H'_{b+1})$ était faux, le pgcd de $ p_k$ et $ q_j^{b+1}$ ne serait pas $ 1$ ; comme c'est un diviseur positif de $ p_k$, ce serait $ p_k$ qui diviserait donc $ q_j^{b+1}$. On peut alors appliquer le lemme de Gauss : comme $ p_k$ divise $ q_j^{b+1}=q_j^bq_j$ et que $ p_k$ est premier avec $ q_j$, $ p_k$ divise $ q_j^b$. Mais ceci contredit l'hypothèse $ (H'_b)$. L'hypothèse $ (H'_{b+1})$ est donc vraie.


On a donc bien montré que pour tout $ b\geqslant 0$, $ p_k$ est premier avec $ q_j^b$. En particulier, $ p_k$ est premier avec $ q_j^{\beta_j}$. Comme on a prouvé cette affirmation pour un $ j$ quelconque, on a prouvé que pour tout $ j$ entre $ 1$ et $ i$, $ p_k$ est premier avec $ q_j^{\beta_j}$. Ce qu'on a fait avec les puissances de chaque $ q_j$, on va maintenant le recommencer avec le produit de ces puissances. Précisément, on va montrer par récurrence sur l'entier $ j$ que pour tout $ j$ avec $ 1\leqslant j\leqslant l$, on a l'énoncé $ (H''_j)$ : $ p_k$ est premier avec $ q_1^{\beta_1}q_2^{\beta_2}\cdots q_j^{\beta_j}$.


Les lecteurs encore éveillés (s'il en reste) comprendront que la preuve est à peu près la même que celle des $ (H'_b)$, pour les autres, la voilà :

Pour $ j=1$, on doit prouver que $ p_k$ est premier avec $ q_1^{\beta_1}$. C'est déjà fait.

Fixons un entier $ j$ avec $ 1\leqslant j<i$ et supposons l'hypothèse $ (H''_j)$ vraie.

Si $ (H''_{j+1})$ était fausse, le pgcd de $ p_k$ et $ q_1^{\beta_1}q_2^{\beta_2}\cdots q_j^{\beta_j}q_{j+1}^{\beta_{j+1}}$ ne serait pas $ 1$ ; comme c'est un diviseur positif de $ p_k$, ce serait $ p_k$ qui diviserait donc $ q_1^{\beta_1}q_2^{\beta_2}\cdots q_j^{\beta_j}q_{j+1}^{\beta_{j+1}}$. On peut alors appliquer le lemme de Gauss : comme $ p_k$ divise le nombre

$\displaystyle q_1^{\beta_1}q_2^{\beta_2}\cdots q_j^{\beta_j}q_{j+1}^{\beta_{j+1... ...eft(q_1^{\beta_1}q_2^{\beta_2}\cdots q_j^{\beta_j}\right)q_{j+1}^{\beta_{j+1}} $

et comme $ p_k$ est premier avec $ q_{j+1}^{\beta_{j+1}}$, $ p_k$ divise $ q_1^{\beta_1}q_2^{\beta_2}\cdots q_j^{\beta_j}$. Mais ceci contredit l'hypothèse $ (H''_j)$. L'hypothèse $ (H''_{j+1})$ est donc vraie.


On a donc montré $ (H''_j)$ pour tout $ j$ entre $ 1$ et $ i$ ; en particulier on a montré $ (H''_i)$, à savoir que $ p_k$ est premier avec $ q_1^{\beta_1}q_2^{\beta_2}\cdots q_i^{\beta_i}=n$. Mais pourtant $ p_k$ figure dans l'autre décomposition en facteurs premiers de $ n$ (ce n'est pas une illusion d'optique, puisqu'on a pris soin de supposer $ \alpha_k\geqslant 1$), donc $ p_k$ divise $ n$. D'où contradiction. Ouf !


On ne peut donc avoir $ p_k>q_i$. En échangeant les rôles des coefficients $ p$ et $ q$, on voit qu'on ne peut pas non plus avoir $ q_i>p_k$. On en déduit donc que $ q_i=p_k$.

Fin de la première étape


Deuxième étape On va profiter de ce tout petit morceau d'égalité pour arriver à utiliser l'hypothèse de récurrence et faire tomber toutes les autres égalités requises en cascade.


Notons $ N=n/p_k=n/q_i$, on a ainsi :

$\displaystyle N=p_1^{\alpha_1}p_2^{\alpha_2}\cdots p_k^{\alpha_k-1}\qquad{\rm et}\qquad N=q_1^{\beta_1}q_2^{\beta_2}\cdots q_i^{\beta_i-1}. $

De plus $ N$ est strictement inférieur à $ n$, et $ N$ est strictement plus grand que $ 1$ car on a fort opportunément supposé $ n$ non premier. On va donc appliquer l'hypothèse de récurrence $ (H_N)$ à ces deux écritures de $ N$ en facteurs premiers. Si on n'est pas méticuleux, on oubliera de s'assurer que tous les exposants sont strictements positifs, et on aura fini tout de suite ; ce sera faux, mais de peu. Hélas, un enseignant scrupuleux ne peut se le permettre et doit donc veiller à ce petit détail, qui nous force à distinguer deux sous-cas.


Premier sous-cas : $ \alpha_k=1$. Dans ce cas, la première écriture de $ m$ se lit en réalité, après effacement du $ p_k^0$ qui l'encombre :

$\displaystyle N=p_1^{\alpha_1}p_2^{\alpha_2}\cdots p_{k-1}^{\alpha_{k-1}}. $

Ainsi $ N$ possède une décomposition en facteurs premiers dans laquelle $ p_k$ ne figure pas. Comme sa décomposition est unique, $ p_k$ ne peut non plus figurer dans l'autre décomposition, et comme $ q_i=p_k$, la seule possibilité est que l'exposant $ \beta_i-1$ soit nul ; ainsi $ \beta_i=\alpha_k$ =1, et les deux représentations

$\displaystyle N=p_1^{\alpha_1}p_2^{\alpha_2}\cdots p_{k-1}^{\alpha_{k-1}}$   et$\displaystyle \quad N=q_1^{\beta_1}q_2^{\beta_2}\cdots q_{i-1}^{\beta_{i-1}} $

sont deux décompositions de $ N$ en facteurs premiers. On en déduit que $ k-1=i-1$, donc $ k=i$, puis l'égalité de tous les facteurs premiers et exposants encore en attente d'élucidation.


Second sous-cas : $ \alpha_k>1$. C'est la même chanson. On remarque tout d'abord qu'on a aussi $ \beta_i>1$ (sans cela, en échangeant les rôles des coefficients $ p$ et $ q$ et en utilisant le premier cas, on montrerait que $ \alpha_k=1$) ; donc les deux décompositions

$\displaystyle N=p_1^{\alpha_1}p_2^{\alpha_2}\cdots p_k^{\alpha_k-1}$   et$\displaystyle \quad N=q_1^{\beta_1}q_2^{\beta_2}\cdots q_i^{\beta_i-1} $

vérifient bien les hypothèses du théorème. Elles sont égales, donc $ k=i$ et chaque coefficient $ p$ est égal au coefficient $ q$ correspondant, avec le même exposant.

Fin de la deuxième étape

$ (H_n)$ est donc prouvée.

La récurrence est donc terminée, et avec elle la démonstration.$ \square$ La décomposition en facteurs premiers permet d'énumérer facilement les diviseurs d'un entier.

Proposition 1   Soit $ n$ un entier et

$\displaystyle n=p_1^{\alpha_1}p_2^{\alpha_2}\cdots p_k^{\alpha_k}$

sa décomposition en facteurs premiers. L'ensemble des diviseurs positifs de $ n$ est :

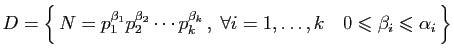
$\displaystyle D=\Big\{ N=p_1^{\beta_1}p_2^{\beta_2}\cdots p_k^{\beta_k} ,\; \forall i=1,\ldots, k\quad 0\leqslant \beta_i\leqslant \alpha_i \Big\} $

Par exemple l'ensemble des diviseurs positifs de $ 60=2^2 3^1 5^1$ est :

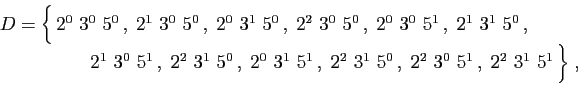
\begin{displaymath} \begin{array}{l} D=\Big\{ 2^0 3^0 5^0 ,\;2^1 3^0 5^0 ,\;... ...3^1 5^0 ,\; 2^2 3^0 5^1 ,\;2^2 3^1 5^1 \Big\}\;, \end{array}\end{displaymath}

soit,

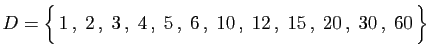
$\displaystyle D=\Big\{ 1 ,\;2 ,\;3 ,\;4 ,\; 5 ,\;6 ,\;10 ,\; 12 ,\;15 ,\;20 ,\;30 ,\;60 \Big\} $

Démonstration : Soit

$\displaystyle n=p_1^{\alpha_1}p_2^{\alpha_2}\cdots p_k^{\alpha_k}$   et$\displaystyle \quad N=p_1^{\beta_1}p_2^{\beta_2}\cdots p_k^{\beta_k} $

Si pour tout $ i=1,\ldots,k$, $ 0\leqslant \beta_i\leqslant \alpha_i$, alors :

$\displaystyle n=N\times\big( p_1^{\alpha_1-\beta_1}p_2^{\alpha_2-\beta_2}\cdots p_k^{\alpha_k-\beta_k} \big) $

Donc tout élément de l'ensemble $ D$ est diviseur de $ n$.

Réciproquement, soit $ N$ un diviseur de $ n$. Tout facteur premier de $ N$ divise $ n$, donc c'est l'un des $ p_i$. Si $ p_i^{\beta_i}$ divise $ N$, alors $ p_i^{\beta_i}$ divise aussi $ n$, donc $ \beta_i\leqslant \alpha_i$. Ceci montre que tout diviseur de $ n$ est élément de $ D$. $ \square$ Quand on connaît la décomposition en facteurs premiers de deux nombres, il est facile de calculer leur pgcd et leur ppcm.

Proposition 2   Soient $ m$ et $ n$ deux entiers. Quitte à admettre des exposants nuls, nous pouvons considérer que leurs facteurs premiers sont les mêmes. Ecrivons donc :

$\displaystyle n=p_1^{\alpha_1}p_2^{\alpha_2}\cdots p_k^{\alpha_k}$   et$\displaystyle \quad m=p_1^{\beta_1}p_2^{\beta_2}\cdots p_k^{\beta_k}\;, $

où pour $ i=1,\ldots,k$, $ \alpha_i\geqslant 0$ et $ \beta_i\geqslant 0$. Alors :

$\displaystyle \mathrm{pgcd}(m,n)=p_1^{\delta_1}p_2^{\delta_2}\cdots p_k^{\delta_k}$   et$\displaystyle \quad \mathrm{ppcm}(m,n)=p_1^{\gamma_1}p_2^{\gamma_2}\cdots p_k^{\gamma_k}\;, $

où pour tout $ i=1,\ldots,k$,

$\displaystyle \delta_i = \min\{\alpha_i,\beta_i\}$   et$\displaystyle \quad \gamma_i = \max\{\alpha_i,\beta_i\} $

Considérons par exemple :

$\displaystyle n=172872=2^3 3^2 7^4$   et$\displaystyle \quad m=525525=3^1 5^2 7^2 11^1 13^1 $

Quitte à admettre des puissances nulles, nous pouvons écrire la décomposition sur les mêmes facteurs.

$\displaystyle n=2^3 3^2 5^0 7^4 11^0 13^0$   et$\displaystyle \quad m=2^0 3^1 5^2 7^2 11^1 13^1 $

Donc :

$\displaystyle \mathrm{pgcd}(m,n)=2^0 3^1 5^0 7^2 11^0 13^0=3^1 7^2=147, $

et

$\displaystyle \mathrm{ppcm}(m,n)=2^3 3^2 5^2 7^4 11^1 13^1=618017400. $

Démonstration : Posons :

$\displaystyle d=p_1^{\delta_1}p_2^{\delta_2}\cdots p_k^{\delta_k}. $

On vérifie facilement que $ d$ est bien un diviseur commun de $ m$ et de $ n$. Réciproquement, soit $ d'$ un diviseur commun de $ m$ et $ n$. Tout facteur premier $ p$ de $ d$ est aussi un facteur premier de $ m$ et de $ n$. Si $ p_i^\delta$ divise $ n$ et $ m$, alors $ \delta\leqslant \alpha_i$ et $ \delta\leqslant \beta_i$, donc

$\displaystyle \delta\leqslant \delta_i=\min\{\alpha_i,\beta_i\}. $

Ceci entraîne que $ d'$ est diviseur de $ d$. Donc $ d$ est bien le pgcd de $ m$ et $ n$. L'expression du ppcm se déduit de celle du pgcd par la formule :

$\displaystyle \mathrm{pgcd}(m,n) \mathrm{ppcm}(m,n) = m n. $

$ \square$

Section : Cours
Avant : PGCD et PPCM
Après : Sous-groupes de


         © UJF Grenoble, 2011                              Mentions légales