- Démontrer que si
 n'est divisible par aucun entier inférieur ou
égal à
n'est divisible par aucun entier inférieur ou
égal à 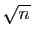 , alors
, alors  est premier.
est premier.
- Démontrer que les nombres
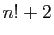 ,
, 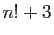 ,...,
,..., 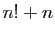 ne
sont pas premiers.
ne
sont pas premiers.
- En déduire que pour tout
 , il existe
, il existe  entiers consécutifs
non premiers.
entiers consécutifs
non premiers.
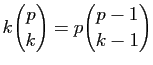
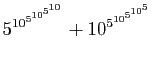
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales