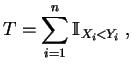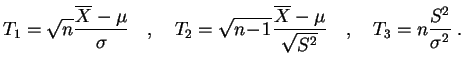Sección : Tests Estadísticos
Previo : Función potencia
Siguiente : Índice
NB: En los ejercicios que siguen, los valores
propuestos para los tamaños de las muestras así como para los
parámetros de las leyes, son solamente indicativos. Pueden ser
variados en función de la potencia de cálculo disponible.
Ejercicio 1
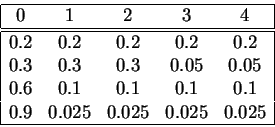
Para cada una de las siguientes leyes (
) :

- ley binomial
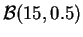 ,
,
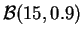 ,
,
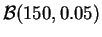 .
.

- ley de Poisson
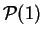 ,
,
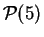 .
.

- ley geométrica
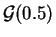 ,
,
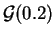 .
.
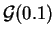 .
.

- ley exponencial
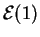 ,
,
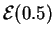 ,
,
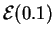 .
.

- ley normal
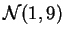 ,
,
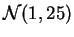 ,
,
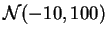 .
.

- ley gamma
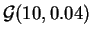 ,
,
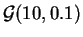 ,
,
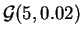 .
.

- ley de chi-cuadrado
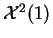 ,
,
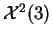 .
.

- ley de Student
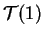 ,
,
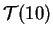 .
.

- ley de Fisher
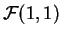 ,
,
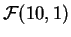 ,
,
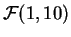 .
.
- Representar gráficamente el diagrama de barras (leyes
discretas) o la densidad (leyes continuas).
- Un estadígrafo
de test
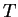 toma el valor
toma el valor 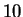 . ¿Que decisión toma usted con
umbral
. ¿Que decisión toma usted con
umbral
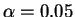 para un test unilateral a la derecha, si la
ley de
para un test unilateral a la derecha, si la
ley de 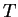 bajo
bajo
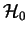 es
es 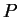 ?.
?.
- Para el mismo test,
calcular el p-valor correspondiente a
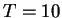 .
.
- Retomar los
incisos precedentes para el test bilateral de umbral
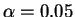 .
.
Ejercicio 2
Para las leyes
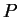
que siguen:

- leyes binomiales
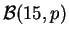 ,
, 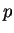 varía de
0 a 1.
varía de
0 a 1.

- leyes de Poisson
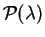 ,
,
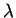 varía de 5 a 10.
varía de 5 a 10.

- leyes geométricas
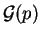 ,
, 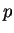 varía de
varía de 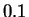 a 1.
a 1.

- leyes
exponenciales
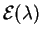 ,
, 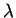 varía de
varía de 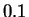 a
a
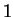 .
.

- ley normal
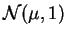 ,
, 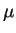 varía
de 5 a 10.
varía
de 5 a 10.

- ley normal
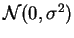 ,
,
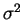 varía de 10 a 100.
varía de 10 a 100.

- ley gamma
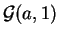 ,
, 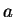 varía de 1 a 10.
varía de 1 a 10.

- ley de
chi-cuadrado
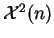 ,
, 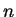 varía de 1 a 10.
varía de 1 a 10.

- ley de Fisher
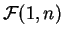 ,
, 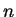 varía de 1
a 10.
varía de 1
a 10.

- ley de Fisher
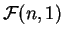 ,
, 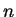 varía
de 1 a 10.
varía
de 1 a 10.
- Para el test unilateral a la derecha basado en un
estadígrafo
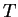 de ley
de ley 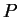 , calcular el p-valor correspondiente
al valor
, calcular el p-valor correspondiente
al valor 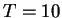 , para valores del parámetro comprendidos en el
intervalo indicado.
, para valores del parámetro comprendidos en el
intervalo indicado.
- Representar gráficamente estos
p-valores.
Ejercicio 13
Simular dos muestras independientes,
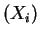
y
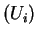
, de la ley
binomial
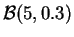
de tamaño
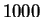
. Sea
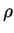
un
número real comprendido estrictamente entre 0 y
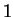
. Sea
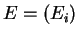
una muestra de la ley de Bernoulli de parámetro
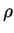
. Se construye la muestra
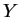
de la siguiente manera: para
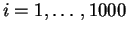
, si
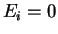
entonces
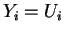
, si no,
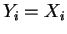
. Repetir los cálculos que siguen para
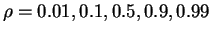
.
- Calcular la tabla de contingencia del par
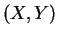 .
.
- Calcular la tabla de los perfiles-linea y de los
perfiles-columnas.
- Calcular la distancia de chi-cuadrado de
contingencia del par
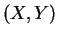 y hacer un test de la independencia
de las dos distribuciones, con umbral
y hacer un test de la independencia
de las dos distribuciones, con umbral
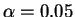 .
.
Ejercicio 18
- Para
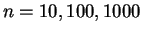 y
y
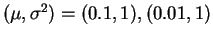 , simular una muestra de tamaño
, simular una muestra de tamaño 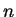 de la ley
de la ley
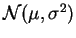 , y hacer un test de la hipótesis
, y hacer un test de la hipótesis
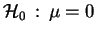 con umbral
con umbral
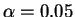 , suponiendo
primero que
, suponiendo
primero que 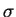 es conocida y después suponiendo que es
desconocida.
es conocida y después suponiendo que es
desconocida.
- Para
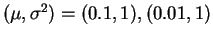 :
:
- Suponiendo
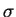 conocida, determinar el tamaño
conocida, determinar el tamaño 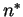 de
la muestra a partir del cual la probabilidad de rechazo de
de
la muestra a partir del cual la probabilidad de rechazo de
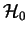 es mayor o igual que
es mayor o igual que 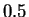 .
.
- Simular
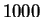 muestras de tamaño
muestras de tamaño 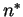 de la ley
de la ley
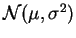 , hacer
para cada una un test de la hipótesis
, hacer
para cada una un test de la hipótesis
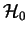 de
umbral
de
umbral
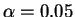 y contar el número de rechazos.
y contar el número de rechazos.
- Para
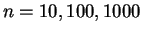 y
y
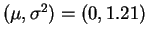 y
después
y
después 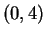 , simular una muestra de tamaño
, simular una muestra de tamaño 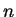 de la ley
de la ley
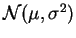 , y hacer un test de la hipótesis
, y hacer un test de la hipótesis
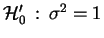 , con umbral
, con umbral
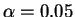 .
.
- Para
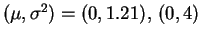 :
:
- Determinar el tamaño
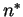 de la muestra a partir del cual
la probabilidad de rechazo de
de la muestra a partir del cual
la probabilidad de rechazo de
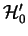 es mayor o igual que
es mayor o igual que
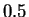 .
.
- Simular 1000 muestras de tamaño
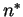 de la ley
de la ley
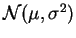 , hacer un test para cada una de ellas de
la hipótesis
, hacer un test para cada una de ellas de
la hipótesis
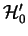 con umbral
con umbral
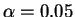 y contar el
número de rechazos.
y contar el
número de rechazos.
Ejercicio 20
- Para
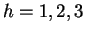 , simular una muestra
, simular una muestra 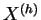 de tamaño
de tamaño
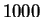 de la ley normal
de la ley normal
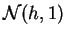 . Calcular las
. Calcular las 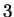 medias y
las
medias y
las 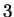 varianzas empíricas.
varianzas empíricas.
- Calcular las varianzas
inter-clases e intra-clases así como la varianza de la muestra
global.
- Calcular el valor que toma el estadígrafo del test
ANOVA y el p-valor correspondiente.
- Retomar los mismos
cálculos con
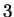 muestras de tamaño
muestras de tamaño 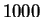 de las leyes
de las leyes
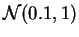 ,
,
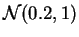 y
y
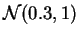 .
.
- Retomar
los mismos cálculos con
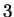 muestras de tamaño
muestras de tamaño 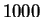 de las leyes
de las leyes
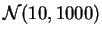 ,
,
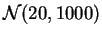 y
y
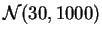 .
.
Sección : Tests Estadísticos
Previo : Función potencia
Siguiente : Índice

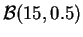 ,
,
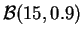 ,
,
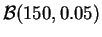 .
. 
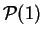 ,
,
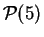 .
. 
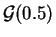 ,
,
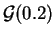 .
.
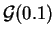 .
.

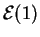 ,
,
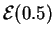 ,
,
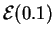 .
. 
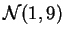 ,
,
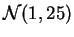 ,
,
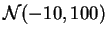 .
. 
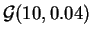 ,
,
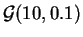 ,
,
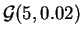 .
.

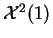 ,
,
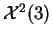 .
. 
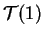 ,
,
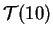 .
. 
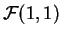 ,
,
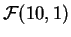 ,
,
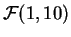 .
.
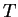 toma el valor
toma el valor 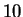 . ¿Que decisión toma usted con
umbral
. ¿Que decisión toma usted con
umbral
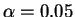 para un test unilateral a la derecha, si la
ley de
para un test unilateral a la derecha, si la
ley de 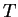 bajo
bajo
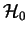 es
es 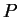 ?.
?.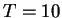 .
.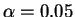 .
.
![$\displaystyle T_u = \sum_{i=1}^n \mathbb {I}_{(-\infty,u]}(X_i)\;,
$](img597.gif)