En numerosas situaciones, se busca
explicar las diferencias observadas en un carácter
estadístico, atribuyendo estas diferencias a otros carácteres
observados en los mismos individuos. En el
análisis de varianza,
los carácteres explicativos (factores) sólo podían tomar un
número finito de modalidades. Los modelos de
regresión
están, sobre todo, adaptados al caso en que los carácteres
explicativos son continuos.
La modelación probabilista considera que la medición (a
explicar) en un individuo dado es una variable aleatoria, cuya ley
depende de los valores que toman en ese individuo los carácteres
explicativos, considerados como deterministas. Si ![]() denota la
variable aleatoria asociada al individuo
denota la
variable aleatoria asociada al individuo ![]() , y
, y
![]() los valores que toman para ese
individuo los carácteres explicativos
los valores que toman para ese
individuo los carácteres explicativos
![]() ,
se separará el efecto determinista y el efecto aleatorio con un
modelo del tipo:
,
se separará el efecto determinista y el efecto aleatorio con un
modelo del tipo:
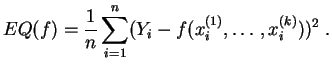
En algunos casos clásicos, se sabe resolver explícitamente este problema de minimización, y la solución está implementada en los sistemas de cálculo estadístico. Cuando una solución explícita es imposible, se recurre a algoritmos de minimización, uno de ellos es el algoritmo del gradiente.
Nosotros consideraremos solamente la regresión lineal simple :
Los valores de ![]() y
y ![]() que minimizan el error cuadrático se
expresan en función de las
medias,
varianzas y
covarianzas
empíricas de
que minimizan el error cuadrático se
expresan en función de las
medias,
varianzas y
covarianzas
empíricas de ![]() y de
y de ![]() . Denotamos:
. Denotamos:
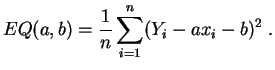
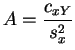 y
yEl error cuadrático minimal es:
Estas tres variables aleatorias son
estimadores
convergentes de
![]() ,
, ![]() y
y ![]() respectivamente. Se obtiene un estimador
sin
sesgo y convergente de
respectivamente. Se obtiene un estimador
sin
sesgo y convergente de ![]() tomando:
tomando:
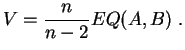
El siguiente resultado permite calcular las leyes de estos estimadores, y por tanto deducir tests sobre los valores de los parámetros. Se le puede considerar como una extensión del teorema 3.1.
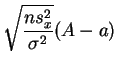 sigue
la
ley normal
sigue
la
ley normal
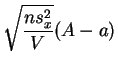 sigue la
ley de
Student
sigue la
ley de
Student
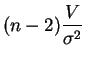 sigue la
ley de
chi-cuadrado
sigue la
ley de
chi-cuadrado
La primera hipótesis que queremos comprobar es que el
carácter explicativo no aporta información, es decir que la
pendiente ![]() de la
recta de
regresión lineal es nula:
de la
recta de
regresión lineal es nula:
Según que ![]() se suponga conocido o desconocido, se
utilizará el inciso 1 o el inciso 2 del teorema.
Supongamos por ejemplo que
se suponga conocido o desconocido, se
utilizará el inciso 1 o el inciso 2 del teorema.
Supongamos por ejemplo que ![]() sea desconocido, el
estadígrafo de test es:
sea desconocido, el
estadígrafo de test es:
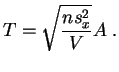
Para el test
bilateral de umbral ![]() , la regla de decisión
es:
, la regla de decisión
es:
Este test está evidentemente muy cercano del
test de
correlación, aún si las hipótesis de modelación son
diferentes.