
Pour décomposer cette image, on utilise donc deux filtres issus du choix d'ondelette : un filtre passe-haut et un filtre passe-bas.
Seules deux types de transformations s'appuyant sur deux types d'ondelettes ont été choisis pour le format JPEG2000 :
NB : pour la CDF 9 7 :

Ces figures représentent les ondelettes discrétisées:
![\includegraphics[width=9.5cm]{ondelette97.eps}](img80.png)
![\includegraphics[width=9.5cm]{ondeletteSpline.eps}](img81.png)
|
A partir de ces ondelettes, nous formons donc les deux filtres : nous noterons H le filtre passe-haut, et L le filtre passe-bas. Cette phase s'appelle la phase d'analyse.
La ligne du haut correspond aux images convoluées avec le filtre L. La ligne du bas correspond aux images convoluées avec le filtre H.
L'itération suivante se fera en prenant pour image de base, la partie LL, correspondant à la convolution par le filtre passe-bas (horizontalement, et verticalement). Le format JPEG2000 limite le nombre d'itérations D entre 0 et 32, les valeurs par défaut étant la plupart du temps entre 4 et 8. Si on regarde plus généralement l'effet de cette transformation, il apparait que cet algorithme concentre l'énergie de l'image dans les blocs LL de plus haut niveau de décomposition. Ensuite tous les autres blocs ne sont que des détails de l'image. Ainsi des manières de compresser et donc de mettre à zéro une partie des coefficients de cette matrice reviennent à analyser les blocs de plus haut niveau de décomposition, et de faire une supposition : les valeurs faibles dans les hauts degrés de décomposition tendent vers zéro au fur et à mesure que l'on remonte les niveaux.
Cette méthode permettra de compresser énormément les zones relativement continues, mais en gardant l'ensemble des discontinuités, et cela en suivant le contour de l'image, puisque les filtres passe-haut sont appliqués dans toutes les directions : verticale, horizontale et diagonale (composition des deux).
Pour schématiser autrement :
Pour reconstituer ensuite l'image, nous procédons à la phase dite de synthèse. Pour cela on construit les filtres ![]() et
et ![]() .
.
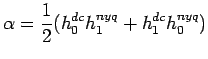
![]() correspond au gain du filtre pour la phase d'analyse à la fréquence DC.
correspond au gain du filtre pour la phase d'analyse à la fréquence DC.
![]() correspond au gain du filtre pour la phase d'analyse à la fréquence de Nyquist.
correspond au gain du filtre pour la phase d'analyse à la fréquence de Nyquist.
![$\displaystyle h_b^{dc} = {\displaystyle \sum_{n}h_b[n]}
$](img94.png)
![$\displaystyle h_b^{nyq} = {\displaystyle \sum_n(-1)^nh_b[n]}
$](img95.png)
pour b=0,1