The software has been tested for some configuration of particles network
- 1 particles Source code
- 2 particles two particles
- 20 particles on a line code structure and installation
- 25 particles on a grid of size 5x5x1 with no exchange a grid of 5x5 particles with no Heissenberg exchange
- 25 particles on a grid of size 5x5x1 with exchange a grid of 5x5 particles with Heissenberg exchange
Source code
We applied an external H_{ext}=(1,0,0) to a magnetic particle with magnetic moment \mu=(0,1,0) and we study the evolution of \mu and E depending on the stochastic noise.
Deterministic case
The deterministic case test is computed by the ito problem without any noise. The evolution of the deterministic trajectory is as follow
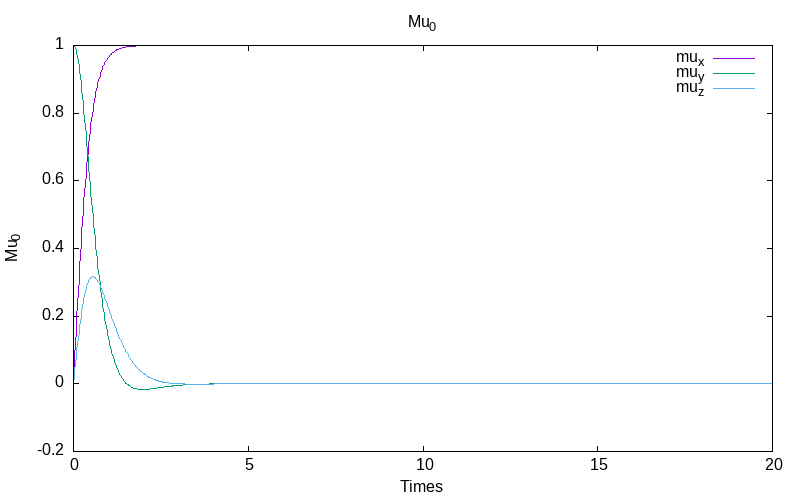 |
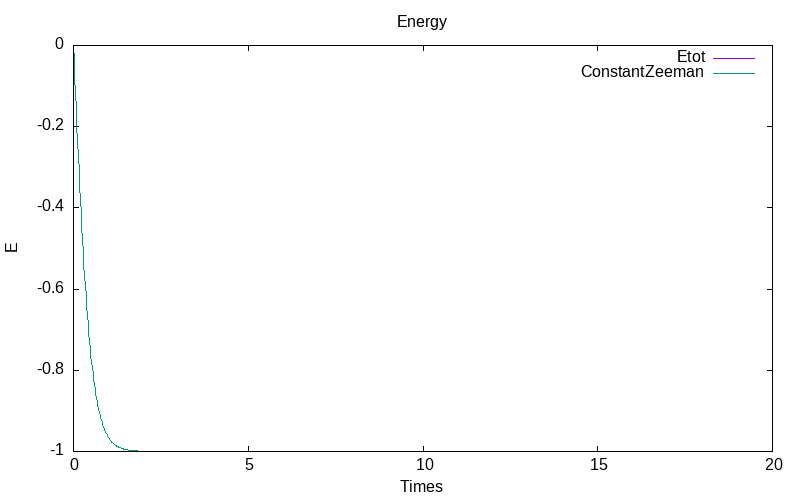 |
| evolution of mu | the energy evolution |
Ito system with constant noise rate
For the Ito stochastic model with constant noise \epsilon=0.1, we obtain for the first simulation:
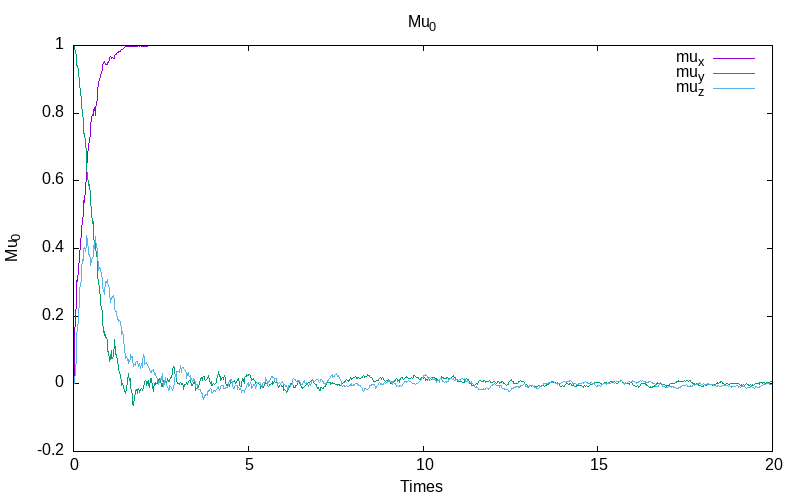 |
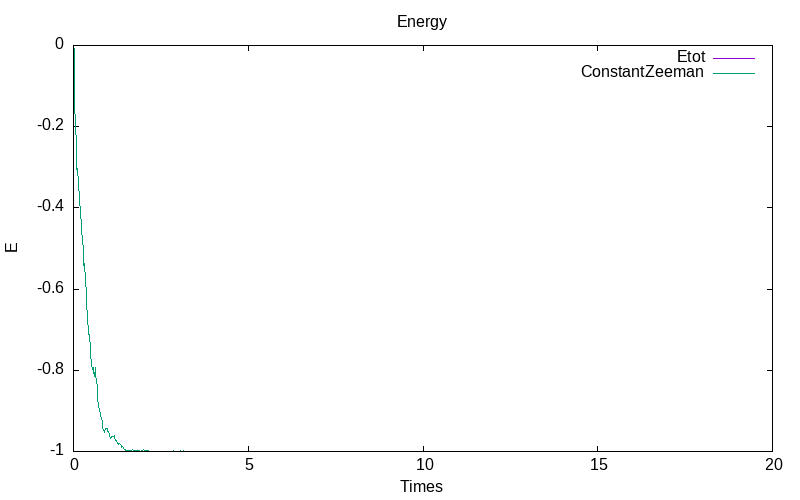 |
| evolution of mu | the energy evolution |
The mean of the total energies for the determinitic and stochastic models gives :
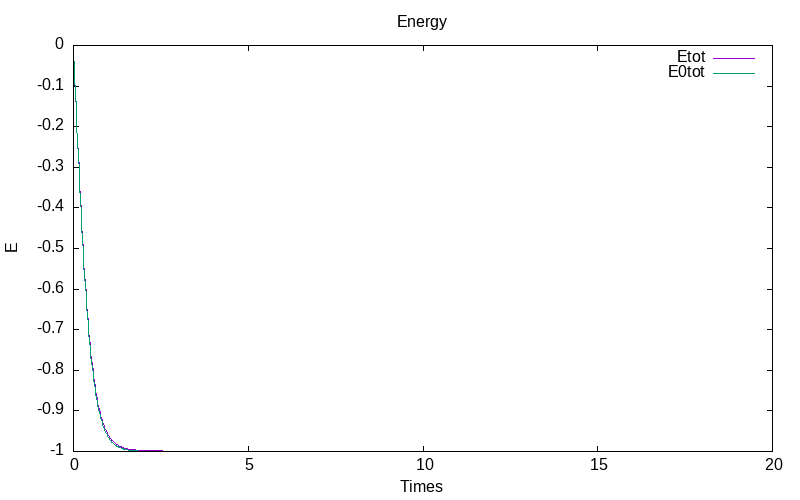 |
| evolution of means of E |
Ito system with inverse noise rate
For the Ito stochastic model with inverse noise \epsilon=\frac{0.1}{1+t}, we obtain for the first simulation:
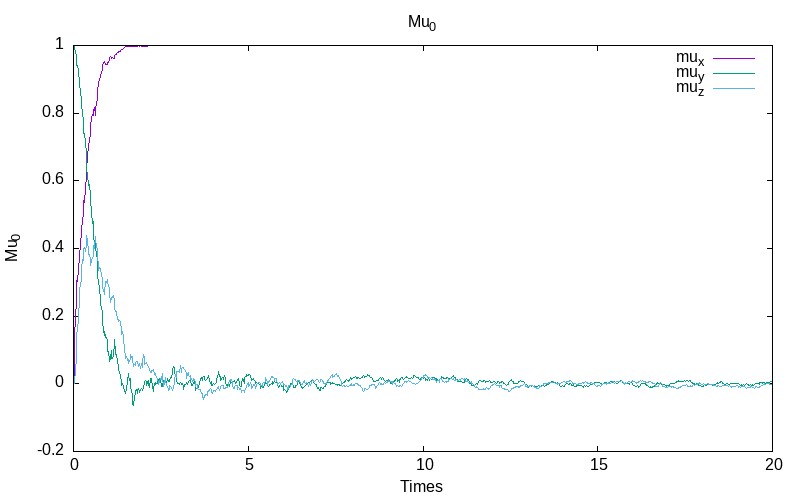 |
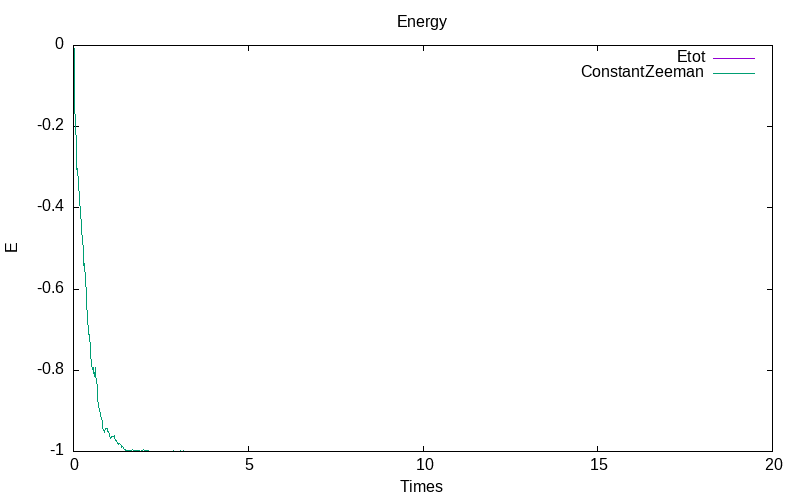 |
| evolution of mu | the energy evolution |
The mean of the total energies for the determinitic and stochastic models gives :
 |
| evolution of means of E |
Stratonovich system with inverse noise rate
For the Stratanovich stochastic model, the magnetic moment \mu is not normalized in the algorithm but the norm of \mu in the Landau Lifschitz equation is explicitly set to 1.
For the this model with inverse noise \epsilon=\frac{0.1}{1+t}, we obtain for the first simulation:
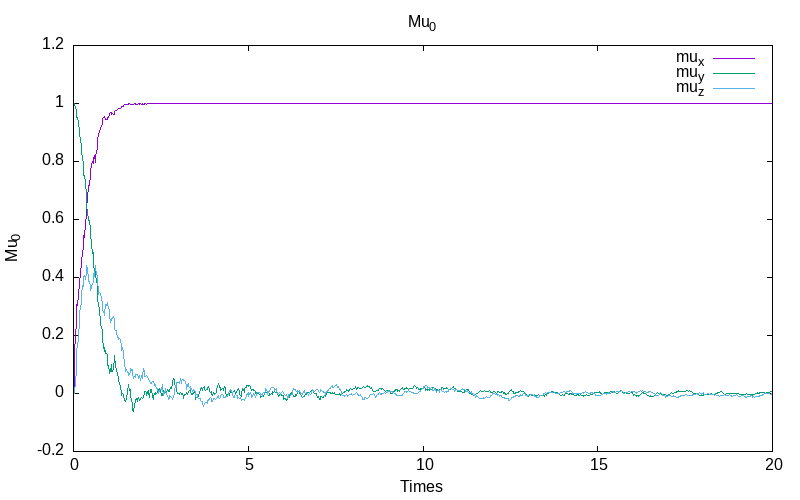 |
 |
| evolution of mu | the energy evolution |
The mean of the total energies for the determinitic and stochastic models gives :
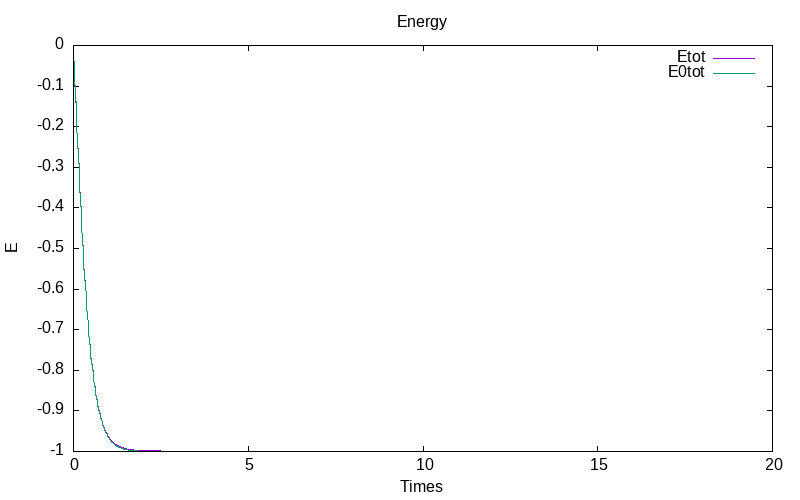 |
| evolution of means of E |
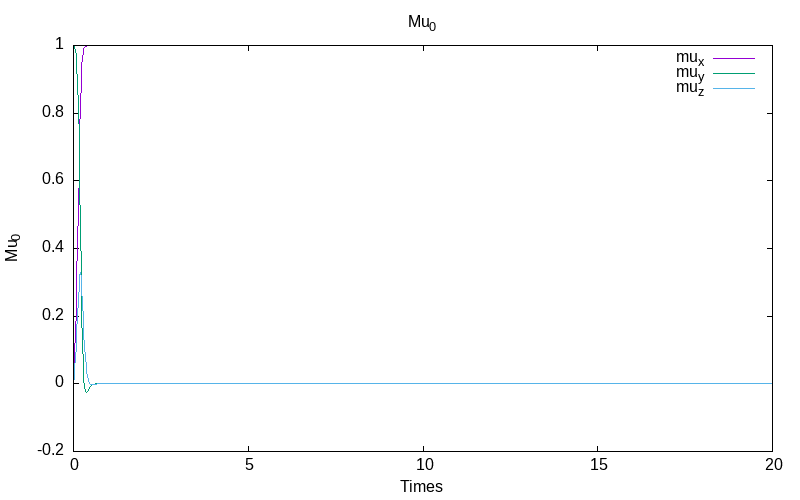
Normalized Stratonovich system with inverse noise rate
For the this model with inverse noise \epsilon=\frac{0.1}{1+t}, we obtain for the first simulation:
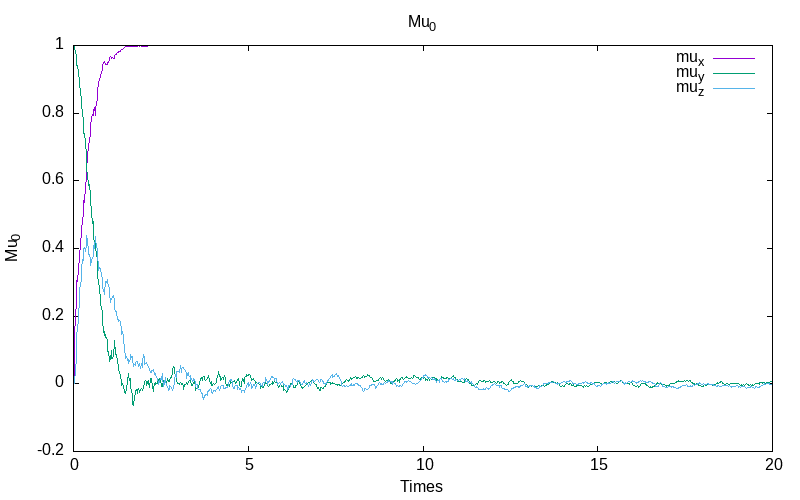 |
 |
| evolution of mu | the energy evolution |
The mean of the total energies for the determinitic and stochastic models gives :
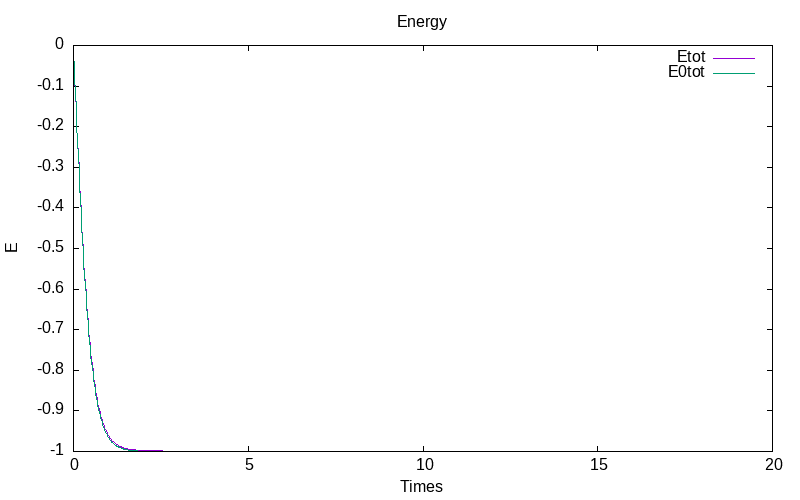 |
| evolution of means of E |
two particles
We applied an external H_{ext}=(1,0,0) to two magnetic particles with initial magnetic moment \mu=(0,1,0). The distance between the 2 particles is 1 wheras the exchange coefficient is 1 ( J_{01}=J_{10}=1 and J_{00}=J_{11}=-1).
We study the evolution of \mu and E depending on the stochastic noise.
Deterministic case
The deterministic case test is computed by the ito problem without any noise. The evolution of the deterministic trajectory is as follow
 |
 |
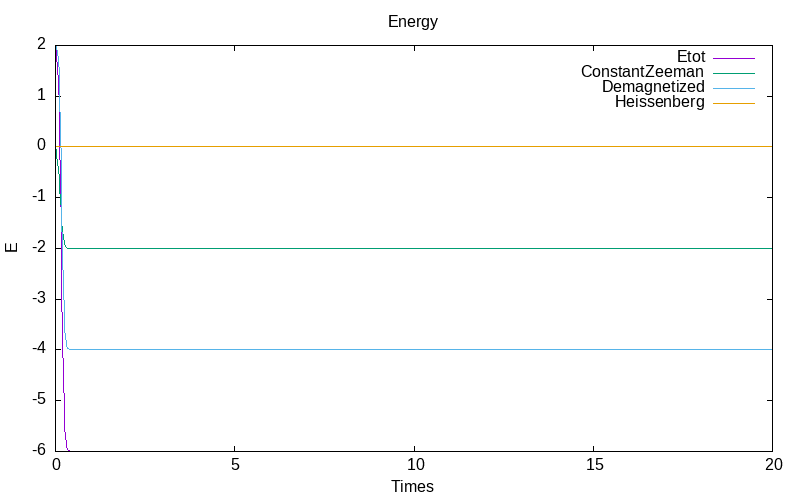 |
| evolution of mu for particle 0 | evolution of mu for the particle 1 /td> | evolution of the energies |
Ito system with constant noise rate
For the Ito stochastic model with constant noise \epsilon=0.1, we obtain for the first simulation:
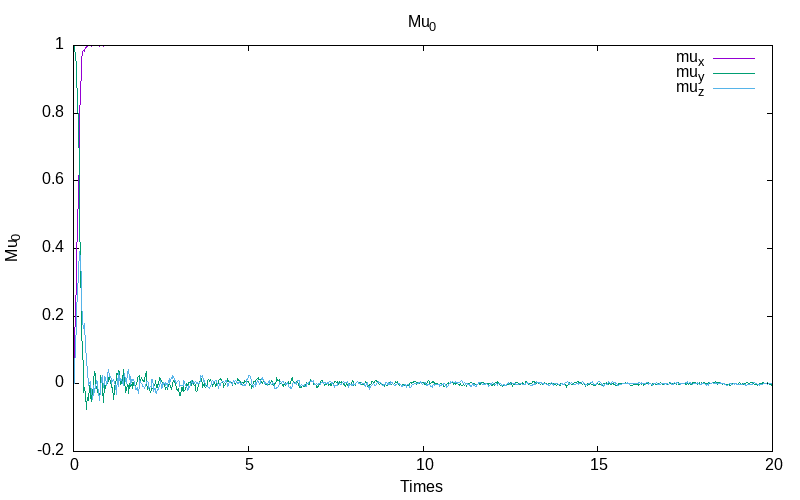 |
 |
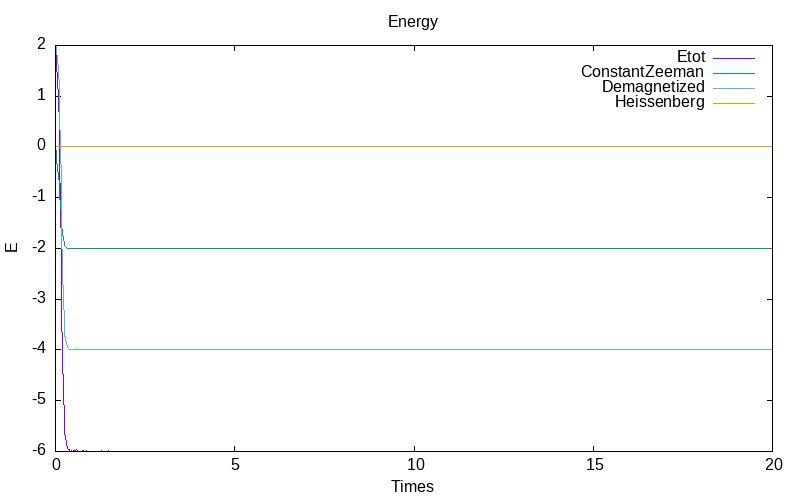 |
| evolution of mu for particle 0 | evolution of mu for the particle 1 /td> | evolution of the energies |
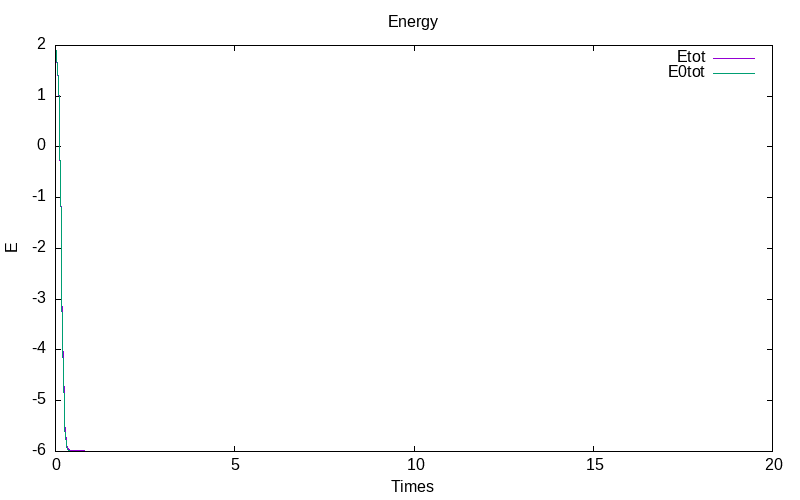 |
| evolution of means of E |
Ito system with inverse noise rate
For the Ito stochastic model with inverse noise \epsilon=\frac{0.1}{1+t}, we obtain for the first simulation:
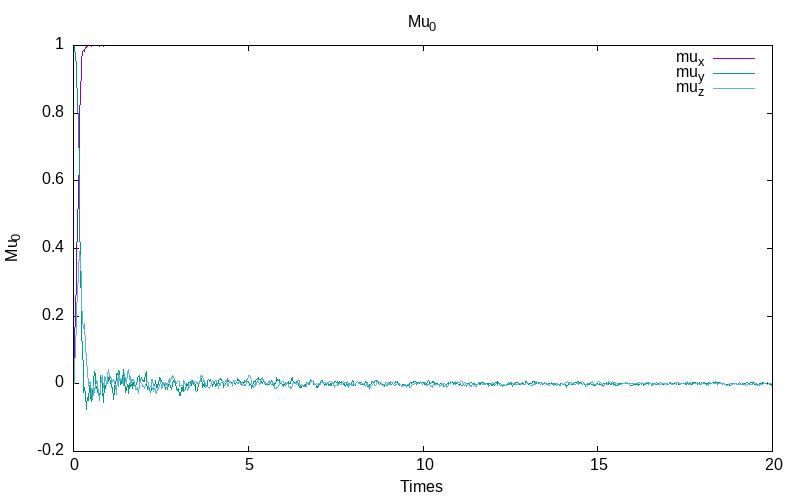 |
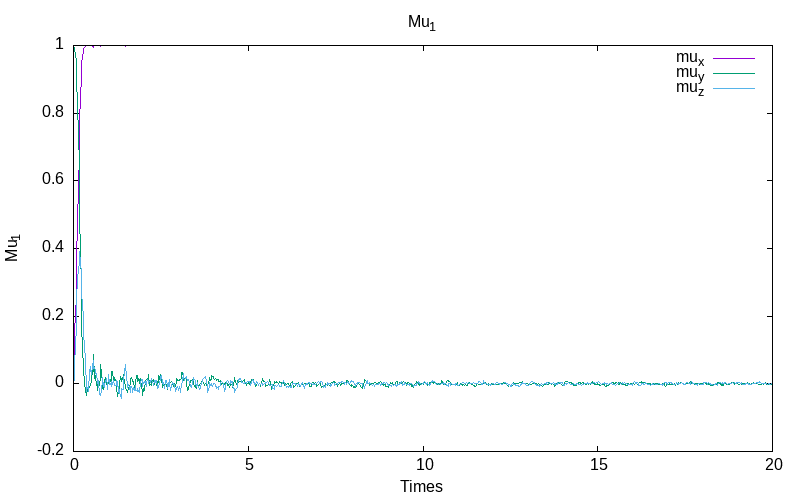 |
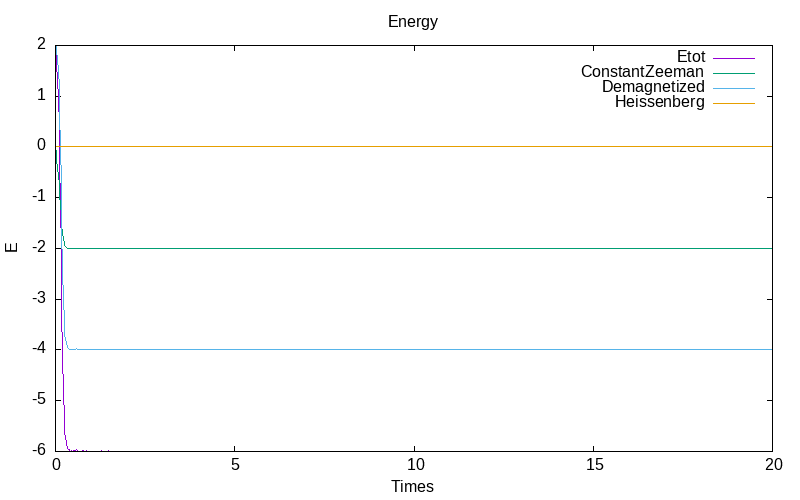 |
| evolution of mu for particle 0 | evolution of mu for the particle 1 /td> | evolution of the energies |
 |
| evolution of means of E |
Stratonovich system with inverse noise rate
For the Stratonovich stochastic model with inverse noise \epsilon=\frac{0.1}{1+t}, we obtain for the first simulation:
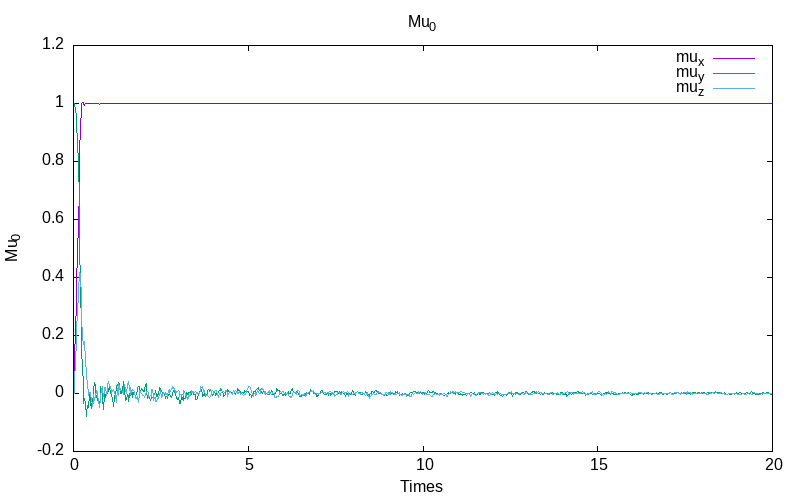 |
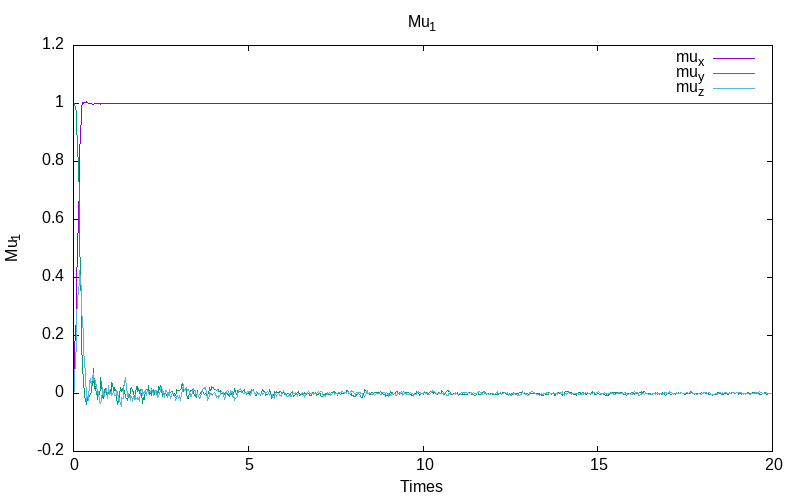 |
 |
| evolution of mu for particle 0 | evolution of mu for the particle 1 /td> | evolution of the energies |
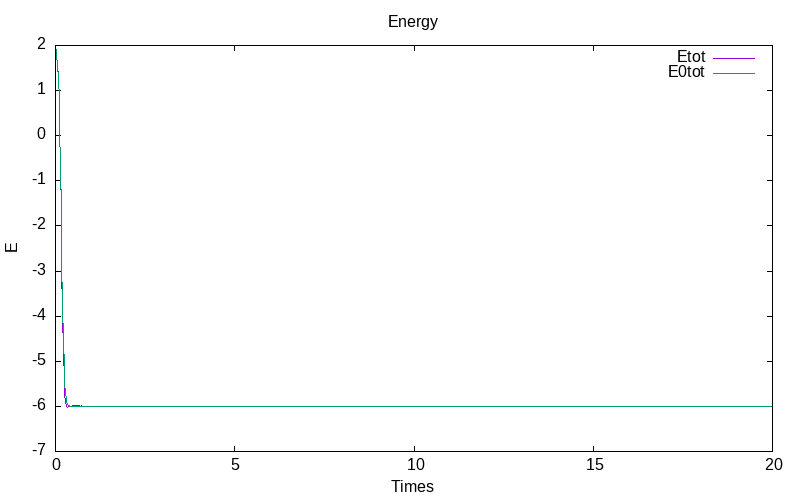 |
| evolution of means of E |
Normalized Stratonovich system with inverse noise rate
For the Normalized Stratonovich stochastic model with inverse noise \epsilon=\frac{0.1}{1+t}, we obtain for the first simulation:
 |
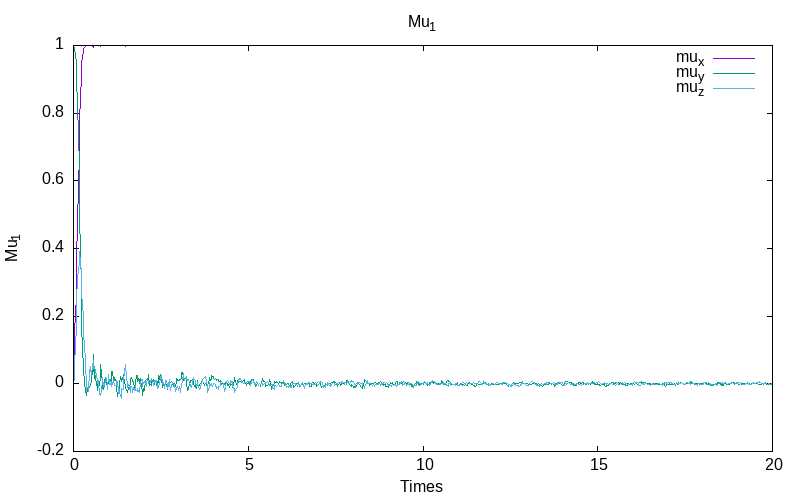 |
 |
| evolution of mu for particle 0 | evolution of mu for the particle 1 /td> | evolution of the energies |
 |
| evolution of means of E |
code structure and installation
We applied an external H_{ext}=(1,0,0) to 20 magnetic particles located on a line with initial random magnetic moment. The distance between the 2 particles is 1 wheras the exchange coefficient is 1 ( J_{i,i+1}=J_{i+1,i}=1 and J_{0,0}=J_{19,19}=-1 and \forall i in {1,18}, J_{i,i}=-2).
We study the evolution of \mu and E depending on the stochastic noise.
Deterministic case
The deterministic case test is computed by the ito problem without any noise. The evolution of the deterministic trajectory is as follow
 |
 |
 |
| evolution of mu for all particles | evolution of mu for the particle 17 /td> | evolution of the energies |
Normalized Stratonovich with inverse noise rate
Note that the Stratonovich model diverges for the coputing of mu. So we chose to show only the Normalized Stratonovich system with inverse noise \varepsilon=\frac{0.1}{1+t} ,
 |
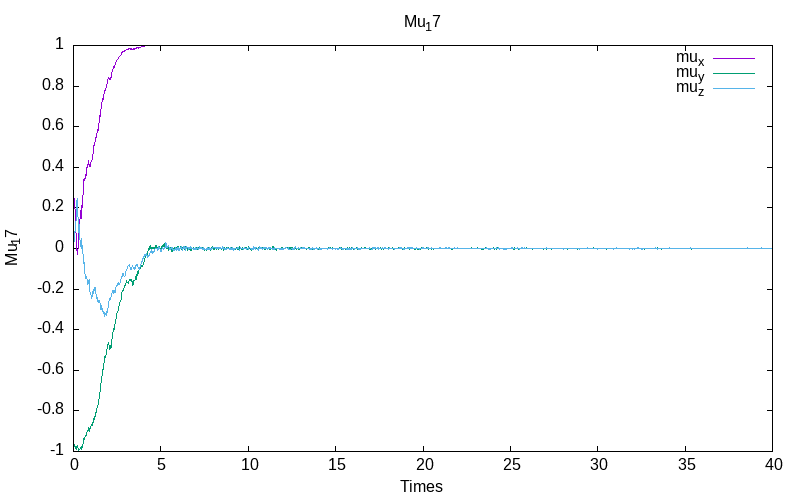 |
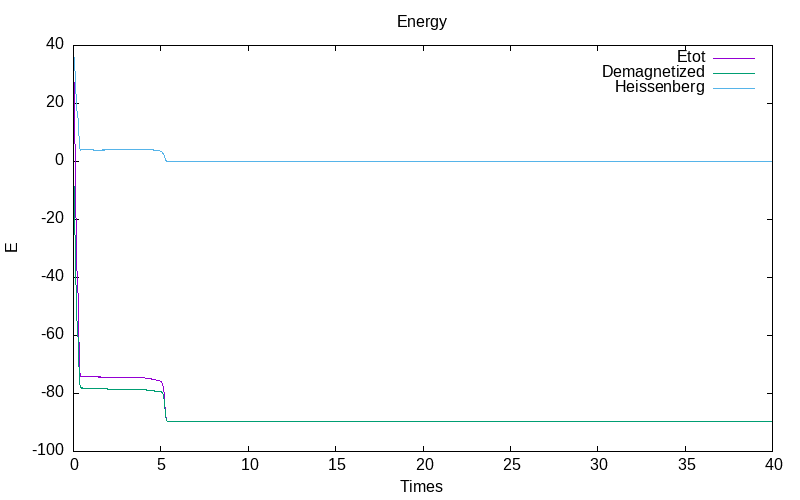 |
| evolution of mu for all particles | evolution of mu for the particle 17 /td> | evolution of the energies |
a grid of 5x5 particles with no Heissenberg exchange
We applied no external magnetic field to 5x5x1 magnetic particles located on a grid with initial magnetic moment \mu=(0,1,0) or \mu=(0,-1,0) in half of the domain. The step size of the grid is 1 in all directions. The Heissenberg operator is neglected.
We study the evolution of \mu and E depending on the stochastic noise.
Deterministic case
The deterministic case test is computed by the ito problem without any noise. The evolution of the deterministic trajectory is as follow
 |
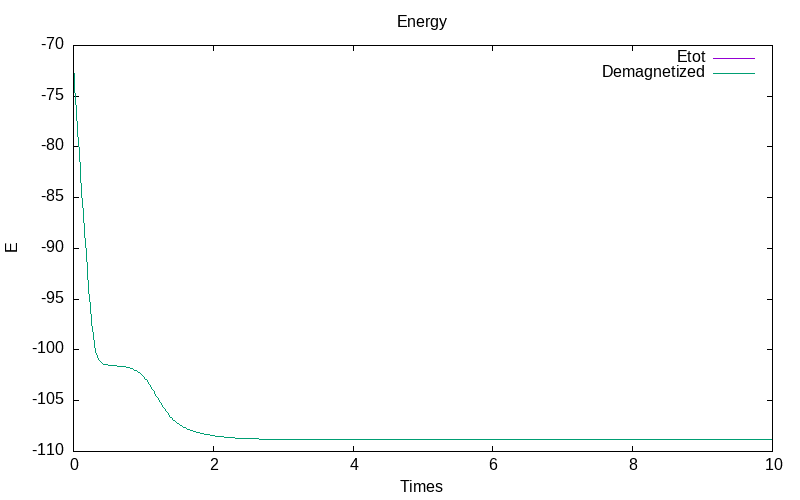 |
| evolution of mu for all particles | evolution of the energies |
Normalized Stratonovich with inverse noise rate
Note that the Stratonovich model diverges for the coputing of mu. So we chose to show only the Normalized Stratonovich system with inverse noise \varepsilon=\frac{0.1}{1+t} ,
 |
 |
| evolution of mu for all particles | evolution of the energies |
a grid of 5x5 particles with Heissenberg exchange
We applied no external magnetic field to 5x5x1 magnetic particles located on a grid with initial magnetic moment \mu=(0,1,0) or \mu=(0,-1,0) in half of the domain. The step size of the grid is 1 in all directions and each particle is linked to all particles where its distance is less than 1 in each direction. he Heissenberg coefficient between 2 linked particles i and j verifies J_{ij}=1 \forall i \neq j and J_{ii}=-\sum_{j \neq i} J_{ij}.
We study the evolution of \mu and E depending on the stochastic noise.
Deterministic case
The deterministic case test is computed by the ito problem without any noise. The evolution of the deterministic trajectory is as follow
 |
 |
| evolution of mu for all particles | evolution of the energies |
Normalized Stratonovich with inverse noise rate
Note that the Stratonovich model diverges for the coputing of mu. So we chose to show only the Normalized Stratonovich system with inverse noise \varepsilon=\frac{0.1}{1+t} ,
 |
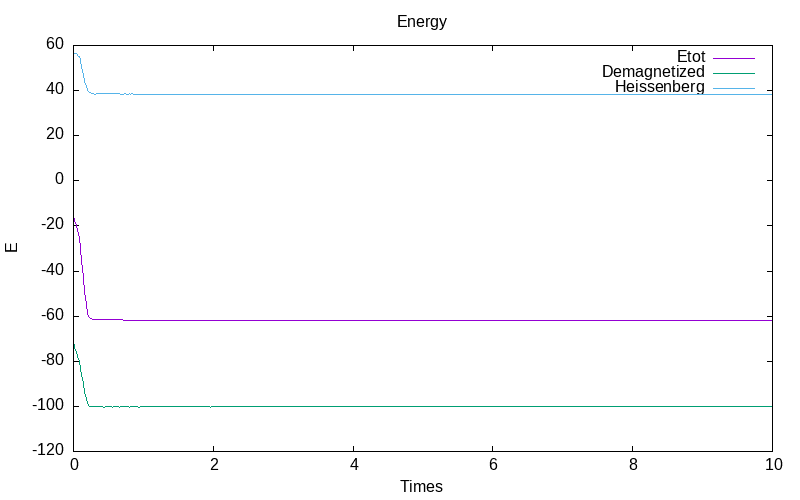 |
| evolution of mu for all particles | evolution of the energies |