dpackedsymmatrix_functions.h File Reference

#include "lapack_functions.h"

Include dependency graph for dpackedsymmatrix_functions.h:

This graph shows which files directly or indirectly include this file:

Go to the source code of this file.

Functions
void	DoublePackedSymmetricMatrixVectorProduct (const tLVectorIndex &nX, const tLVectorIncrement &incX, const double *x, const tLVectorIndex &nRows, const double *A, const lapack_real &alpha, const lapack_real &beta, const tLVectorIndex &nY, const tLVectorIncrement &incY, double *y)
	compute Y!=Beta.Y+alpha A.X More...
void	DoublePackedSymmetricMatrixRankSymmetricProduct (const tLVectorIncrement &incX, const double *X, const double &alpha, const tLVectorIndex &nSRows, double *S)
	compute the symmetric matrix S+=alpha X tX More...
void	DoublePackedSymmetricMatrixMatrixProduct (const tBoolean &isLeftSide, const tLVectorIndex &nRowsS, const double *S, const tLVectorIndex &nRowsB, const tLVectorIndex &nColsB, const tLVectorIncrement &incB, const tLVectorIndex &ldB, const tBoolean &isBSymmetric, const tBoolean &isBFull, const double *B, const lapack_real &alpha, const lapack_real &beta, const tLVectorIndex &nRowsC, const tLVectorIndex &nColsC, const tLVectorIncrement &incC, const tLVectorIndex &ldC, double *C)
	compute : More...
void	DoublePackedSymmetricMatrixKRankSymmetricProduct (const tLVectorIndex &nRowsA, const tLVectorIndex &nColsA, const tLVectorIncrement &incA, const tLVectorIndex &ldA, const tBoolean &isTransA, const double *A, const double &alpha, const double &beta, const tLVectorIndex &nD, const tLVectorIncrement &incD, const double *D, const tLVectorIndex &nS, double *S)
	compute : S:=beta S+ alpha op(A) . D . top(A) If D is null D is supposed to be identity (fortran version) If not, (extended C version) More...
tBoolean	DoublePackedSymmetricMatrixEigenValues (const tLVectorIndex &nRowsA, double *A, const tLVectorIndex &nU, double *U, const tLVectorIndex &ldW, double *W)
	compute all the eigen values or vectors (if W is not null or ldW<=1) More...
tBoolean	DoublePackedSymmetricMatrixBoundedEigenValues (const tLVectorIndex &nRowsA, double *A, const tLVectorIndex &nU, double *U, const tLVectorIndex &minIndex, const tLVectorIndex &maxIndex, const double &minBound, const double &maxBound, const tLVectorIndex &ldW, double *W)
	compute the selected eigen values or vectors (if W is not null or ldW<=1) with More...
tBoolean	DoublePackedSymmetricMatrixCholeskyFactorization (const tLVectorIndex &nRowsA, double *A)
	make the cholesky factorization A=tU.U More...
tBoolean	DoublePackedSymmetricMatrixBunchKaufmanFactorization (const tLVectorIndex &nRows, double *A, lapack_int *ipiv)
	make the Bunch Kaufman factorization A=U.D.tU More...
tBoolean	DoublePackedSymmetricMatrixInverse (const tLVectorIndex &nRows, const lapack_int *ipiv, double *A)
	inverse the pack symmetric matrix where is has ben Bunch Kaufman factorized More...

Function Documentation

tBoolean DoublePackedSymmetricMatrixBoundedEigenValues	(	const tLVectorIndex &	nRowsA,
		double *	A,
		const tLVectorIndex &	nU,
		double *	U,
		const tLVectorIndex &	minIndex,
		const tLVectorIndex &	maxIndex,
		const double &	minBound,
		const double &	maxBound,
		const tLVectorIndex &	ldW,
		double *	W
	)

compute the selected eigen values or vectors (if W is not null or ldW<=1) with

• index in [minIndex,maxIndex] if in [1,nRows]
• values in [minBound,maxBound] if minBound!=maxBound

compute also the eigen vector if W is not null and ldW >1

References dspevx(), F77NAME, getSafeMinimum(), lapack_char, lapack_int, lapack_real, null, CORE_String::toString(), and tString.

Referenced by LAP_DoublePackedSymmetricMatrix::computeEigenValueDecomposition().

Here is the call graph for this function:

Here is the caller graph for this function:

tBoolean DoublePackedSymmetricMatrixBunchKaufmanFactorization	(	const tLVectorIndex &	nRows,
		double *	A,
		lapack_int *	ipiv
	)

make the Bunch Kaufman factorization A=U.D.tU

References dsptrf(), F77NAME, lapack_char, and lapack_int.

Referenced by LAP_DoublePackedSymmetricMatrix::inverse().

Here is the call graph for this function:

Here is the caller graph for this function:

tBoolean DoublePackedSymmetricMatrixCholeskyFactorization	(	const tLVectorIndex &	nRowsA,
		double *	A
	)

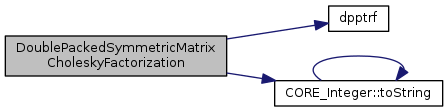
make the cholesky factorization A=tU.U

References dpptrf(), F77NAME, lapack_char, lapack_int, and CORE_Integer::toString().

Here is the call graph for this function:

tBoolean DoublePackedSymmetricMatrixEigenValues	(	const tLVectorIndex &	nRowsA,
		double *	A,
		const tLVectorIndex &	nU,
		double *	U,
		const tLVectorIndex &	ldW,
		double *	W
	)

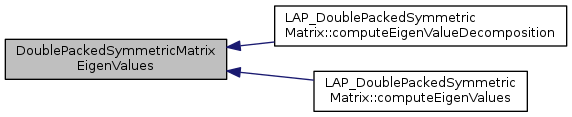
compute all the eigen values or vectors (if W is not null or ldW<=1)

References dspev(), F77NAME, lapack_char, lapack_int, lapack_real, null, CORE_String::toString(), and tString.

Referenced by LAP_DoublePackedSymmetricMatrix::computeEigenValueDecomposition(), and LAP_DoublePackedSymmetricMatrix::computeEigenValues().

Here is the call graph for this function:

Here is the caller graph for this function:

tBoolean DoublePackedSymmetricMatrixInverse	(	const tLVectorIndex &	nRows,
		const lapack_int *	ipiv,
		double *	A
	)

inverse the pack symmetric matrix where is has ben Bunch Kaufman factorized

References dsptri(), F77NAME, lapack_char, lapack_int, and lapack_real.

Referenced by LAP_DoublePackedSymmetricMatrix::inverse().

Here is the call graph for this function:

Here is the caller graph for this function:

void DoublePackedSymmetricMatrixKRankSymmetricProduct	(	const tLVectorIndex &	nRowsA,
		const tLVectorIndex &	nColsA,
		const tLVectorIncrement &	incA,
		const tLVectorIndex &	ldA,
		const tBoolean &	isTransA,
		const double *	A,
		const double &	alpha,
		const double &	beta,
		const tLVectorIndex &	nD,
		const tLVectorIncrement &	incD,
		const double *	D,
		const tLVectorIndex &	nS,
		double *	S
	)

compute : S:=beta S+ alpha op(A) . D . top(A) If D is null D is supposed to be identity (fortran version) If not, (extended C version)

compute : S:=beta S+ alpha op(A) . D . top(A) If D is null D is supposed to be identity (fortran version) If not, (extended C version)

References CNAME, dsprk(), lapack_char, lapack_int, null, and tLVectorIndex.

Referenced by LAP_DoublePackedSymmetricMatrix::rankSymmetricProduct().

Here is the call graph for this function:

Here is the caller graph for this function:

void DoublePackedSymmetricMatrixMatrixProduct	(	const tBoolean &	isLeftSide,
		const tLVectorIndex &	nRowsS,
		const double *	S,
		const tLVectorIndex &	nRowsB,
		const tLVectorIndex &	nColsB,
		const tLVectorIncrement &	incB,
		const tLVectorIndex &	ldB,
		const tBoolean &	isBSymmetric,
		const tBoolean &	isBFull,
		const double *	B,
		const lapack_real &	alpha,
		const lapack_real &	beta,
		const tLVectorIndex &	nRowsC,
		const tLVectorIndex &	nColsC,
		const tLVectorIncrement &	incC,
		const tLVectorIndex &	ldC,
		double *	C
	)

compute :

• C:=beta C+ alpha S. B
• C:=beta C+ alpha B. S where :

S is packed symmetric

• B is general full matrix (extanded C Version)
• B is symmetric full matrix (extanded C Version),
• B is packed symmetric matrix (extended C version)
• C is general full matrix

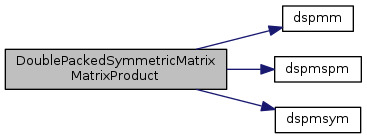
References CNAME, dspmm(), dspmspm(), dspmsym(), lapack_char, and lapack_int.

Referenced by LAP_DoublePackedSymmetricMatrix::matrixProduct().

Here is the call graph for this function:

Here is the caller graph for this function:

void DoublePackedSymmetricMatrixRankSymmetricProduct	(	const tLVectorIncrement &	incX,
		const double *	X,
		const double &	alpha,
		const tLVectorIndex &	nSRows,
		double *	S
	)

compute the symmetric matrix S+=alpha X tX

References dspr(), F77NAME, lapack_char, and lapack_int.

Referenced by LAP_DoublePackedSymmetricMatrix::dotProduct().

Here is the call graph for this function:

Here is the caller graph for this function:

void DoublePackedSymmetricMatrixVectorProduct	(	const tLVectorIndex &	nX,
		const tLVectorIncrement &	incX,
		const double *	x,
		const tLVectorIndex &	nRows,
		const double *	A,
		const lapack_real &	alpha,
		const lapack_real &	beta,
		const tLVectorIndex &	nY,
		const tLVectorIncrement &	incY,
		double *	y
	)

compute Y!=Beta.Y+alpha A.X

References dspmv(), F77NAME, lapack_char, and lapack_int.

Referenced by LAP_DoublePackedSymmetricMatrix::vectorProduct().

Here is the call graph for this function:

Here is the caller graph for this function: