Thèse de doctorat
"Modélisation mathématique et simulation numérique
pour des dispositifs nanoélectroniques innovants".
Cette thèse en cotutelle
(disponible ici au format PDF) a été soutenue le 25 novembre 2011 devant un jury composé de :
| P. Degond |
(CNRS IMT Toulouse) |
directeur de thèse, |
| L. Desvillettes |
(CMLA ENS Cachan) |
rapporteur, |
| A. Jüngel |
(TU Wien) |
rapporteur, |
| I. Perugia |
(DIMAT Pavia) |
examinatrice, |
| P. Pietra |
(IMATI-CNR Pavia) |
directrice de thèse, |
| J.-M. Roquejoffre |
(IMT Toulouse) |
examinateur. |
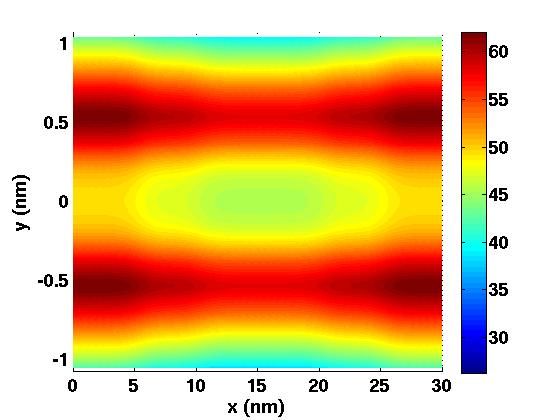
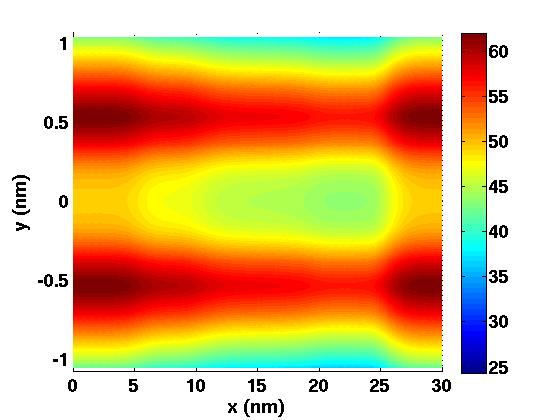
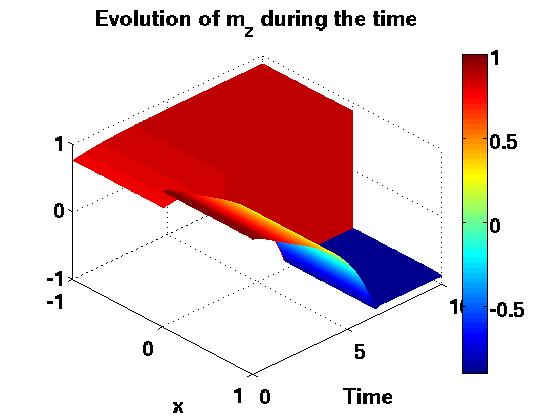
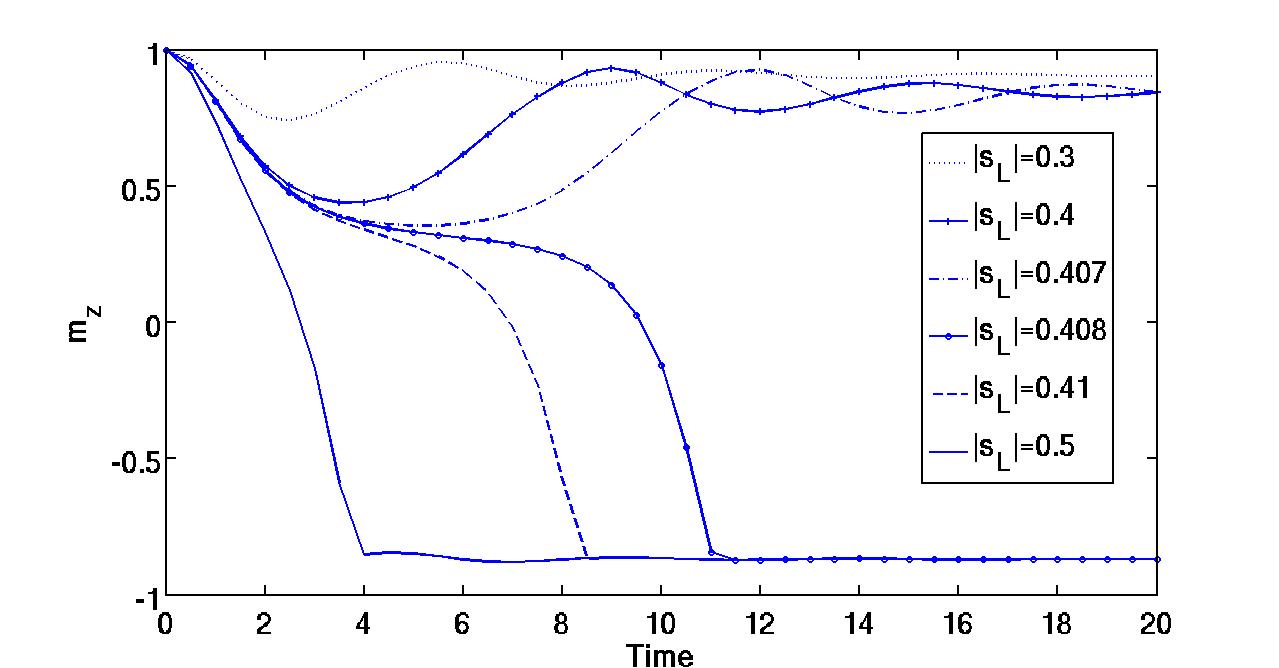
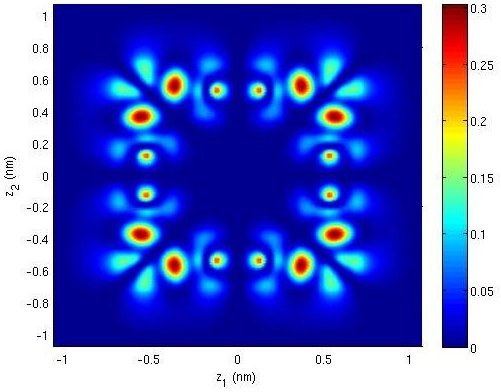
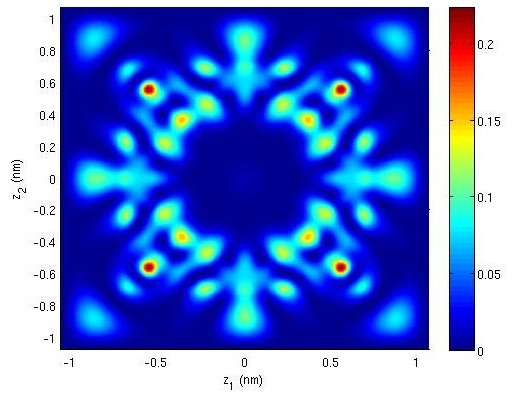
Dans cette thèse, nous nous intéressons à la modélisation et la simulation de dispositifs nanoélectroniques innovants. Premièrement, nous dérivons formellement un modèle avec masse effective pour décrire le transport quantique des électrons dans des nanostructures très fortement confinées. Des simulations numériques illustrent l'intérêt du modèle obtenu pour un dispositif simplifié mais déjà significatif. La deuxième partie est consacrée à l'étude du transport non ballistique dans ces mêmes structures confinées. Nous analysons rigoureusement un modèle de drift-diffusion et puis nous décrivons et implémentons une approche de couplage spatial classique-quantique. Enfin, nous modélisons et simulons un nanodispositif de spintronique. Plus précisement, nous étudions le renversement d'aimantation dans un matériau ferromagnétique multi-couches sous l'effet d'un courant de spin.
Mots-clés : nanostructures à fort confinement, approximation de la masse effective, transport classique/quantique, système Schrödinger-Poisson, équation de dérive-diffusion, spintronique et transfert de spin, équation de Landau-Lifshitz, analyse multi-échelles, développements asymptotiques, calcul haute-performance.