Section : Outils pour l'Algèbre
Avant : Vecteurs et matrices
Après : Réduction des matrices

Systèmes linéaires

Il existe trois moyens différents de résoudre un système linéaire.

$\bullet$

La fonction linsolve résout une liste d'équations linéaires, avec la même syntaxe que solve.

$\bullet$

La fonction simult peut résoudre plusieurs systèmes d'équations linéaires qui ne diffèrent que par leur second membre. Elle prend comme premier argument la matrice du système et comme second argument la matrice dont la (ou les) colonnes sont le (ou les) second membre(s) des systèmes.

$\bullet$

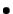
La fonction rref calcule la réduction d'une matrice quelconque sous forme de Gauss-Jordan. Si on borde la matrice du système avec le second membre, rref retourne une matrice contenant le vecteur solution.

Quand le système est impossible, linsolve retourne la liste vide, simult retourne un message d'erreur, rref retourne une matrice dont une des lignes est nulle, sauf le dernier coefficient. Quand le système est indéterminé, linsolve retourne la solution fonction de certaines variables, simult retourne seulement une solution, rref retourne une matrice dont une ou plusieurs lignes sont nulles. L'exemple ci-dessous concerne le système

$$\left\{ \begin{array}{llllllr} x &+& y &+& az&=&1\\ x & +& a y&+& z&=&1 \\ ax & +&y &+& z&=&-2 \end{array}\right.$$

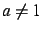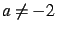Il a une solution unique pour $a\neq 1$ et $a\neq -2$, il est impossible pour 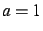$a=1$ et il est indéterminé pour $a=-2$.

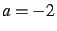linsolve([x+y+a*z=1,x+a*y+z=1,x+a*y+z=-2],[x,y,z])
a:=1
linsolve([x+y+a*z=1,x+a*y+z=1,x+a*y+z=-2],[x,y,z])
a:=-2
linsolve([x+y+a*z=1,x+a*y+z=1,x+a*y+z=-2],[x,y,z])
purge(a)
A:=[[1,1,a],[1,a,1],[a,1,1]]
solve(det(A),a)
A1:=subst(A,a=1)
rank(A1)
image(A1)
ker(A1)
A2:=subst(A,a=-2)
rank(A2)
image(A2)
ker(A2)
b:= [1,1,-2]
B:=tran(b)
simult(A,B)
simult(A1,B)
simult(A2,B)
M:=blockmatrix(1,2,[A,B])
rref(M)
rref(border(A,b))
rref(border(A1,b))
rref(border(A2,b))

Systèmes linéaires
linsolve	résolution d'un système
simult	résolution simultanée de plusieurs systèmes
rref	réduction de Gauss-Jordan
rank	rang
det	déterminant du système

Section : Outils pour l'Algèbre
Avant : Vecteurs et matrices
Après : Réduction des matrices