Section : Statistiques en Scilab
Précédent : Générateurs pseudo-aléatoires.
Suivant : Calculs de moments.

Représentations graphiques.

La fonction plot2d3 permet de représenter des diagrammes en bâtons et a déjà été utilisée. La fonction histplot représente des histogrammes. Son premier paramètre peut être un entier (nombre de classes), auquel cas l'histogramme est régulier, ou un vecteur donnant les bornes des classes.

x=rand(1,1000);
xbasc()
histplot(10,x)
xbasc()
histplot([0,0.2,0.5,0.6,0.9,1],x)
y=grand(x,"exp",1);
xbasc()
histplot(10,y)
xbasc()
histplot(-log([1:-0.1:0.01]),y)

Pour représenter un nuage de points dans le plan, on peut utiliser plot2d avec un style de représentation négatif ou nul. La fonction hist3d représente des histogrammes dans IR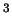$^3$ mais n'effectue pas le calcul des fréquences de classes. Pour cela, on pourra utiliser la fonction freq2d définie ci-dessous. Elle prend en entrée deux vecteurs de bornes, bornex et borney, et une matrice echant, à 2 lignes et 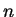$n$ colonnes.

function f = freq2d(echant,bornex,borney) 
//      freq2d retourne une matrice dont les
//      coefficients sont les frequences de echant
//      relatives a bornex et borney

kx = size(bornex,"*")-1;
ky = size(borney,"*")-1;

for i=1:kx,
    for j=1:ky,
        f(i,j) = size(find(..
            echant(1,:) >  bornex(i)   &..
            echant(1,:) <= bornex(i+1) &..
            echant(2,:) >  borney(j)   &..
            echant(2,:) <= borney(j+1)),"*");
   end;
end;
f=f/sum(f);

Cette fonction sera sauvée dans le fichier freq2d.sci. La fonction hist3d prend en entrée une liste formée de la matrice des fréquences, retournée par freq2d, et des deux vecteurs de bornes. Voici quelques exemples d'utilisation.

getf("freq2d.sci")
u=rand(2,2000);
plot2d(u(1,:),u(2,:),0)
bx=[0:0.2:1]; by=bx;
f=freq2d(u,bx,by);
xbasc()
hist3d(list(f,bx,by))

t1=max(rand(2,2000),"r");
t2=min(rand(2,2000),"r");
xbasc()
plot2d(t1,t2,0)
bx=[0:0.2:1]; by=bx;
f=freq2d([t1;t2],bx,by);
xbasc()
hist3d(list(f,bx,by))

M=[0;0]; S=[1,0.8;0.8,1];
v=grand(2000,"mn",M,S);
xbasc()
plot2d(v(1,:),v(2,:),0)
bx=[-3:1.2:3]; by=bx;
f=freq2d(v,bx,by);
xbasc()
hist3d(list(f,bx,by))

On peut visualiser des nuages de points à trois dimensions à l'aide de param3d1, et utiliser la rotation à l'aide de la souris.

M=[0;0;0]; 
S=[1,0.5,0.9 ; 0.5,1,0.3 ; 0.9,0.3,1];
v=grand(10000,"mn",M,S);
xbasc()
param3d1(v(1,:)',v(2,:)',list(v(3,:)',0))

Section : Statistiques en Scilab
Précédent : Générateurs pseudo-aléatoires.
Suivant : Calculs de moments.