Section : Statistiques en Scilab
Précédent : Lois discrètes
Suivant : Représentations graphiques.

Générateurs pseudo-aléatoires.

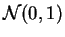Les deux fonctions de génération aléatoire sont rand et grand. Le plus simple est rand. Il retourne des réalisations de variables i.i.d, de loi uniforme sur $[0,1]$ ou de loi normale ${\cal N}(0,1)$, selon l'option.

help rand
// Loi uniforme
unif = rand(1,1000);
histplot(10,unif);
moyennes=cumsum(unif)./[1:1000];
xbasc()
plot(moyennes)
// Loi normale
gauss = rand(1,1000,"normal");
xbasc()
histplot(10,gauss)
// Pile ou face
getf("lois_discretes.sci")
pileface = 2*bool2s(rand(1,1000)<0.5)-1;
[f,v] = freq_emp(pileface)
gains = cumsum(pileface);
plot(gains)
// Loi binomiale
binomiale=sum(rand(4,1000)<0.5,"r");
[f,v] = freq_emp(binomiale)
// Loi exponentielle
expo=-log(unif);
mean(expo)
median(expo)
st_deviation(expo)
xbasc()
histplot(10,expo)
// Loi geometrique
geom = ceil(expo);
[f,v] = freq_emp(geom)
xbasc()
plot2d3("gnn",v',f',5,"111","Geometrique",[0,0,8,max(f)])

Le générateur grand est très complet et nous ne présentons qu'une partie de ses possibilités (voir help grand). Dans les appels de grand pour une loi unidimensionnelle, les deux premiers paramètres m et n spécifient le nombre de lignes et de colonnes de l'échantillon à engendrer. Comme pour rand, ces deux nombres peuvent être remplacés par un vecteur ou une matrice.

getf("lois_discretes.sci")
// Loi binomiale
b=grand(1,1000,"bin",10,0.7);
[f,v]=freq_emp(b)
xbasc()
plot2d3("gnn",v',f',5,"111","Binomiale",[0,0,11,max(f)])
// Loi de Poisson
p=grand(b,"poi",2);
[f,v]=freq_emp(p)
xbasc()
plot2d3("gnn",v',f',5,"111","Poisson",[0,0,8,max(f)])
// Loi du chi-deux
c1=grand(1,1000,"chi",3);
xbasc()
histplot(20,c1)
// Loi gamma
c2=grand(c1,"gam",3/2,1/2);
xbasc()
histplot(20,c2)
// Loi normale dans le plan
M=[0;0]; S=[1,0.8;0.8,1];
X=grand(5000,"mn",M,S);
xbasc()
square(-1,1,-1,1);
plot2d(X(1,:),X(2,:),0);
// Chaine de Markov
P=[0,0.4,0.6;0.2,0.3,0.5;0.5,0.5,0];
X=grand(10000,"markov",P,1);
[f,v]=freq_emp(X)
[x,sta]=linsolve(P'-eye(P),zeros(3,1));
sta=sta/sum(sta,"r")       // mesure stationnaire
abs(f'-sta)

Simulations
grand(m,n,"bet",A,B)	loi bêta
grand(m,n,"bin",N,p)	loi binomiale
grand(m,n,"chi",N)	loi du chi-deux
grand(m,n,"def")	loi uniforme sur $[0,1]$
grand(m,n,"exp",M)	loi exponentielle
grand(m,n,"f",M,N)	loi de Fisher
grand(m,n,"gam",A,L)	loi gamma
grand(m,n,"lgi")	loi uniforme sur $\{0,\ldots,2^{31}\}$
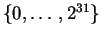grand(n,"mn",M,S)	loi normale multidimensionnelle
grand(n,"markov",P,x0)	chaîne de Markov
grand(n,"mul",N,P)	loi multinomiale
grand(m,n,"nbn",N,p)	loi binomiale négative
grand(m,n,"nch",N,x0)	loi du chi-deux décentrée
grand(m,n,"nf",M,N,x0)	loi de Fisher décentrée
grand(m,n,"nor",M,S)	loi normale unidimensionnelle
grand(m,n,"poi",L)	loi de Poisson
grand(m,"prm",V)	permutations aléatoires de V
grand(m,n,"uin",A,B)	entiers uniformes entre A et B
grand(m,n,"unf",A,B)	réels uniformes entre A et B

Section : Statistiques en Scilab
Précédent : Lois discrètes
Suivant : Représentations graphiques.