Section : Calcul numérique
Précédent : Intégration
Suivant : Equations différentielles
Résolutions et optimisation
La fonction fsolve résout numériquement un système d'équations,
mis sous la forme 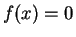 . Comme toutes les résolutions numériques,
celle-ci part d'une valeur initiale
. Comme toutes les résolutions numériques,
celle-ci part d'une valeur initiale 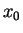 , et itère une suite censée
converger vers une solution. Le résultat dépend évidemment de la
valeur initiale.
, et itère une suite censée
converger vers une solution. Le résultat dépend évidemment de la
valeur initiale.
deff("y=f(x)","y=sin(%pi*x)")
fsolve(0.2,f)
fsolve(0.4,f)
fsolve(0.45,f)
fsolve(0.5,f)
fsolve([0.45:0.01:0.5],f)
help fsolve
[x,v,info]=fsolve(0.5,f)
[x,v,info]=fsolve([0.45:0.01:0.5],f)
| Résolutions |
fsolve |
systèmes d'équations |
roots |
racines d'un polynôme |
factors |
facteurs irréductibles réels d'un polynôme |
linsolve |
systèmes linéaires |
La fonction optim recherche un minimum (local) d'une fonction dont on
connaît le gradient. La définition de la fonction en entrée est un peu
particulière. Le choix de trois algorithmes
différents est offert en option.
help optim
deff("[y,yprim,ind]=f(x,ind)","y=sin(%pi*x),yprim=%pi*cos(%pi*x)")
[x,v]=optim(f,0.2)
[v,xopt]=optim(f,0.50000000000000001)
[v,xopt]=optim(f,0.5000000000000001)
| Optimisation |
optim |
optimisation |
linpro |
programmation linéaire |
quapro |
programmation quadratique |
© B. Ycart (2001)