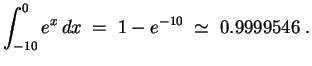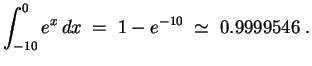Section : Calcul numérique
Précédent : Algèbre linéaire
Suivant : Résolutions et optimisation

Intégration

Des fonctions d'intégration numérique sont disponibles pour les fonctions réelles et complexes, à une, deux et trois variables. Les fonctions integrate, intg, int2d, int3d, intc et intl prennent en entrée une fonction externe, ou définie par une chaîne de caractères. Les fonctions integ, inttrap et intsplin prennent en entrée des vecteurs d'abscisses et d'ordonnées.

Calculs d'intégrales
integrate	fonction définie par une chaîne de caractères
intg	fonction externe
integ	vecteurs d'abscisses et d'ordonnées
inttrap	méthode des trapèzes
intsplin	approximation par splines
int2d	fonction de deux variables
int3d	fonction de trois variables
intc	fonction complexe le long d'un segment
intl	fonction complexe le long d'un arc de cercle

Dans l'exemple ci-dessous, on calcule avec les différentes fonctions d'intégration disponibles, la valeur de :

$$\int_{-10}^0 e^x\,dx\;=\;1-e^{-10}\;\simeq\;0.9999546\;.$$

x = [-10:0.1:0];
y=exp(x);
1-1/%e^10
inttrap(x,y)
intsplin(x,y)
integ(y,x)
integrate("exp(x)","x",-10,0)
deff("y=f(x)","y=exp(x)")
intg(-10,0,f)

Les algorithmes de calcul numérique des transformées classiques sont disponibles. Le tableau ci-dessous en donne quelques-unes, voir apropos transform pour les autres.

Transformées
dft	transformée de Fourier discrète
fft	transformée de Fourier rapide
convol	produit de convolution
flt	transformée de Legendre rapide
dmt	transformée de Mellin discrète
cwt	transformée en ondelette continue

Section : Calcul numérique
Précédent : Algèbre linéaire
Suivant : Résolutions et optimisation