
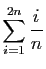 est une somme de Riemann associée à
est une somme de Riemann associée à
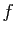 sur
sur 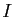 .
.
-
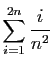 est une somme de Riemann associée à
est une somme de Riemann associée à
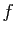 sur
sur 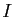 .
.

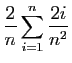 est une somme de Riemann associée à
est une somme de Riemann associée à
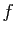 sur
sur 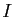 .
.
-
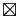
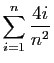 est une somme de Riemann associée à
est une somme de Riemann associée à
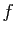 sur
sur 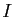 .
.

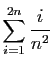 tend vers
tend vers
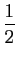 quand
quand 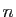 tend
vers l'infini.
tend
vers l'infini.
-
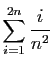 tend vers
tend vers 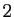 quand
quand 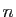 tend
vers l'infini.
tend
vers l'infini.
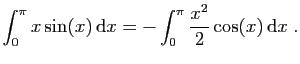
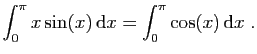
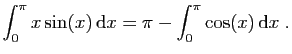
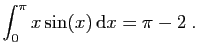
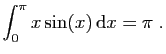
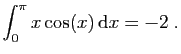
![$ \displaystyle{
\int_0^\pi x\sin(2x) \mathrm{d}x = \Big[\sin(2x)\Big]_0^\pi
-2\int_0^\pi \cos(2x) \mathrm{d}x\;.
}$](img396.gif)
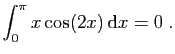
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales