Soit ![]() un réel quelconque.
Ecrivons que la suite
un réel quelconque.
Ecrivons que la suite
![]() n'est pas majorée par
n'est pas majorée par ![]() .
.
Soit ![]() un réel quelconque.
Ecrivons que la suite
un réel quelconque.
Ecrivons que la suite
![]() n'est pas majorée par
n'est pas majorée par ![]() .
.
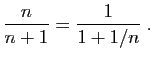
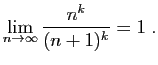
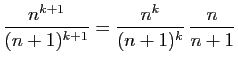
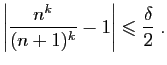
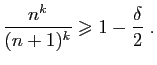
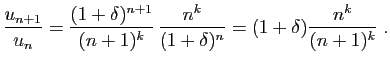
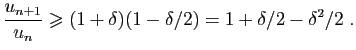
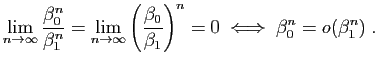
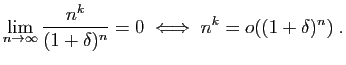
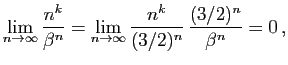
Pour la dernière relation de comparaison, écrivons :
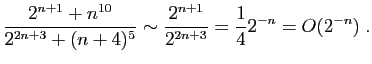
 |
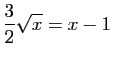 |
||
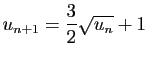 et
et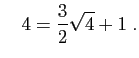
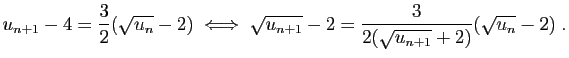
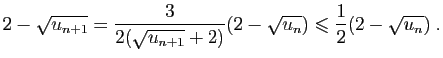
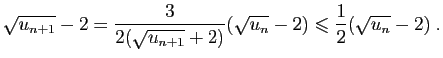
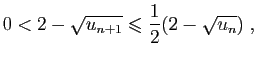
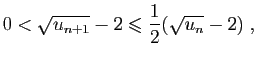
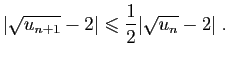
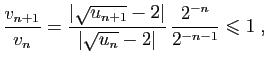
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales