De Zénon d'Élée à von Neumann

Qu'une somme de termes en nombre infini puisse donner un résultat fini intrigue depuis longtemps, au moins depuis Zénon d'Élée (v. 480-420 av. J.C.). Ses textes originaux ne nous sont pas parvenus, mais nous connaissons quelques uns de ses fameux paradoxes, par la discussion qu'en fait Aristote (384-322 av. J.C.) dans sa Physique, «le livre fondamental de la philosophie occidentale » selon Heidegger. Voici comment Aristote énonce le paradoxe «de dichotomie»

Si sur une grandeur $d$, on prend la moitié, puis la moitié de la moitié puis encore la moitié du reste, et ainsi de suite sans limitation de divisions, la grandeur obtenue en additionnant une moitié de chaque division successive (division appelée dichotomie) ne pourra jamais être égale exactement à la distance $d$. Avant d'arriver à son but, un mobile doit arriver à la moitié de son parcours. Mais auparavant, il doit arriver à la moitié de la moitié... Le mobile doit parcourir une quantité infinie d'unités d'espace. Il n'arrivera donc jamais à son but.

Pour autant, vous n'avez pas été choqués d'apprendre que

$$1=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\cdots = \sum_{n=1}^{+\infty} \frac{1}{2^n}\;.$$

Voici maintenant comment Aristote énonce le «paradoxe d'Achille et de la tortue¹».

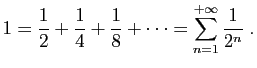
Le plus lent ne sera jamais rattrapé à la course par le plus rapide ; car il est nécessaire que le poursuivant gagne d'abord le point d'où a pris son départ le poursuivi, en sorte qu'il est nécessaire que le plus lent, à chaque fois, ait quelque avance.

Il n'est question ni d'Achille ni de tortue. Achille était probablement présent dans la version originale, par référence au passage suivant de l'Iliade d'Homère.

Ainsi qu'un homme dans un rêve n'arrive pas à poursuivre un fuyard et que celui-ci à son tour ne peut pas plus le fuir, que l'autre le poursuivre ; ainsi Achille en ce jour n'arrive pas plus à atteindre Hector à la course, qu'Hector à lui échapper.

Selon Aristote, «parcourir l'infini est impossible» : voyons cela. Disons que l'avance d'Hector (qui n'est devenu officiellement tortue qu'un bon millénaire après Zénon) est de 1 km, que sa vitesse en km/h est $v$, alors que la vitesse du «bouillant Achille» est $V>v$. Il y a deux manières de calculer. La plus simple est d'égaler $Vt$ et $vt+1$ pour trouver l'instant du contact : $1/(V-v)$. La manière compliquée est celle du paradoxe : à l'instant $1/V$, Achille est arrivé au point de départ d'Hector, mais Hector est $v/V$ plus loin. Il faut $v/V^2$ à Achille pour le rejoindre, mais il est déjà $v^2/V^2$ km plus loin, etc. L'instant de contact est donc :

$$\frac{1}{V}+\frac{v}{V^2}+\frac{v^2}{V^3}+\cdots = \frac{1}{V} \s... ...\frac{v}{V}\right)^n = \frac{1}{V} \frac{1}{1-\frac{v}{V}} = \frac{1}{V-v}\;.$$

Voici la même énigme, proposée en juin 1760 dans le volume 29 du «London magazine, or gentleman's intelligencer». Achille s'est changé en oie et la tortue en grenouille.

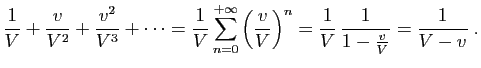
Suppose a goose and a frog to start for a wager. Let the goose give the frog one mile start; and let the goose be supposed to run ten times as fast as the frog. When will the goose overtake the frog ? I answer, if mathematics are built on a solid foundation, the goose will never overtake the frog; which I prove thus:- While the goose is running the mile that he has given the frog start, the frog will have run $\frac{1}{10}$ of a mile beyond; and while the goose runs this $\frac{1}{10}$ of a mile, the frog will have run $\frac{1}{100}$ part of a mile. While the goose is running this $\frac{1}{100}$ part of a mile, the frog must have kept his lead $\frac{1}{1000}$ part of a mile; and thus forward $\frac{1}{10000}$, $\frac{1}{100000}$, $\frac{1}{1000000}$, etc. in infinitum. Thus I prove, from strict mathematical demonstration that the goose would, in this case, never overtake the frog; - yet I know, from experience, that the goose would really overtake the frog in a small space of running. Do mathematics then contradict facts, which is the touchstone of all science?

Les mathématiciens, anglais en particulier, manipulaient déjà les séries infinies depuis un bon siècle. Le mois suivant, la réponse est publiée.

The human mind, being finite, cannot comprehend infinity; and so a solution to the query concerning the Goose and the Frog cannot be given in the manner requested by your correspondent.

[...]

An hour is equal to $59'$, $59''$, $59'''$ etc. ad infinitum. If, therefore, a body, that by an equable motion would require an hour to run over a certain space, were to move so much thereof as would require $59'$, and then as much as would require $59''$, and then so much more as would require $59'''$, etc., reason can no other way account for the completion of the hour's journey, by that body, than by considering its motion in another light than as being made up of an infinite series. In fine, when any thing is proposed for a solution, that is within the reach of our finite capacity, then Mathematicks, noble, unerring, universally-useful Mathematicks, lend their amicable and infallible assistance towards a solution thereof.

Puisque vous voilà disposés à profiter de l'«amicable and infallible assistance» des mathématiques, voici une version moderne du même casse-tête.

Un train part de la ville A à 60 km/h pour se rendre à la ville B, distante de 120 km, et en même temps un train part de B vers A à la même vitesse. Toujours au même instant, une mouche décolle du pare-brise du train A en direction de B, à une vitesse double de celle des trains; lorsque la mouche rencontre le train B elle fait instantanément demi-tour, puis de même lorsqu'elle rencontre à nouveau le train A et ainsi de suite. Sachant que les deux trains circulent sur la même voie, quelle distance aura parcouru la mouche avant de périr dans l'accident final ?

Là encore deux manières de calculer. La simple : les trains roulent pendant une heure, la mouche vole pendant le même temps, elle parcourt donc 120 km. Et puis la compliquée : quelle distance la mouche parcourt-elle pour rejoindre le train qui roule en sens inverse, puis quelle distance parcourt-elle dans son trajet de retour... Sommez la série, vous devez trouver la même chose.

Voici ce que raconte McRae dans sa biographie de von Neumann (1903-1957)². Les trains sont des bicyclettes, ce qui permet à la pauvre mouche, si elle n'échappe pas à son destin funeste, de voler à une vitesse plus raisonnable.

When he was given a problem while standing, Johnny at one stage would dance from foot to foot. Although this practice caused some spills at his crowded cocktail parties, it forms one of the first stories half against him: his reaction to the fly puzzle. Two cyclists are 20 miles apart and head toward each other at 10 miles per hour each. At the same time a fly traveling at a steady 15 miles per hour starts from the front wheel of the northbound bicycle. It lands on the frontwheel of the southbound bicycle, and then instantly turns around and flies back, and after next landing instantly flies north again. Question: What total distance did the fly cover before it was crushed between the two front wheels?

The slow way of answering is to calculate the distance that the fly travels on its first trip to the southbound front wheel, then the distance it travels on its next trip to the northbound wheel, and finally to sum the infinite series so obtained. It is extraordinary how many mathematicians can be fooled into doing that long sum. The short way is to note that the bicycles will meet exactly one hour after starting, by which time the 15-miles-per-hour fly must have covered 15 miles. When the question was put to Johnny, he danced and anwered immediately, ``15 miles''. ``Oh, you've heard the trick before'' daid the disappointed questioner. ``What trick?'' asked the puzzled Johnny. ``I simply summed the infinite series.'' It is worth adding that, when ribbed on this later, Johnny said ``the figures actually put to me were not so simple''.

L'anecdote est plaisante, mais un peu difficile à croire, s'agissant du «most scintillating intellect of the century» (selon Peter Lax).