 Si la série
Si la série 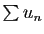 converge, alors la série
converge, alors la série
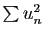 converge.
converge.
-
 Si la série
Si la série 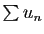 est absolument convergente,
alors la série
est absolument convergente,
alors la série
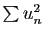 converge.
converge.
 Si la série
Si la série 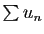 converge, alors la série
converge, alors la série
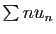 converge.
converge.
 Si les séries
Si les séries 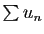 et
et 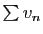 divergent, alors la série
divergent, alors la série
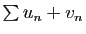 diverge.
diverge.
-
 Si la série
Si la série 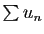 converge, alors la série
converge, alors la série
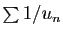 diverge.
diverge.
 Si la série
Si la série 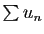 converge, alors la série
converge, alors la série
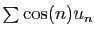 converge.
converge.
-
 Si la série
Si la série 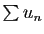 est absolument convergente,
alors la série
est absolument convergente,
alors la série
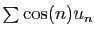 converge.
converge.
-
 Si la série
Si la série
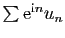 est absolument convergente,
alors la série
est absolument convergente,
alors la série
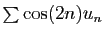 converge.
converge.
-
 Un nombre réel
Un nombre réel ![$ x\in[0,1]$](img384.gif) dont toutes les décimales sont strictement
positives est supérieur à
dont toutes les décimales sont strictement
positives est supérieur à
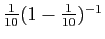 .
.
 Un nombre réel
Un nombre réel ![$ x\in[0,1]$](img384.gif) dont toutes les décimales sont égales
à
dont toutes les décimales sont égales
à 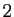 ou à
ou à 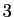 est compris entre
est compris entre
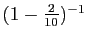 et
et
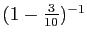 .
.
-
 Si
Si 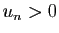 pour tout
pour tout 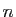 et
et 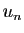 est équivalent à
est équivalent à
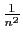 quand
quand 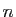 tend vers l'infini, alors
tend vers l'infini, alors
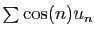 converge.
converge.
 Si
Si 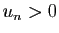 pour tout
pour tout 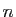 et
et 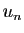 est équivalent à
est équivalent à
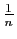 quand
quand 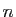 tend vers l'infini, alors
tend vers l'infini, alors
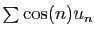 converge.
converge.
 Si
Si 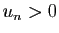 pour tout
pour tout 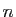 et si la suite
et si la suite 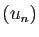 est décroissante,
alors
est décroissante,
alors
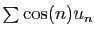 converge.
converge.
-
 Si la suite
Si la suite 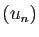 est décroissante et tend vers 0,
alors
est décroissante et tend vers 0,
alors
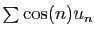 converge.
converge.
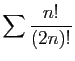
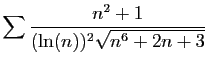
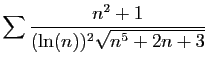
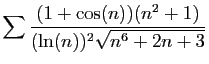
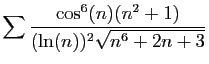
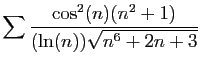
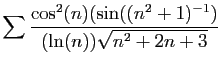
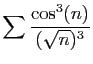

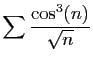
![$ \displaystyle{
\sum \frac{\cos^3(n)}{\sqrt{n}\sqrt[6]{n^2+n}}
}$](img415.gif)
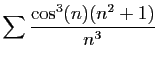
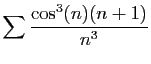
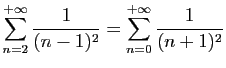
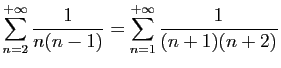
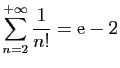
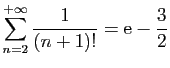
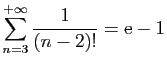
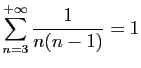
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales