-
 Si
Si 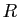 est le rayon de convergence de la série
est le rayon de convergence de la série
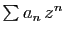 ,
alors la suite
,
alors la suite
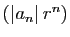 tend vers 0, pour tout
tend vers 0, pour tout 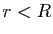 .
.
 Si
Si 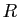 est le rayon de convergence de la série
est le rayon de convergence de la série
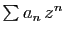 ,
alors la suite
,
alors la suite
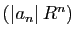 est bornée.
est bornée.
 Si
Si
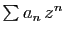 converge, alors son rayon de convergence est le
module de
converge, alors son rayon de convergence est le
module de 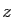 .
.
-
 Si
Si
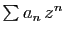 converge mais n'est pas absolument convergente,
alors son rayon de convergence est le module de
converge mais n'est pas absolument convergente,
alors son rayon de convergence est le module de 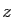 .
.
-
 Si
Si
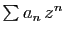 converge alors son rayon de convergence est
supérieur ou égal au module de
converge alors son rayon de convergence est
supérieur ou égal au module de 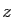 .
.
 Si
Si
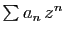 diverge alors son rayon de convergence est
strictement inférieur au module de
diverge alors son rayon de convergence est
strictement inférieur au module de 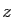 .
.
 Si le rayon de convergence de
Si le rayon de convergence de
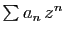 est
est 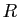 et si
et si 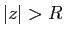 ,
alors la suite
,
alors la suite
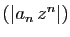 tend vers
tend vers 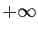 .
.
-
 Les rayons de convergence de
Les rayons de convergence de
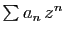 et
de
et
de
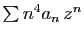 sont égaux.
sont égaux.
 Si le rayon de convergence de
Si le rayon de convergence de
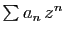 est
est  ,
alors le rayon de convergence de
,
alors le rayon de convergence de
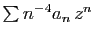 est
strictement supérieur à
est
strictement supérieur à 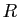 .
.
-
 Si la suite
Si la suite 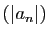 ne prend qu'un nombre fini de valeurs non
nulles, alors le rayon de convergence de
ne prend qu'un nombre fini de valeurs non
nulles, alors le rayon de convergence de
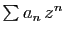 est
est 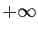 .
.
 Si le rayon de convergence de
Si le rayon de convergence de
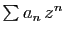 est
est 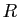 , alors le rayon
de convergence de
, alors le rayon
de convergence de
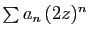 est
est 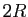 .
.
 Si le rayon de convergence de
Si le rayon de convergence de
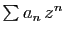 est
est 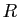 , alors le rayon
de convergence de
, alors le rayon
de convergence de
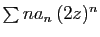 est strictement inférieur
à
est strictement inférieur
à 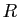 .
.
-
 Si le rayon de convergence de
Si le rayon de convergence de
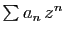 est
est 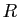 , alors le rayon
de convergence de
, alors le rayon
de convergence de
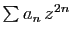 est
est 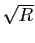 .
.
 Si le rayon de convergence de
Si le rayon de convergence de
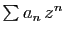 est
est 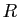 , et si
, et si 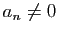 pour tout
pour tout 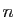 , alors le rayon
de convergence de
, alors le rayon
de convergence de
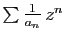 est
est
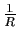 .
.
-
 Les séries
Les séries
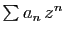 et
et
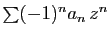 ont le même
rayon de convergence.
ont le même
rayon de convergence.
 Pour tout
Pour tout
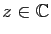 , la série
, la série
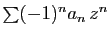 converge si et
seulement si la
série
converge si et
seulement si la
série
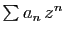 converge.
converge.
 Si la série
Si la série
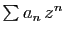 a un rayon de convergence infini,
alors elle converge uniformément sur
a un rayon de convergence infini,
alors elle converge uniformément sur
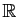 .
.
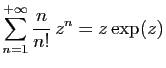
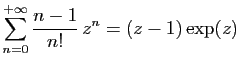
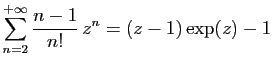
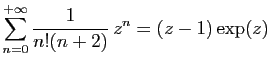
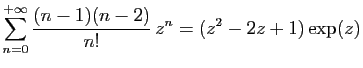
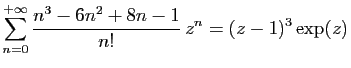
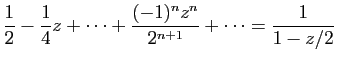
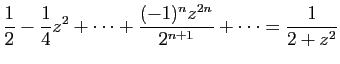
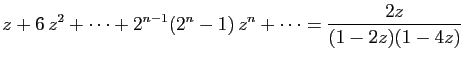
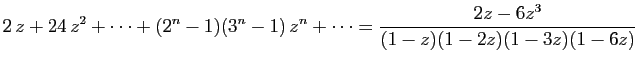
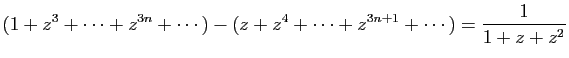
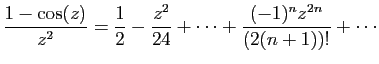
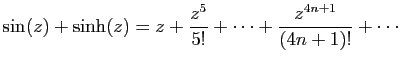
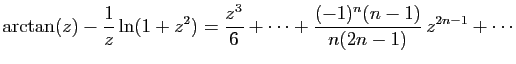
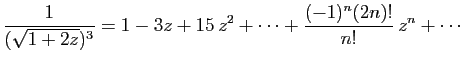
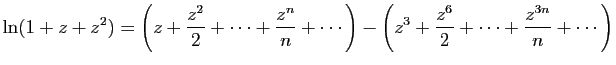
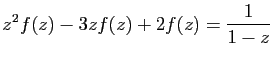
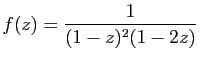
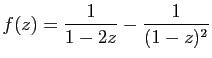
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales