Produits infinis

Étendre aux développements en séries entières les propriétés des polynômes était une des astuces favorites d'Euler. Dans la même logique, connaissant les zéros d'une fonction, qui oserait l'empêcher d'écrire cette fonction comme un produit de monômes ? Par exemple, les valeurs de $x$ qui annulent $\sin x$ sont les $k\pi$, pour tout $k\in\mathbb{Z}$. On peut donc s'attendre à retrouver dans $\sin x$ un facteur $x$ et pour tout $n\in\mathbb{N}^*$, deux facteurs $(x-k\pi)$ et $(x+k\pi)$, soit encore un facteur proportionnel à $\left(x^2-k^2\pi^2\right)$. Il se trouve que ça marche, et la formule porte même le nom de «produit d'Euler».

$$\sin(x)=x\prod_{k=1}^{+\infty}\left(1-\frac{x^2}{\pi^2k^2}\right)\;.$$

N'en déduisez pas pour autant qu'il suffit d'écrire n'importe quoi d'intuitivement justifiable pour que ce soit mathématiquement correct. Voici comment débute le «Mémoire sur l'application du calcul des résidus à l'évaluation et à la transformation des produits composés d'un nombre infini de facteurs» lu par Cauchy à l'Académie des Sciences le 31 août 1829.

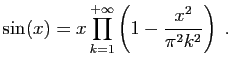
On sait qu'une fonction entière de la variable $x$ peut toujours être décomposée en facteurs linéaires qui, égalés séparément à zéro, fournissent les diverses racines de l'équation algébrique, dont le premier membre serait précisément la fonction dont il s'agit. Cette propriété des fonctions entières subsiste pour quelques fonctions transcendantes. Ainsi, par exemple, $\sin x$ et $\cos x$ sont décomposables en facteurs linéaires, qui, égalés séparément à zéro, fournissent les diverses racines des équations $\sin x=0$, $\cos x=0$. Mais on se tromperait si l'on attribuait la propriété ci-dessus énoncée à toute espèce de fonctions, et il peut arriver que le produit $P$ de tous les facteurs linéaires correspondant aux différentes valeurs de $x$, pour lesquels une fonction transcendante s'évanouit, ne soit pas équivalent ni même proportionnel à cette fonction. Ainsi, en particulier, les seules valeurs de $x$, propres à faire évanouir la fonction $\mathrm{e}^x-1$ sont comprises dans les formules

$$x=0\qquad x=\pm n\pi\sqrt{-1}\;,$$

$n$ étant un nombre entier quelconque, et cependant le produit $P$ de $x$ par tous les facteurs linéaires de la forme

$$1\pm \frac{x}{n\pi\sqrt{-1}}$$

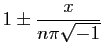
n'est pas équivalent ni même proportionnel à $\mathrm{e}^x-1$. Mais on a dans ce cas

$$\mathrm{e}^x-1=P\mathrm{e}^{\frac{x}{2}}\;,$$

en sorte que, pour obtenir la fonction transcendante $\mathrm{e}^x-1$ il faut multiplier le produit $P$ par un nouveau facteur $\mathrm{e}^{\frac{x}{2}}$ qui n'est point linéaire, ni décomposable en facteurs linéaires déterminés, et qui ne s'évanouit pour aucune valeur finie de la variable $x$. On voit donc que les principes qui servent de base à la décomposition des fonctions entières en facteurs linéaires, ne sauraient s'appliquer aux fonctions transcendantes.

Tant valait que ce soit dit !