Le binôme de Newton

Voici ce qu'écrivait Abel en 1826.

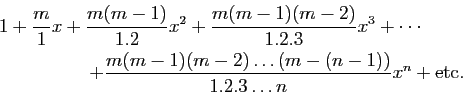
Une des séries les plus remarquables dans l'analyse algébrique est celle-ci :

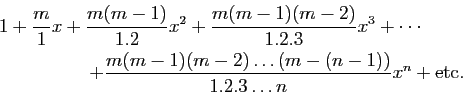
$\begin{displaymath} \begin{array}{l} \displaystyle{ 1+\frac{m}{1}x+\frac{m(m-1)}... ...-2)\ldots(m-(n-1))}{1.2.3\ldots n} x^n+\mbox{etc}.} \end{array}\end{displaymath}$

Lorsque est un nombre entier positif, on sait que la somme de cette série, qui dans ce cas est finie, peut s'exprimer par . Lorsque n'est pas un nombre entier, la série ira à l'infini, et elle sera convergente ou divergente, selon les différentes valeurs qu'on attribue à et . Dans ce cas on pose de même l'équation

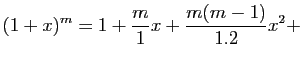$\displaystyle (1+x)^m=1+\frac{m}{1}x+\frac{m(m-1)}{1.2}x^2+$ etc $\displaystyle .$

mais alors l'égalité exprime seulement que les deux expressions

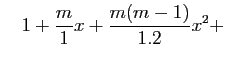$\displaystyle (1+x)^m$ et $\displaystyle \quad 1+\frac{m}{1}x+\frac{m(m-1)}{1.2}x^2+$ etc $\displaystyle .$

ont certaines propriétés communes desquelles, pour certaines valeurs de et de , dépend l'égalité des valeurs numériques des expressions. On suppose que l'égalité numérique aura toujours lieu, lorsque la série est convergente ; mais c'est ce qui jusqu'à présent n'est pas encore démontré. On n'a pas même examiné tous les cas où la série est convergente. Lors même qu'on suppose l'existence de l'équation ci-dessus, il reste pourtant à chercher la valeur de , car cette expression a en général une infinité de valeurs différentes, tandis que la série etc. n'en a qu'une.

Le but de ce mémoire est d'essayer de remplir une lacune par la résolution complète du problème suivant :

«Trouver la somme de la série

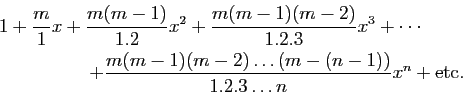
$\begin{displaymath} \begin{array}{l} \displaystyle{ 1+\frac{m}{1}x+\frac{m(m-1)}... ...-2)\ldots(m-(n-1))}{1.2.3\ldots n} x^n+\mbox{etc}.} \end{array}\end{displaymath}$

pour toutes les valeurs réelles ou imaginaires de et de pour lesquelles la série est convergente.

Et effectivement, pour la première fois depuis un siècle et demi, la formule du binôme était correctement démontrée, en toute généralité. Abel n'était pas le premier à constater le manque de rigueur des traitements antérieurs. Les premiers articles démontrant correctement des convergences sont ceux de Gauss en 1812 pour la série hypergéométrique puis Bolzano en 1816, également pour la série binomiale. Fervents lecteurs de compléments comme nous vous savons, vous n'ignorez pas que la «formule de Newton» pour un exposant entier était connue des mathématiciens de la Renaissance ; avant eux des arabes, avant eux des chinois... et avant eux des indiens. La réussite de Newton est de l'avoir étendue aux exposants rationnels, positifs ou négatifs. Pour Newton, la formule était plus un algorithme d'approximation qu'une série entière à notre sens. Il n'était pas question bien sûr de convergence, et la condition $\vert x\vert<1$ restait implicite. Il est difficile de savoir si Newton était bien le premier : la première publication de la formule n'est pas de lui mais de James Gregory, en 1670. Newton assura plus tard qu'il s'agissait d'un de ses tous premiers travaux mathématiques, élaboré à partir de l'Arithmerica Infinitorum de John Wallis¹. Encore une production de ces deux années magiques entre l'été 1665 et la rentrée 1667, où retiré à la campagne à cause de l'épidémie de peste qui avait entraîné la fermeture des universités, il avait découvert rien moins que le calcul différentiel, le télescope à réflexion, la gravitation universelle et la composition de la lumière.