Hamilton et les quaternions

On peut voir l'ensemble $\mathbb{C}$ des nombres complexes comme l'ensemble $\mathbb{R}^{2}$ des couples de nombres réels, en identifiant $a+\mathrm{i}b$ et $(a,b)$. La multiplication dans $\mathbb{C}$ correspond alors à une façon de multiplier les couples de nombres réels :

$$(a,b)\cdot(c,d)=(ac-bd,ad+bc).$$

Ce point de vue a été développé en 1835 par William Hamilton. Par la suite, il essaya longuement et sans succès de multiplier des triplets de nombres réels de façon satisfaisante mais il finit par réussir à multiplier des quadruplets, inventant ainsi en 1843 l'ensemble des quaternions, noté $\mathbb{H}$ en son honneur.

Sir William Rowan Hamilton (1805-1865), né à Dublin, fut à la fois un enfant adopté et un enfant surdoué. À 13 ans, il parlait autant de langues que le nombre de ses années : bien sûr la plupart des langues européennes mais aussi les langues persane, arabe, hindoue, malaise, et le sanskrit. Il resta toute sa vie au Trinity College de Dublin, où il avait été nommé professeur d'astronomie à l'âge de 22 ans. Calculateur génial, il semble avoir pris grand plaisir toute sa vie durant à effectuer des multiplications monstrueuses. À 10 ans, il découvre par accident une copie en latin des Éléments d'Euclide et à 12 ans il dévore les Principia de Newton. Pendant l'été 1822, à 17 ans, il étudie de manière systématique la Mécanique céleste de Laplace et y trouve une faute sérieuse, qu'il réussit à corriger. Hamilton décide alors de se consacrer principalement aux mathématiques, ce qui ne l'empêchera pas de fournir également d'importantes contributions en optique et en mécanique.

Figure 3: Broom Bridge à Dublin

Le but de Hamilton était donc d'étendre les propriétés des nombres complexes à des dimensions supérieures, essentiellement sans succès. D'ailleurs Frobenius démontrera en 1877 qu'une telle structure ne pouvait pas exister pour l'ensemble des triplets. Hamilton racontera plus tard que, dans la soirée du 16 octobre 1843, il marchait le long du Canal royal de Dublin avec sa femme, en route vers une soirée, quand la solution pour des quadruplets lui apparut soudain, sous la forme

$$\mathrm{i}^{2}=\mathrm{j}^{2}=\mathrm{k}^{2}=\mathrm{i}\mathrm{j}\mathrm{k}=-1,$$

et qu'il grava aussitôt ces équations au couteau dans une pile du pont le plus proche, Broom Bridge. Depuis 1989, la National University d'Irlande organise un pèlerinage depuis l'observatoire de Dunsink où Hamilton travaillait jusqu'à ce pont où malheureusement, aucune trace de la formule gravée en 1843 ne demeure (par contre une plaque commémore le geste de Hamilton).

Hamilton aboutit aux quaternions en imposant de respecter la multiplication des modules et en conservant l'associativité mais, geste révolutionnaire pour l'époque, en abandonnant la commutativité. Pour présenter l'algèbre $\mathbb{H}$ en termes modernes, rappelons que le corps $\mathbb{C}$ des nombres complexes peut être représenté par l'algèbre des matrices à coefficients réels de la forme

$$\left(\begin{array}{rr}a & -b \\ b & a\end{array}\right).$$

Une façon de le voir est de représenter le nombre complexe $a+b\mathrm{i}$ par la transformation de $\mathbb{C}$ dans $\mathbb{C}$ définie par $z\mapsto(a+b\mathrm{i})\cdot z$, transformation $\mathbb{R}$-linéaire dont la matrice dans la base $(1,\mathrm{i})$ de l'espace vectoriel $\mathbb{C}$ sur $\mathbb{R}$ est précisément la matrice ci-dessus.

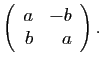
De même on représente un quaternion par une matrice complexe

$$\left(\begin{array}{rr}a+b\mathrm{i}& -c-d\mathrm{i}\\ c-d\mathrm{i}& a-b\mathrm{i}\end{array}\right).$$

Cette fois, on considère la base $(1,\mathrm{j})$ de l'espace vectoriel complexe $\mathbb{H}$ et il s'agit de la matrice dans cette base de la transformation de $\mathbb{H}$ dans $\mathbb{H}$ définie par

$$h\mapsto ((a+b\mathrm{i})+(c+d\mathrm{i})\cdot\mathrm{j})\cdot h.$$

En effet, les formules de Broom Bridge impliquent également les relations

$$\mathrm{i}\mathrm{j}=\mathrm{k},\ \mathrm{i}\mathrm{k}=-\mathrm{... ...hrm{i},\ \mathrm{k}\mathrm{i}=\mathrm{j},\ \mathrm{k}\mathrm{j}=-\mathrm{i},$$

ce qui permet de compléter la «table de multiplication»  de $\{1,\mathrm{i},\mathrm{j},\mathrm{k}\}$. Tout quaternion $h$ peut donc s'écrire comme une combinaison linéaire à coefficients réels des vecteurs de la base $(1,\mathrm{i},\mathrm{j},\mathrm{k})$ de $\mathbb{H}$ sur $\mathbb{R}$, soit $h=a+b\mathrm{i}+c\mathrm{j}+d\mathrm{k}$ avec $(a,b,c,d)\in\mathbb{R}^{4}$, ou bien comme une combinaison linéaire à coefficients complexes des vecteurs de la base $(1,\mathrm{j})$ de $\mathbb{H}$ sur $\mathbb{C}$, soit $h=z+w\mathrm{j}$ avec $(z,w)\in\mathbb{C}^{2}$.

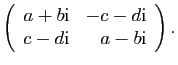
Il est essentiel ici de considérer $\mathbb{H}$ comme un espace vectoriel sur $\mathbb{C}$ à droite sinon la multiplication ainsi définie n'est pas $\mathbb{C}$-linéaire. En particulier, pour identifier la première colonne, on utilisera la relation

$$(a+b\mathrm{i})+(c+d\mathrm{i})\mathrm{j}=(a+b\mathrm{i})+\mathrm{j}(c-d\mathrm{i}).$$

Cette découverte démontra la nécessité de travailler aussi avec des lois non commutatives, une avancée radicale pour l'époque. Il faut se rappeler que vecteurs et matrices faisaient encore partie du futur, mais Hamilton venait en quelque sorte d'introduire avant l'heure le produit vectoriel et le produit scalaire des vecteurs.

On sait à présent que bien avant Hamilton, en 1748, le mathématicien et physicien suisse Leonhard Euler (1707-1783) connaissait la règle de multiplication des quaternions, sous la forme du théorème des quatre carrés, ainsi que le mathématicien, astronome et physicien allemand Carl Friedrich Gauss (1777-1855) en 1819. Hamilton quant à lui passa le reste de sa vie à explorer cette notion car il pensait que sa découverte allait révolutionner la physique mathématique. La postérité démentit ce pronostic et porta un regard souvent sévère sur son invention. D'après le physicien mathématicien et ingénieur écossais William Thomson alias Lord Kelvin (1824-1907) par exemple (oui, le Kelvin des degrés Kelvin) :

Quaternions came from Hamilton after his really good work had been done, and though beautifully ingenious, have been an unmixed evil to those who have touched them in any way.