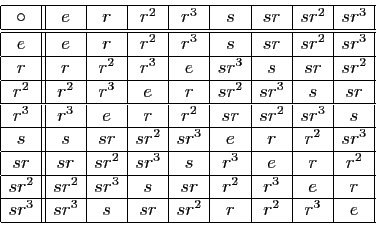
- réflexive :
Soit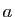 un élément de
un élément de 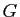 . Le produit
. Le produit 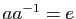 appartient à
appartient à
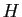 (tout sous-groupe de
(tout sous-groupe de 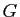 contient l'élément neutre). Donc
contient l'élément neutre). Donc
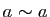 .
.
- symétrique :
Soient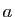 et
et 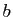 deux éléments de
deux éléments de 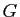 . Supposons
. Supposons 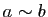 . Alors
. Alors
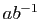 appartient à
appartient à 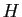 .
Donc l'inverse de
.
Donc l'inverse de 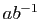 appartient aussi à
appartient aussi à 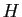 . Or cet inverse
est
. Or cet inverse
est
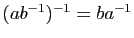 . Donc
. Donc 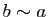 .
.
- transitive :
Soient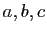 trois éléments de
trois éléments de 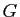 . Supposons
. Supposons 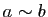 et
et
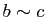 . Les deux éléments
. Les deux éléments 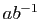 et
et 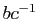 appartiennent
à
appartiennent
à 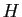 , donc leur produit aussi. Ce produit est :
, donc leur produit aussi. Ce produit est :
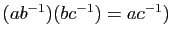 . Donc
. Donc 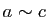 .
.
Montrons que ![]() est injective. Soient
est injective. Soient ![]() et
et ![]() deux
éléments de
deux
éléments de ![]() tels que
tels que
![]() . Alors
. Alors ![]() , donc
, donc
![]() , soit
, soit ![]() .
.
L'application ![]() est donc une bijection de
est donc une bijection de ![]() dans
dans
![]() .
.
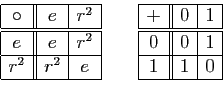
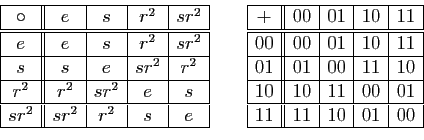

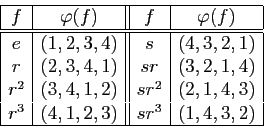
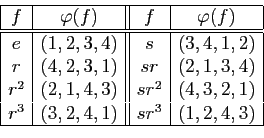
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales