Essayez de bien rédiger vos réponses, sans vous
reporter ni au cours, ni au corrigé.
Si vous souhaitez vous évaluer, donnez-vous deux heures ; puis comparez
vos réponses avec le corrigé et comptez un point pour
chaque question à laquelle vous aurez correctement répondu.
Questions de cours :
Soit 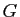 un groupe fini et
un groupe fini et 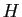 un sous-groupe de
un sous-groupe de 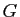 .
.
- Soit
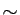 la relation définie sur
la relation définie sur 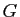 par :
par :
Montrer que 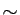 est une relation d'équivalence sur
est une relation d'équivalence sur 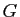 .
.
- Soit
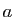 un élément de
un élément de 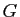 et
et 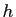 un élément de
un élément de 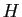 . Montrer
que
. Montrer
que 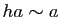 .
.
- Montrer que si
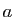 et
et 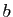 sont deux
éléments de
sont deux
éléments de 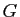 tels que
tels que 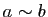 , alors il existe un
élément
, alors il existe un
élément 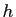 de
de 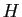 tel que
tel que 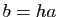 .
.
- Soit
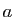 un élément quelconque de
un élément quelconque de 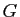 . On note
. On note
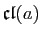 sa classe
d'équivalence pour la relation
sa classe
d'équivalence pour la relation 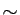 . Soit
. Soit 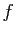 l'application qui
à un élément
l'application qui
à un élément 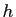 de
de 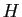 associe l'élément
associe l'élément 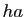 . Montrer que
. Montrer que
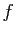 est une bijection de
est une bijection de 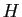 dans
dans
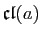 .
.
- En déduire que le cardinal de
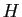 divise le cardinal de
divise le cardinal de 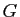 .
.
Exercice 1 :
Soient 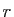 et
et 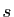 les applications de
les applications de
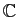 dans
lui-même définies comme suit.
dans
lui-même définies comme suit.

Dans tout l'exercice, on identifiera l'application 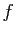 de
de
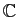 dans
dans
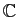 , avec l'application du plan complexe dans lui-même, qui
à un point
, avec l'application du plan complexe dans lui-même, qui
à un point 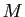 d'affixe
d'affixe 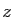 associe le point
associe le point 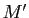 d'affixe
d'affixe 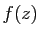 .
.
- On note
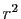 et
et 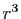 les composées
les composées
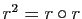 et
et
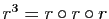 .
Interpréter comme transformations géométriques du plan complexe
les applications
.
Interpréter comme transformations géométriques du plan complexe
les applications 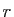 ,
, 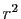 ,
, 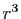 ,
, 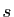 ,
, 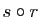 ,
,
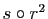 ,
,
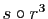 .
.
- On note
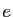 l'application indentité du plan complexe.
Montrer que l'ensemble
l'application indentité du plan complexe.
Montrer que l'ensemble
muni de la composition des applications est un groupe, dont on donnera
la table de composition. Il sera noté 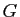 .
.
- Montrer que
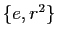 ,
, 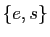 ,
,
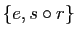 ,
,
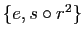 ,
,
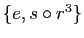 , sont des sous-groupes de
, sont des sous-groupes de 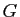 , tous isomorphes à
, tous isomorphes à
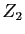 .
.
- Montrer que
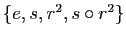 est un sous-groupe de
est un sous-groupe de 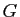 ,
isomorphe à
,
isomorphe à
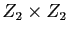 .
.
- Montrer que
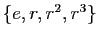 est un sous-groupe de
est un sous-groupe de 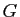 ,
isomorphe à
,
isomorphe à 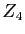 .
.
- On note :
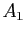 le point du plan complexe d'affixe
le point du plan complexe d'affixe
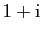 ,
,
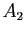 le point du plan complexe d'affixe
le point du plan complexe d'affixe
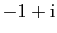 ,
,
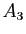 le point du plan complexe d'affixe
le point du plan complexe d'affixe
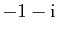 ,
,
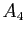 le point du plan complexe d'affixe
le point du plan complexe d'affixe
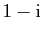 ,
,
Vérifier que chaque élément du groupe 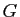 laisse invariant
l'ensemble
laisse invariant
l'ensemble
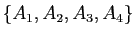 .
.
- Étant donné un élément
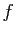 du groupe
du groupe 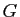 , on
lui associe la permutation
, on
lui associe la permutation
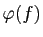 de
de
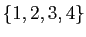 définie par :
définie par :
On définit ainsi une application 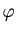 de
de 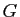 dans
dans
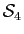 . Montrer que
. Montrer que 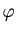 est un morphisme de groupes.
est un morphisme de groupes.
- Écrire in extenso l'image par
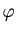 de chacun des éléments
de
de chacun des éléments
de 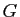 .
.
- Soit
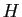 l'image de
l'image de 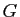 par
par 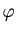 . Montrer que
. Montrer que 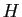 est un
sous-groupe de
est un
sous-groupe de
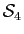 , isomorphe à
, isomorphe à 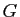 .
.
- On note :
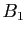 le point du plan complexe d'affixe
le point du plan complexe d'affixe
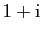 ,
,
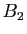 le point du plan complexe d'affixe
le point du plan complexe d'affixe
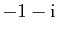 ,
,
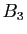 le point du plan complexe d'affixe
le point du plan complexe d'affixe
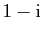 ,
,
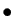
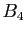 le point du plan complexe d'affixe
le point du plan complexe d'affixe
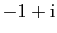 ,
,
Reprendre les questions 6, 7, 8, 9, en remplaçant
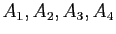 par
par
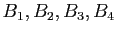 .
.
Exercice 2 :
On note 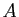 l'ensemble de réels suivant :
l'ensemble de réels suivant :
- Montrer que
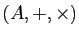 (ensemble
(ensemble 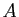 muni de l'addition et de la
multiplication des réels), est un sous-anneau de
muni de l'addition et de la
multiplication des réels), est un sous-anneau de
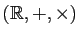 .
.
- On considère l'application
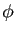 , de
, de 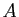 dans
lui-même, qui à
dans
lui-même, qui à
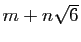 associe :
associe :
Montrer que 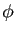 est un automorphisme de l'anneau
est un automorphisme de l'anneau
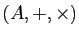 (c'est-à-dire une bijection, et un morphisme pour
chacune des deux lois).
(c'est-à-dire une bijection, et un morphisme pour
chacune des deux lois).
- Pour tout
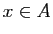 , on pose
, on pose
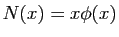 . Montrer que
. Montrer que
 est une application de
est une application de 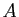 dans
dans
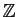 , qui est un
morphisme pour la multiplication.
, qui est un
morphisme pour la multiplication.
- Démontrer que
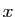 est un élément inversible de
est un élément inversible de 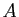 si et seulement si
si et seulement si
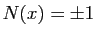 .
.
- Vérifier que
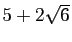 est inversible dans
est inversible dans
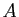 et calculer son inverse.
et calculer son inverse.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() un groupe fini et
un groupe fini et ![]() un sous-groupe de
un sous-groupe de ![]() .
.

 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales