Anneaux et corps
Il s'agit ici simplement de rajouter un peu de
vocabulaire pour pouvoir décrire
les propriétés que possèdent les
ensembles de nombres usuels. Le chapitre se
limitera donc à quelques définitions.
L'archétype de l'anneau est l'ensemble
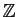 des entiers relatifs ; dans un
anneau quelconque on peut calculer «comme» dans
des entiers relatifs ; dans un
anneau quelconque on peut calculer «comme» dans
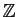 . Méfiance sur un seul
point toutefois : la définition n'exigeant pas que la multiplication soit
commutative, certaines formules peuvent être un peu plus perverses ; par
exemple
. Méfiance sur un seul
point toutefois : la définition n'exigeant pas que la multiplication soit
commutative, certaines formules peuvent être un peu plus perverses ; par
exemple 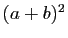 se développe en
se développe en
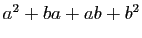 , mais ne peut pas dans un
anneau trop général être regroupé en
, mais ne peut pas dans un
anneau trop général être regroupé en
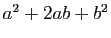 puisque
puisque 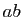 n'a aucune
raison d'être égal à
n'a aucune
raison d'être égal à 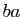 .
.
Voici un autre exemple.
Proposition 15
Soit 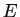 un espace vectoriel.
L'ensemble des applications linéaires de
un espace vectoriel.
L'ensemble des applications linéaires de 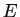 vers
vers 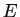 ,
noté
,
noté
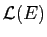 , est un anneau pour l'addition et la composition.
, est un anneau pour l'addition et la composition.
Démonstration : Les propriétés d'«anneau» sont généralement évidentes à
vérifier ; la plus intéressante est la distributivité,
qui est liée à la linéarité, et que nous laissons gentiment
au lecteur.
Le neutre pour la
composition est sans surprise l'application identique.
Si on choisit pour espace vectoriel
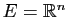 et
que l'on représente les éléments
de
et
que l'on représente les éléments
de
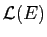 par des matrices carrées,
on obtient l'anneau
par des matrices carrées,
on obtient l'anneau
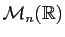 des matrices
carrées de taille
des matrices
carrées de taille 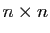 à coefficients réels.
à coefficients réels.
Le neutre de
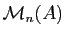 pour l'addition est la
matrice nulle, dont tous les coefficients valent
le neutre de l'addition de
pour l'addition est la
matrice nulle, dont tous les coefficients valent
le neutre de l'addition de 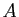 .
Le neutre de
.
Le neutre de
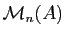 pour la multiplication est
la matrice identité, dont tous les
coefficients valent le neutre de l'addition de
pour la multiplication est
la matrice identité, dont tous les
coefficients valent le neutre de l'addition de 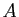 sauf ceux de la diagonale qui valent le neutre de la
multiplication de
sauf ceux de la diagonale qui valent le neutre de la
multiplication de 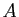 .
.
Définition 26
Un anneau est dit commutatif quand sa multiplication est
commutative.
Une classe particulière d'anneaux est celle des anneaux
tels que la deuxième loi
(la multiplication) fournit aussi une structure
de groupe (sur l'anneau privé de son zéro).
Définition 28
On dit qu'un anneau 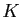 est un corps commutatif lorsque :
est un corps commutatif lorsque :
(i) La multiplication est commutative.
(ii)
L'anneau 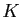 possède au moins deux éléments.
possède au moins deux éléments.
(iii)
Tout élément non nul de 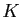 possède un inverse pour la multiplication.
possède un inverse pour la multiplication.
Les archétypes de corps commutatifs sont naturellement
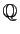 , ensemble des
fractions, et, encore mieux connus des étudiants,
, ensemble des
fractions, et, encore mieux connus des étudiants,
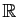 et
et
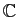 . Un autre archétype, au moins aussi
important malgré sa simplicité, est
. Un autre archétype, au moins aussi
important malgré sa simplicité, est 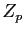 pour
pour 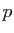 premier.
Nous avons déjà défini l'addition sur
premier.
Nous avons déjà défini l'addition sur 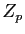 .
On définit une multiplication
.
On définit une multiplication 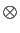 , en convenant
que
, en convenant
que
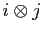 est l'unique entier
est l'unique entier
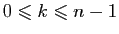 tel que
tel que
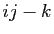 est divisible par
est divisible par 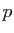 . On démontre facilement que
. On démontre facilement que
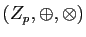 est un anneau pour tout entier
est un anneau pour tout entier 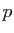 , et que
c'est un corps, si et seulement si
, et que
c'est un corps, si et seulement si 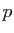 est premier.
Ces corps servent entre autres en cryptographie.
Le plus petit d'entre eux,
est premier.
Ces corps servent entre autres en cryptographie.
Le plus petit d'entre eux, 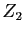 , peut être
considéré comme la base de toute l'informatique :
excusez du peu !
, peut être
considéré comme la base de toute l'informatique :
excusez du peu !
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() est un groupe commutatif.
est un groupe commutatif.
![]() ,
, ![]() et
et ![]() éléments de
éléments de ![]() ,
,
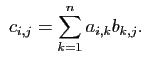
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales