Puissances d'une matrice.
Si deux matrices  et
et 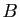 représentent le même
endomorphisme dans deux bases différentes, alors il en est de même
de
représentent le même
endomorphisme dans deux bases différentes, alors il en est de même
de 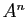 et
et 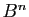 , pour tout
, pour tout
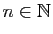 , et également de
, et également de 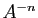 et
et
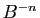 si cet endomorphisme est inversible.
si cet endomorphisme est inversible.
La puissance 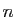 -ième d'une matrice diagonale s'écrit
immédiatement. Pour un bloc de Jordan, ce n'est pas beaucoup plus
compliqué.
Nous vous laissons vérifier que pour
-ième d'une matrice diagonale s'écrit
immédiatement. Pour un bloc de Jordan, ce n'est pas beaucoup plus
compliqué.
Nous vous laissons vérifier que pour
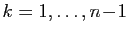 ,
, 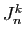 est la
matrice dont les termes de la forme
est la
matrice dont les termes de la forme 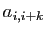 sont égaux à
sont égaux à  ,
les autres étant nuls. Pour
,
les autres étant nuls. Pour
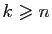 ,
, 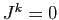 . Par la formule
du binôme de Newton, on en déduit l'expression
de
. Par la formule
du binôme de Newton, on en déduit l'expression
de
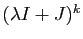 . On peut donc écrire explicitement la
puissance
. On peut donc écrire explicitement la
puissance 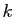 -ième d'une réduction de Jordan.
Cependant, nous ne vous conseillons pas cette
méthode, car il est plus facile d'utiliser le théorème de
Cayley-Hamilton :
-ième d'une réduction de Jordan.
Cependant, nous ne vous conseillons pas cette
méthode, car il est plus facile d'utiliser le théorème de
Cayley-Hamilton : 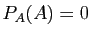 . Reprenons notre premier exemple, une
matrice
. Reprenons notre premier exemple, une
matrice  dont les 3 valeurs propres sont
dont les 3 valeurs propres sont 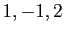 . Le polynôme
caractéristique est
. Le polynôme
caractéristique est
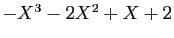 . Vous en déduisez donc que
. Vous en déduisez donc que
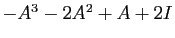 est la matrice nulle. Non seulement
est la matrice nulle. Non seulement 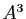 , mais
toutes les puissances de
, mais
toutes les puissances de  sont des combinaisons linéaires des
trois matrices
sont des combinaisons linéaires des
trois matrices 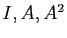 . En effet :
. En effet :
Ainsi vous pouvez calculer de proche en proche toutes les puissances
positives de  . Mais aussi :
. Mais aussi :
donc toutes les puissances négatives de  sont aussi des combinaisons
linéaires de
sont aussi des combinaisons
linéaires de 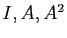 .
Algorithme de calcul du polynôme minimal.
.
Algorithme de calcul du polynôme minimal.
Il y a deux manières de voir un polynôme annulateur : comme un
polynôme de matrices qui s'annule pour 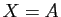 ,
ou bien comme une combinaison linéaire nulle des puissances de
,
ou bien comme une combinaison linéaire nulle des puissances de
 : le théorème de Cayley-Hamilton affirme que
la famille des
: le théorème de Cayley-Hamilton affirme que
la famille des 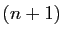 matrices
matrices
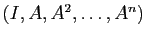 , considérée comme famille
dans un espace vectoriel de dimension
, considérée comme famille
dans un espace vectoriel de dimension 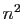 , est une famille liée.
Ceci est la base de l'algorithme de calcul du polynôme minimal par
la méthode du pivot de Gauss,
qui est utilisé dans les logiciels. Toute
combinaison linéaire nulle et non triviale
des matrices
, est une famille liée.
Ceci est la base de l'algorithme de calcul du polynôme minimal par
la méthode du pivot de Gauss,
qui est utilisé dans les logiciels. Toute
combinaison linéaire nulle et non triviale
des matrices
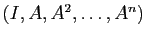 correpond à un
polynôme annulateur de
correpond à un
polynôme annulateur de  .
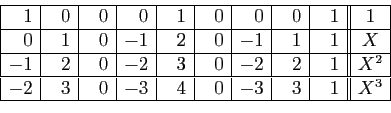
Si nous effectuons cette recherche avec des puissances de
.
Si nous effectuons cette recherche avec des puissances de  les
plus petites possibles, comme il existe un et un seul polynôme annulateur
unitaire de degré minimal (proposition 4),
nous en déduisons un moyen systématique pour trouver le polynôme minimal
de
les
plus petites possibles, comme il existe un et un seul polynôme annulateur
unitaire de degré minimal (proposition 4),
nous en déduisons un moyen systématique pour trouver le polynôme minimal
de  . Une manière naturelle de procéder est de considérer les matrices
. Une manière naturelle de procéder est de considérer les matrices
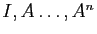 comme vecteurs de
comme vecteurs de
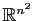 , de les
disposer en ordre croissant des puissances et d'effectuer la mise
sous forme échelonnée de ces
, de les
disposer en ordre croissant des puissances et d'effectuer la mise
sous forme échelonnée de ces 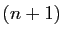 vecteurs, en s'interdisant de
permuter des lignes, en ne s'autorisant que des permutations de colonnes
pour pouvoir avancer dans la recherche de pivots non nuls par la méthode
de Gauss. Quand la mise sous forme échelonnée est faite, la première
ligne qui ne présente que des 0, (à un coefficient scalaire multiplicatif
près) contient la combinaison linéaire des vecteurs de départ faisant
intervenir les plus basses puissances possibles de
vecteurs, en s'interdisant de
permuter des lignes, en ne s'autorisant que des permutations de colonnes
pour pouvoir avancer dans la recherche de pivots non nuls par la méthode
de Gauss. Quand la mise sous forme échelonnée est faite, la première
ligne qui ne présente que des 0, (à un coefficient scalaire multiplicatif
près) contient la combinaison linéaire des vecteurs de départ faisant
intervenir les plus basses puissances possibles de  . Elle contient
donc le polynôme minimal. Pour mémoriser les opérations effectuées
pendant la mise sous forme échelonnée par la méthode de Gauss, ajoutons
une dernière colonne contenant
. Elle contient
donc le polynôme minimal. Pour mémoriser les opérations effectuées
pendant la mise sous forme échelonnée par la méthode de Gauss, ajoutons
une dernière colonne contenant
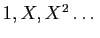 et effectuons aussi
sur cette colonne les opérations élémentaires de la méthode de Gauss.
Nous aurons alors dans cette colonne pour la première ligne ne contenant
que des 0, à un coefficient multiplicatif près, l'expression du
polynôme minimal de
et effectuons aussi
sur cette colonne les opérations élémentaires de la méthode de Gauss.
Nous aurons alors dans cette colonne pour la première ligne ne contenant
que des 0, à un coefficient multiplicatif près, l'expression du
polynôme minimal de  , non factorisé.
Voici un exemple. Soit
, non factorisé.
Voici un exemple. Soit
Formons le premier tableau de la méthode. Pour 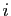 allant de 0 à
allant de 0 à
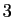 , on trouve sur la ligne
, on trouve sur la ligne 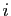 les 9 coefficients de la matrice
les 9 coefficients de la matrice 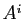 , suivis de
, suivis de 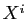 .
.
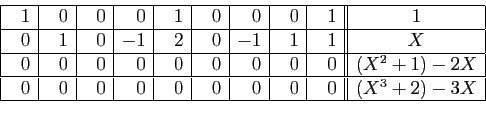
Dans le second tableau, des combinaisons linéaires de lignes annulent
les coefficients de la première colonne après le premier.
Dans le troisième tableau, on annule les coefficients de la seconde
colonne, après les 2 premiers.
Donc
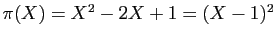 est le polynôme minimal de
est le polynôme minimal de
 . Nous obtenons aussi que
. Nous obtenons aussi que
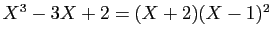 est annulateur,
ce qui n'est pas très utile : le facteur
est annulateur,
ce qui n'est pas très utile : le facteur 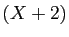 est parasite et nous ne cherchons pas à utiliser l'information
(sans intérêt pour nous) associée. Au vu du polynôme minimal,
nous voyons que
est parasite et nous ne cherchons pas à utiliser l'information
(sans intérêt pour nous) associée. Au vu du polynôme minimal,
nous voyons que
 admet
admet  comme seule valeur propre et la réduction de Jordan de
comme seule valeur propre et la réduction de Jordan de  fera intervenir un bloc
fera intervenir un bloc 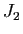 et un bloc
et un bloc 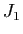 . La mise sous
forme de Jordan est particulièrement simple ici
parce que
. La mise sous
forme de Jordan est particulièrement simple ici
parce que
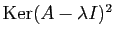 pour
pour 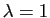 est
est
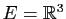 tout entier. Prenons donc
un vecteur dans
tout entier. Prenons donc
un vecteur dans 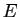 , «au hasard»
, «au hasard» 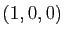 , formons
, formons
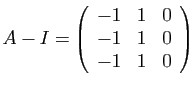 d'où
d'où
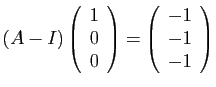 et
et
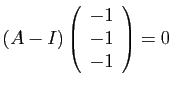 . Donc
. Donc
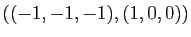 peut être choisi pour constituer
la base associée au bloc de longueur
peut être choisi pour constituer
la base associée au bloc de longueur 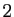 . En lui ajoutant le vecteur
. En lui ajoutant le vecteur
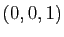 , vecteur propre évident, non colinéaire à
, vecteur propre évident, non colinéaire à
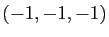 ,
nous savons que dans la base
,
nous savons que dans la base
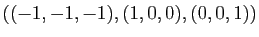 l'endomorphisme associé à
l'endomorphisme associé à  dans la base canonique de
dans la base canonique de
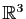 sera représenté par
sera représenté par
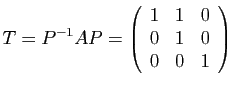
où
Systèmes différentiels linéaires.
La réduction des endomorphismes est très utilisée dans la
résolution des systèmes linéaires d'équations différentielles :
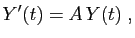 |
(E) |
où 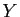 est une fonction (inconnue) de
est une fonction (inconnue) de
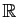 dans
dans
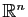 ,
,
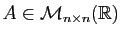 est une matrice de réels, carrée de taille
est une matrice de réels, carrée de taille
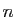 . Nous allons voir comment, d'abord d'un point de vue théorique.
Dans le cas particulier
. Nous allons voir comment, d'abord d'un point de vue théorique.
Dans le cas particulier 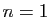 , la matrice est réduite à un scalaire
, la matrice est réduite à un scalaire 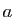 ,
et la solution de
,
et la solution de
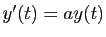 , partant de
, partant de 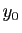 à l'instant 0 est :
à l'instant 0 est :
On peut définir
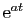 comme la somme de la série entière, de
rayon de convergence infini,
comme la somme de la série entière, de
rayon de convergence infini,
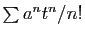 . Sa dérivée est :
. Sa dérivée est :
Cette écriture formelle reste valable en dimension 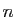 .
Pour trouver une solution à l'équation (E), il suffit
d'écrire de manière analogue
.
Pour trouver une solution à l'équation (E), il suffit
d'écrire de manière analogue
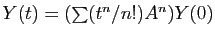 . Encore
faut-il
s'assurer que cette série entière, à coefficients matriciels,
converge, ce que nous admettrons.
. Encore
faut-il
s'assurer que cette série entière, à coefficients matriciels,
converge, ce que nous admettrons.
L'exponentielle de matrice a des propriétés comparables à l'exponentielle
ordinaire. En particulier :
Proposition 12
Si deux matrices 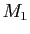 et
et 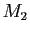 commutent, alors :
commutent, alors :
La propriété qui nous intéresse est la suivante :
Proposition 13
Soit
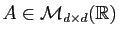 . Alors :
. Alors :
Il s'ensuit immédiatement que
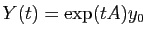 est solution de
(E), pour
est solution de
(E), pour 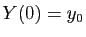 .
Le résultat suivant relie les
coefficients de
.
Le résultat suivant relie les
coefficients de 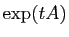 aux valeurs propres de la matrice
aux valeurs propres de la matrice  .
.
Démonstration : Nous utiliserons la réduction de Jordan de la matrice  :
:
La matrice 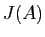 est une matrice diagonale par blocs.
À chaque valeur propre
est une matrice diagonale par blocs.
À chaque valeur propre
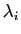 de
de  est associé un bloc
est associé un bloc 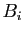 , qui est
la somme de
, qui est
la somme de
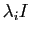 et d'un bloc
nilpotent
et d'un bloc
nilpotent 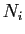 dont la puissance
dont la puissance 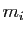 -ième est nulle.
Sur la définition de l'exponentielle, il est facile de vérifier que :
-ième est nulle.
Sur la définition de l'exponentielle, il est facile de vérifier que :
De plus si 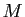 est diagonale par blocs, alors
est diagonale par blocs, alors 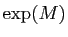 l'est aussi et ses
blocs sont les exponentielles des blocs de
l'est aussi et ses
blocs sont les exponentielles des blocs de 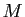 . Ces observations montrent
que les coefficients de
. Ces observations montrent
que les coefficients de 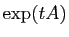 sont des combinaisons linéaires des
coefficients des
sont des combinaisons linéaires des
coefficients des
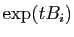 . Or :
. Or :
La matrice 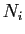 est constituée de blocs de Jordan
est constituée de blocs de Jordan 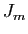 de dimension
de dimension
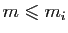 .
On obtient :
.
On obtient :
d'où le résultat. Exemple 1.
Exemple 1.
Considérons la matrice  suivante :
suivante :
Sa forme de Jordan est :
L'exponentielle de 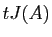 est :
est :
Si
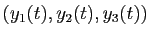 est solution du système
ci-dessous,
les fonctions
est solution du système
ci-dessous,
les fonctions 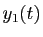 ,
, 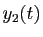 ,
, 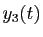 sont
nécessairement des combinaisons
linéaires de
sont
nécessairement des combinaisons
linéaires de
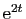 ,
,
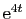 et
et
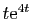 .
.
Par exemple la solution du système pour
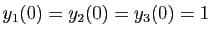 est :
est :
Après avoir résolu un système différentiel linéaire à coefficient
constants avec une démarche théorique utilisant l'exponentielle de
la matrice du système, voyons comment dans la pratique on effectue
cette recherche, et refaisons le chemin sur des exemples. (Les répétitions
avec ce qui précède sont volontaires).
Exemple 2.
Nous voulons résoudre le système différentiel (réel)
où
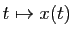 et
et
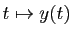 sont deux fonctions inconnues de
sont deux fonctions inconnues de
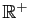 dans
dans
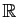 et cela connaissant
et cela connaissant
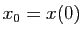 et
et
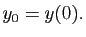 Posons
Posons
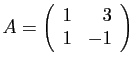 et cherchons à diagonaliser
et cherchons à diagonaliser  .
Calculons donc son polynôme caractéristique
.
Calculons donc son polynôme caractéristique
Comme ce polynôme caractéristique admet deux racines distinctes (de
multiplicité  ), nous savons que nous pourrons diagonaliser
), nous savons que nous pourrons diagonaliser  .
.
Recherchons le sous espace propre associé à
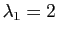 . Il faut
résoudre
. Il faut
résoudre
d'où 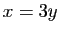 et donc
et donc
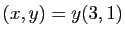 et donc
et donc
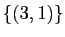 est une base de
est une base de
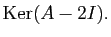
Recherchons le sous espace propre associé à
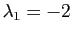 . Il
faut résoudre
. Il
faut résoudre
d'où 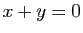 et donc
et donc
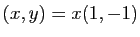 et donc
et donc
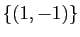 est une base de
est une base de
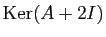 .
.
Posons
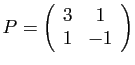 , alors
, alors
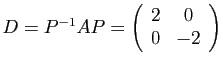 .
En termes de système différentiel :
.
En termes de système différentiel :
Posons donc
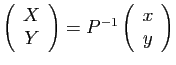 :
:
Ainsi la diagonalisation a découplé les nouvelles fonctions inconnues.
Il existe deux constantes réelles 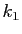 et
et 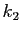 telles
que
telles
que
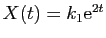 et
et
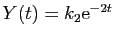 . En revenant à la
définition de
. En revenant à la
définition de 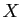 et de
et de 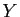
Pour 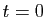 il reste
il reste
et donc
La solution du système est
Ou encore :
La matrice
vérifie
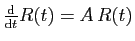 et
et 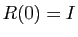 . C'est l'exponentielle de
. C'est l'exponentielle de
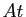 . On la nomme résolvante
du problème de Cauchy consistant à trouver la solution du
système connaissant sa valeur en
. On la nomme résolvante
du problème de Cauchy consistant à trouver la solution du
système connaissant sa valeur en 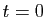 .
Cette solution du système est donnée explicitement en fonction
des conditions initiales
.
Cette solution du système est donnée explicitement en fonction
des conditions initiales 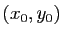 . Au passage, nous avons obtenu
une solution définie sur
. Au passage, nous avons obtenu
une solution définie sur
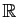 tout entier,
et nous pourrions démontrer
ainsi l'existence et l'unicité de la solution au problème de
Cauchy.
Cela ne survient que parce que
le système est linéaire à coefficients constants (sinon le domaine
de définition de la solution n'est pas
tout entier,
et nous pourrions démontrer
ainsi l'existence et l'unicité de la solution au problème de
Cauchy.
Cela ne survient que parce que
le système est linéaire à coefficients constants (sinon le domaine
de définition de la solution n'est pas
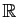 , a priori). Noter
que les coefficients constants interviennent de manière cruciale dans
, a priori). Noter
que les coefficients constants interviennent de manière cruciale dans
Si les coefficients de la matrice  ne sont pas constants n'utilisez
pas la diagonalisation !
Exemple 3.
ne sont pas constants n'utilisez
pas la diagonalisation !
Exemple 3.
Considérons le système
où
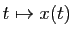 et
et
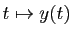 sont deux fonctions inconnues de
sont deux fonctions inconnues de
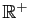 dans
dans
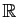 et cela connaissant
et cela connaissant
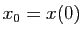 et
et
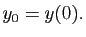 Posons
Posons
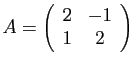 et cherchons à diagonaliser
et cherchons à diagonaliser  . Calculons donc son polynôme caractéristique
. Calculons donc son polynôme caractéristique
Comme le polynôme caractéristique n'admet pas de racines dans
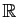 ,
la méthode précédente semble tomber à l'eau.
,
la méthode précédente semble tomber à l'eau.
Nous pourrions décider de passer dans
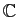 .
Pour cela factorisons
.
Pour cela factorisons
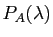 comme polynôme à coefficients
complexes.
comme polynôme à coefficients
complexes.
et nous obtenons deux racines complexes
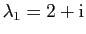 et
et
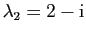 de multiplicité
de multiplicité  . Nous pourrions donc diagonaliser comme dans
l'exemple de la rotation en passant dans
. Nous pourrions donc diagonaliser comme dans
l'exemple de la rotation en passant dans
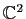 . Qu'obtiendrait-on
? Une fois tous les calculs faits nous aurions
. Qu'obtiendrait-on
? Une fois tous les calculs faits nous aurions
où  ,
,  ,
,  et
et 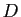 sont des constantes complexes reliées par deux
relations.
sont des constantes complexes reliées par deux
relations.
Comme nous manquons de courage pour ces calculs, nous allons procéder
à l'envers, en faisant la remarque suivante : oui il y a bien un moyen
de soutirer de la résolution complexe la résolution réelle, en regroupant
de manière astucieuse les vecteurs propres complexes associés à une
valeur propre complexe et à sa conjuguée
(comme le polynôme caractéristique
est à coefficients réels, si un complexe est racine, alors son complexe
conjugué aussi). Cela aura comme conséquence de choisir A et B de
sorte que 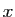 devienne réel et aussi
devienne réel et aussi 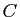 et
et 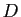 de sorte que
de sorte que 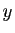 deviennent réel. Autrement dit la solution réelle sera de la forme
deviennent réel. Autrement dit la solution réelle sera de la forme
où 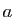 ,
, 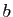 ,
, 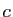 et
et 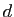 sont des constantes réelles
reliées par deux relations.
(Attention
sont des constantes réelles
reliées par deux relations.
(Attention 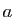 n'est pas la partie réelle de
n'est pas la partie réelle de  ...)
Concrètement
il y a deux racines complexes
...)
Concrètement
il y a deux racines complexes
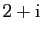 et
et
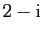 , il faut séparer la
partie réelle donnant
, il faut séparer la
partie réelle donnant
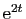 et la partie imaginaire pure donnant
et la partie imaginaire pure donnant
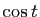 et
et 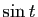 ). Mais je n'ai toujours pas les relations en
question puisque je n'ai pas fait les calculs, direz vous ! Oui,
mais puisque nous savons que la solution sera de cette forme, pourquoi
ne pas faire les calculs à l'envers et reporter la forme ci-dessus
dans le système de départ ? Ainsi, nous aurons les relations recherchées,
et nous n'aurons pas besoin d'effectuer la diagonalisation complexe !
De fait les calculs sont beaucoup plus rapides et simples, et conduisent
bien au résultat.
). Mais je n'ai toujours pas les relations en
question puisque je n'ai pas fait les calculs, direz vous ! Oui,
mais puisque nous savons que la solution sera de cette forme, pourquoi
ne pas faire les calculs à l'envers et reporter la forme ci-dessus
dans le système de départ ? Ainsi, nous aurons les relations recherchées,
et nous n'aurons pas besoin d'effectuer la diagonalisation complexe !
De fait les calculs sont beaucoup plus rapides et simples, et conduisent
bien au résultat.
Nous utilisons donc la diagonalisation complexe uniquement
pour connaître la forme de la solution, mais ce passage est crucial.
Si 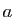 ,
, 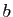 ,
, 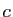 et
et 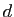 sont 4 constantes réelles, reportons donc la forme
indiquée dans le système initial brut.
sont 4 constantes réelles, reportons donc la forme
indiquée dans le système initial brut.
devrait
donner
et nous obtenons
ou encore 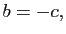
 donc
donc
et pour 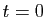 ,
,
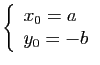 .
La solution du système est donc
.
La solution du système est donc
ou encore mieux
La matrice
vérifie
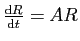 et
et 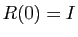 .
Elle est la résolvante
du problème de Cauchy posé initialement.
.
Elle est la résolvante
du problème de Cauchy posé initialement.
Comme vous l'avez constaté sur l'exemple ci dessus, la réduction à
la forme diagonale a été cruciale pour connaître la forme de
la solution
d'un système réel
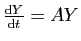 , où
, où  est une
matrice constante. Et si la matrice
est une
matrice constante. Et si la matrice  n'est pas diagonalisable ?
Comme nous disposons de la réduction de Jordan et que nous avons
compris théoriquement la démarche à effectuer nous avons (sans nous
en rendre compte) justifié la démarche pratique proposée souvent par
les physiciens.
Recette pratique.
n'est pas diagonalisable ?
Comme nous disposons de la réduction de Jordan et que nous avons
compris théoriquement la démarche à effectuer nous avons (sans nous
en rendre compte) justifié la démarche pratique proposée souvent par
les physiciens.
Recette pratique.
Soit à résoudre
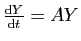 , où
, où
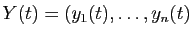 est un
est un 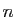 -uplet de fonctions
inconnues et
-uplet de fonctions
inconnues et  est une matrice constante.
est une matrice constante.
- Trouver les valeurs propres réelles ou complexes et leurs
multiplicités :
mettons
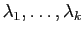 de multiplicités
de multiplicités
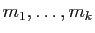 sont les racines du polynôme caractéristique
sont les racines du polynôme caractéristique
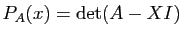 (avec
(avec
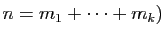 .
.
- Trouver les dimensions des sous espaces propres
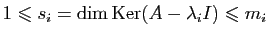 .
.
- Séparer les valeurs propres réelles des valeurs propres complexes.
- À une valeur propre réelle, mettons
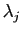 ,
on associe
,
on associe
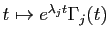 où
où
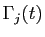 est un polynôme réel de degré
est un polynôme réel de degré
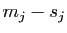 .
.
- Chaque valeur propre complexe doit être associée à
la valeur propre
complexe conjuguée (qui est aussi valeur propre puisque le polynôme
caractéristique est à coefficients réels). Disons
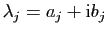 et
et
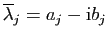 : à ce couple on associe
les fonctions
: à ce couple on associe
les fonctions
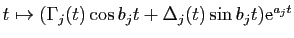 où
où
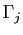 et
et
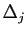 sont des polynômes réels de degré
sont des polynômes réels de degré
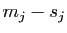 .
Ce faisant on introduit trop de constantes réelles !
.
Ce faisant on introduit trop de constantes réelles !
- On reporte dans le système initial la somme des fonctions
génériques
introduites dans 4) et 5), mais pour chaque fonction inconnue, on
introduit des constantes différentes. (Comme on ne possède pas la
matrice de passage de la base canonique
à une base qui réduit l'endomorphisme,
cela revient à prendre les coefficients de la matrice
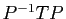 où
où 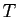 est la forme réduite de l'endomorphisme de manière quelconque,
en ne retenant que l'idée que chaque élément sera une combinaison
linéaire des fonctions génériques de 4) et 5) et donc chaque fonction
inconnue aussi). On en introduit donc beaucoup trop! On constate que
le nombre de constantes introduites est bien
est la forme réduite de l'endomorphisme de manière quelconque,
en ne retenant que l'idée que chaque élément sera une combinaison
linéaire des fonctions génériques de 4) et 5) et donc chaque fonction
inconnue aussi). On en introduit donc beaucoup trop! On constate que
le nombre de constantes introduites est bien 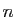 la dimension du
système, une fois toutes les équations du système
vérifiées. La recette
dit que cela marche sans expliquer pourquoi ! Il faut pour cela résoudre
les systèmes linéaires obtenus (en identifiant les coefficients des
fonctions génériques qui forment un système libre dans l'espace vectoriel
des fonctions réelles d'une variable réelle) et ramener le nombre
de constantes à
la dimension du
système, une fois toutes les équations du système
vérifiées. La recette
dit que cela marche sans expliquer pourquoi ! Il faut pour cela résoudre
les systèmes linéaires obtenus (en identifiant les coefficients des
fonctions génériques qui forment un système libre dans l'espace vectoriel
des fonctions réelles d'une variable réelle) et ramener le nombre
de constantes à 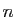 .
.
- On a obtenu la forme de la solution générale dépendant de
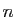 constantes
réelles, on y fait
constantes
réelles, on y fait 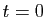 et on extrait l'expression de ces constantes
en fonction des conditions initiales (cela peut être redoutable si
et on extrait l'expression de ces constantes
en fonction des conditions initiales (cela peut être redoutable si
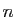 est grand, uniquement possible numériquement et/ou de manière
approchée !).
est grand, uniquement possible numériquement et/ou de manière
approchée !).
(fin de la recette)
Dans la recette précédente, rien n'est démontré, on affirme
simplement que cela marche, mais c'est une conséquence du théorème
8 comme expliqué au dessus ! En fait
la recette reste dans la base canonique de
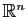 , introduit
beaucoup trop de constantes, puis en vérifiant le système
«à l'envers»,
calcule directement le produit
, introduit
beaucoup trop de constantes, puis en vérifiant le système
«à l'envers»,
calcule directement le produit 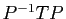 qui donne la solution générale,
et cela dans la base canonique de
qui donne la solution générale,
et cela dans la base canonique de
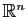 , sans avoir besoin
de calculer la matrice de passage
, sans avoir besoin
de calculer la matrice de passage 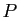 , ni
, ni 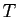 ni
ni 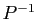 , ni
la solution générale dans la nouvelle base, ni le retour à l'ancienne
base ! C'est pour cela que la recette est rapide et efficace. Pour
la justifier il faut simplement démonter la formule
, ni
la solution générale dans la nouvelle base, ni le retour à l'ancienne
base ! C'est pour cela que la recette est rapide et efficace. Pour
la justifier il faut simplement démonter la formule
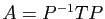 avec
avec 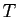 sous forme de Jordan (pensez à triangulaire supérieure avec
des coefficients non nuls uniquement sur la diagonale et sur la «diagonale
juste au dessus»), puis refaire le passage
réels
sous forme de Jordan (pensez à triangulaire supérieure avec
des coefficients non nuls uniquement sur la diagonale et sur la «diagonale
juste au dessus»), puis refaire le passage
réels
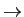 complexes
complexes
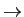 réels
comme expliqué dans l'exemple 3.
réels
comme expliqué dans l'exemple 3.
De plus on peut aussi sauter l'étape 2 et prendre les
polynômes
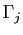 et
et
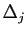 de degré
de degré
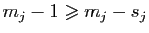 . On introduit
alors encore d'autres constantes inutiles. Les systèmes linéaires
obtenus, de taille plus grande, vont rendre nulles ces constantes
inutiles, ce qui embrouille souvent la compréhension de ce que l'on
fait. C'est souvent la méthode présentée par les physiciens. Cela
revient à utiliser
. On introduit
alors encore d'autres constantes inutiles. Les systèmes linéaires
obtenus, de taille plus grande, vont rendre nulles ces constantes
inutiles, ce qui embrouille souvent la compréhension de ce que l'on
fait. C'est souvent la méthode présentée par les physiciens. Cela
revient à utiliser 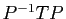 avec
avec 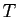 sous forme triangulaire supérieure,
sans essayer à savoir si
sous forme triangulaire supérieure,
sans essayer à savoir si 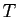 peut être mise sous une forme plus
intrinsèque,
décomposant
peut être mise sous une forme plus
intrinsèque,
décomposant
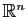 en sous espaces stables par
en sous espaces stables par  .
Comme le comportement du système différentiel, localement et globalement
est profondément lié à cette décomposition en sous espaces stables,
décortiquer le comportement du système différentiel demande de comprendre
la décomposition de Jordan. Cela revient à décomposer le système en
un certain nombre de sous-systèmes indépendants et analyser le comportement
de chacun des sous-systèmes possibles, ceux qui correspondent à la
découverte de Jordan.
Exemple 4.
.
Comme le comportement du système différentiel, localement et globalement
est profondément lié à cette décomposition en sous espaces stables,
décortiquer le comportement du système différentiel demande de comprendre
la décomposition de Jordan. Cela revient à décomposer le système en
un certain nombre de sous-systèmes indépendants et analyser le comportement
de chacun des sous-systèmes possibles, ceux qui correspondent à la
découverte de Jordan.
Exemple 4.
On veut résoudre le problème de Cauchy, consistant à trouver
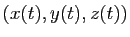 définies sur
définies sur
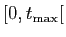 , telles que
, telles que
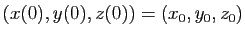 et
et
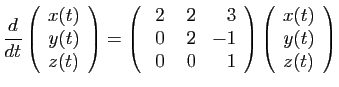
On pose
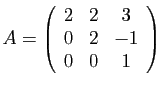
Le polynôme caractéristique est
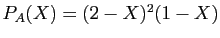 .
Recherchons donc les fonctions inconnues comme combinaisons linéaires
proposées par la recette
.
Recherchons donc les fonctions inconnues comme combinaisons linéaires
proposées par la recette
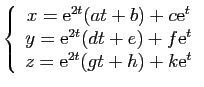
D'une part
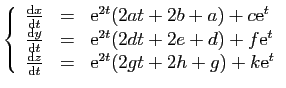
d'autre part
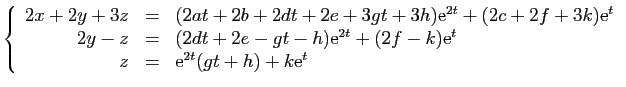
Nous avons donc un système linéaire de trois
équations. L'identification des coefficients de
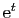 et
et
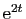 dans la troisième, puis la seconde, puis la première
équation
donne :
dans la troisième, puis la seconde, puis la première
équation
donne :
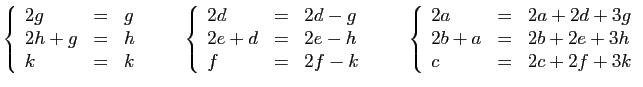
On en déduit 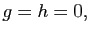 (ces constantes sont
nulles parce que le système initial
était triangulaire supérieur, pas parce que l'on avait sauté l'étape
deux, qui donnerait ici le même nombre de constantes) puis
(ces constantes sont
nulles parce que le système initial
était triangulaire supérieur, pas parce que l'on avait sauté l'étape
deux, qui donnerait ici le même nombre de constantes) puis 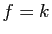 puis
puis 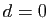 ,
, 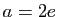 et
et 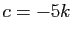 . Il vient :
. Il vient :
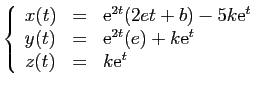
Pour 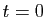 on obtient
on obtient
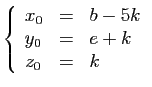
Finalement,
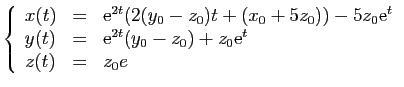
La solution est donc
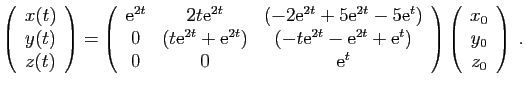
La matrice
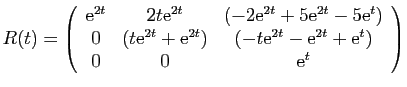
vérifie
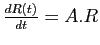 et
et
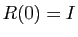 . C'est la résolvante du problème posé.
Difficile de faire plus rapide pour l'obtenir !
Équations aux différences.
. C'est la résolvante du problème posé.
Difficile de faire plus rapide pour l'obtenir !
Équations aux différences.
Pour terminer, nous allons démontrer deux résultats très
proches, portant l'un sur les équations de récurrence, l'autre sur
les équations différentielles. Vous connaissez déjà ces
résultats dans le cas 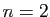 .
Soient
.
Soient
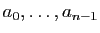
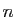 réels. Notons
réels. Notons 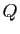 le polynôme
le polynôme
Notons
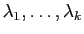 les racines de
les racines de 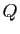 , et
, et
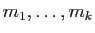 leurs multiplicités.
leurs multiplicités.
Théorème 9
Considérons l'équation :
Toute solution de
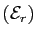 s'écrit :
s'écrit :
où les 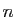 coefficients
coefficients
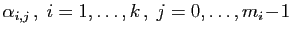 sont réels ou
complexes.
sont réels ou
complexes.
Théorème 10
Considérons
l'équation :
Toute solution de
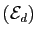 s'écrit :
s'écrit :
où les 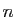 coefficients
coefficients
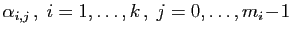 sont réels ou
complexes.
sont réels ou
complexes.
Démonstration : Les deux problèmes ont en commun leur écriture
matricielle. Posons pour tout
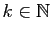
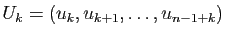
et
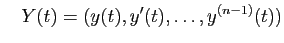
Les deux équations
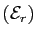 et
et
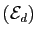 s'écrivent :
s'écrivent :
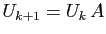
et
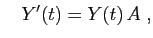
où  est la matrice compagnon du polynôme
est la matrice compagnon du polynôme 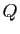 .
.
Les solutions sont :
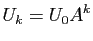
et
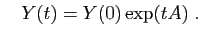
Nous avons déjà vu que le polynôme minimal et le polynôme
caractéristique de la matrice  sont tous les deux égaux à
sont tous les deux égaux à
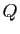 , au signe près. La réduction de Jordan de
, au signe près. La réduction de Jordan de  est de la forme
est de la forme
où 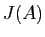 est une matrice diagonale par blocs.
À chaque valeur propre
est une matrice diagonale par blocs.
À chaque valeur propre
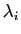 de
de  est associé un bloc
est associé un bloc 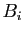 . Ce bloc a pour
taille la multiplicité
. Ce bloc a pour
taille la multiplicité 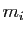 de
de 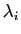 dans le polynôme
caractéristique. Il
est la somme de
dans le polynôme
caractéristique. Il
est la somme de
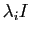 et d'un bloc
nilpotent
et d'un bloc
nilpotent 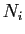 dont la puissance
dont la puissance 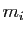 -ième est nulle.
-ième est nulle.
Pour le théorème 9,
Si une matrice 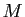 est diagonale par blocs, alors
est diagonale par blocs, alors 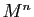 l'est aussi
et ses blocs sont les puissances
l'est aussi
et ses blocs sont les puissances 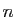 -ièmes des blocs de
-ièmes des blocs de 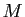 . Ces
observations montrent que les coefficients de
. Ces
observations montrent que les coefficients de 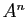 sont des combinaisons
linéaires des coefficients des
sont des combinaisons
linéaires des coefficients des 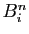 . Or les puissances successives
de
. Or les puissances successives
de 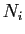 sont nulles à partir de la
sont nulles à partir de la 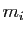 -ième. On a :
-ième. On a :
Tous les coefficients de 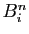 sont donc des combinaisons linéaires
de
sont donc des combinaisons linéaires
de
C'est donc aussi le cas pour les coefficients de 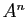 .
Pour
.
Pour 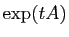 , le raisonnement
est celui de la démonstration du théorème 8.
, le raisonnement
est celui de la démonstration du théorème 8. 
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
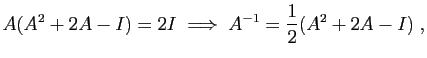
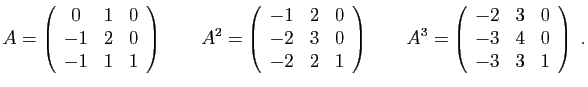

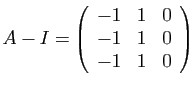 d'où
d'où
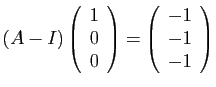 et
et
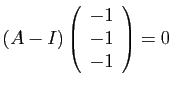 . Donc
. Donc
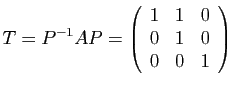 où
où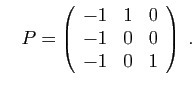
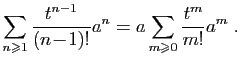
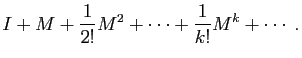
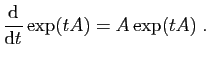

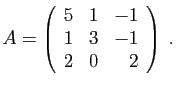
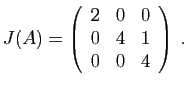
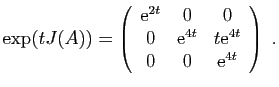
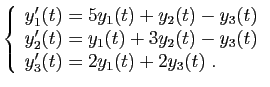
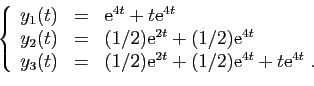
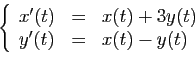
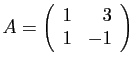 et cherchons à diagonaliser
et cherchons à diagonaliser 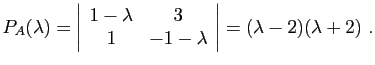
![]() . Il faut
résoudre
. Il faut
résoudre
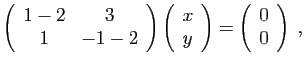
![]() . Il
faut résoudre
. Il
faut résoudre
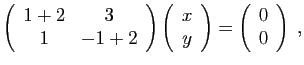
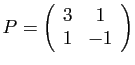 , alors
, alors
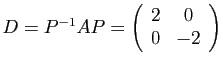 .
En termes de système différentiel :
.
En termes de système différentiel :
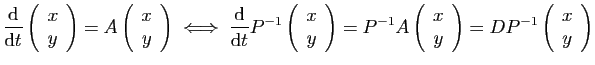
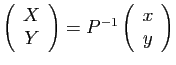 :
:
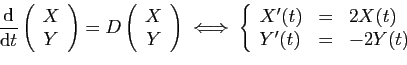
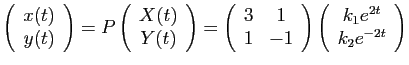
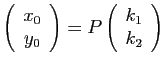
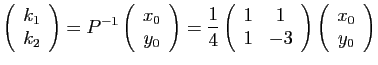
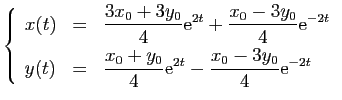
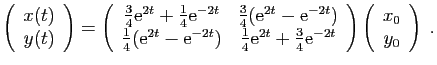
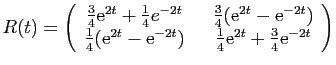
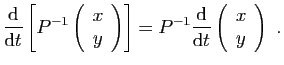
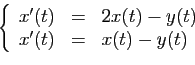
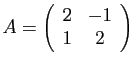 et cherchons à diagonaliser
et cherchons à diagonaliser 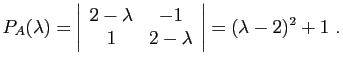
![]() ,
la méthode précédente semble tomber à l'eau.
,
la méthode précédente semble tomber à l'eau.
![]() .
Pour cela factorisons
.
Pour cela factorisons
![]() comme polynôme à coefficients
complexes.
comme polynôme à coefficients
complexes. 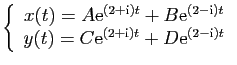
![]() devienne réel et aussi
devienne réel et aussi ![]() et
et ![]() de sorte que
de sorte que ![]() deviennent réel. Autrement dit la solution réelle sera de la forme
deviennent réel. Autrement dit la solution réelle sera de la forme
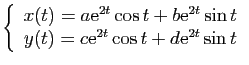
![]() ,
, ![]() ,
, ![]() et
et ![]() sont 4 constantes réelles, reportons donc la forme
indiquée dans le système initial brut.
sont 4 constantes réelles, reportons donc la forme
indiquée dans le système initial brut.
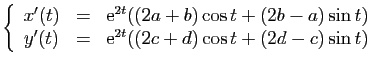
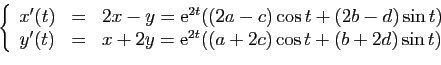
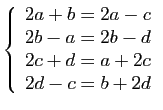
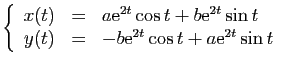
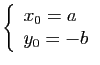 .
La solution du système est donc
.
La solution du système est donc
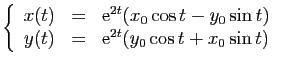
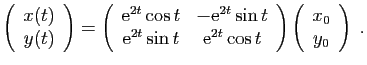
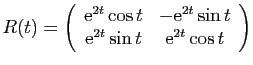
![]() , où
, où ![]() est une
matrice constante. Et si la matrice
est une
matrice constante. Et si la matrice ![]() n'est pas diagonalisable ?
Comme nous disposons de la réduction de Jordan et que nous avons
compris théoriquement la démarche à effectuer nous avons (sans nous
en rendre compte) justifié la démarche pratique proposée souvent par
les physiciens.
Recette pratique.
n'est pas diagonalisable ?
Comme nous disposons de la réduction de Jordan et que nous avons
compris théoriquement la démarche à effectuer nous avons (sans nous
en rendre compte) justifié la démarche pratique proposée souvent par
les physiciens.
Recette pratique.
![]() , où
, où
![]() est un
est un ![]() -uplet de fonctions
inconnues et
-uplet de fonctions
inconnues et ![]() est une matrice constante.
est une matrice constante.
![]() , introduit
beaucoup trop de constantes, puis en vérifiant le système
«à l'envers»,
calcule directement le produit
, introduit
beaucoup trop de constantes, puis en vérifiant le système
«à l'envers»,
calcule directement le produit ![]() qui donne la solution générale,
et cela dans la base canonique de
qui donne la solution générale,
et cela dans la base canonique de
![]() , sans avoir besoin
de calculer la matrice de passage
, sans avoir besoin
de calculer la matrice de passage ![]() , ni
, ni ![]() ni
ni ![]() , ni
la solution générale dans la nouvelle base, ni le retour à l'ancienne
base ! C'est pour cela que la recette est rapide et efficace. Pour
la justifier il faut simplement démonter la formule
, ni
la solution générale dans la nouvelle base, ni le retour à l'ancienne
base ! C'est pour cela que la recette est rapide et efficace. Pour
la justifier il faut simplement démonter la formule
![]() avec
avec ![]() sous forme de Jordan (pensez à triangulaire supérieure avec
des coefficients non nuls uniquement sur la diagonale et sur la «diagonale
juste au dessus»), puis refaire le passage
réels
sous forme de Jordan (pensez à triangulaire supérieure avec
des coefficients non nuls uniquement sur la diagonale et sur la «diagonale
juste au dessus»), puis refaire le passage
réels
![]() complexes
complexes
![]() réels
comme expliqué dans l'exemple 3.
réels
comme expliqué dans l'exemple 3.
![]() et
et
![]() de degré
de degré
![]() . On introduit
alors encore d'autres constantes inutiles. Les systèmes linéaires
obtenus, de taille plus grande, vont rendre nulles ces constantes
inutiles, ce qui embrouille souvent la compréhension de ce que l'on
fait. C'est souvent la méthode présentée par les physiciens. Cela
revient à utiliser
. On introduit
alors encore d'autres constantes inutiles. Les systèmes linéaires
obtenus, de taille plus grande, vont rendre nulles ces constantes
inutiles, ce qui embrouille souvent la compréhension de ce que l'on
fait. C'est souvent la méthode présentée par les physiciens. Cela
revient à utiliser ![]() avec
avec ![]() sous forme triangulaire supérieure,
sans essayer à savoir si
sous forme triangulaire supérieure,
sans essayer à savoir si ![]() peut être mise sous une forme plus
intrinsèque,
décomposant
peut être mise sous une forme plus
intrinsèque,
décomposant
![]() en sous espaces stables par
en sous espaces stables par ![]() .
Comme le comportement du système différentiel, localement et globalement
est profondément lié à cette décomposition en sous espaces stables,
décortiquer le comportement du système différentiel demande de comprendre
la décomposition de Jordan. Cela revient à décomposer le système en
un certain nombre de sous-systèmes indépendants et analyser le comportement
de chacun des sous-systèmes possibles, ceux qui correspondent à la
découverte de Jordan.
Exemple 4.
.
Comme le comportement du système différentiel, localement et globalement
est profondément lié à cette décomposition en sous espaces stables,
décortiquer le comportement du système différentiel demande de comprendre
la décomposition de Jordan. Cela revient à décomposer le système en
un certain nombre de sous-systèmes indépendants et analyser le comportement
de chacun des sous-systèmes possibles, ceux qui correspondent à la
découverte de Jordan.
Exemple 4.
![]() définies sur
définies sur
![]() , telles que
, telles que
![]() et
et
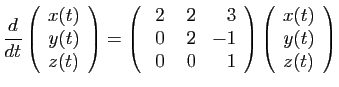
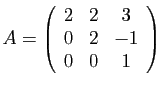
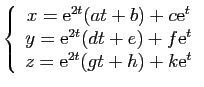
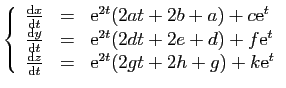
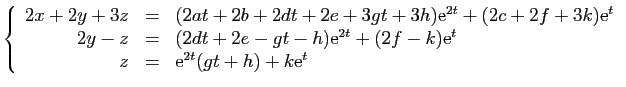
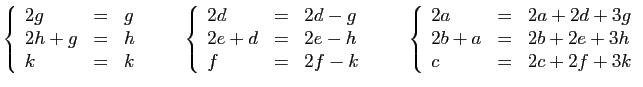
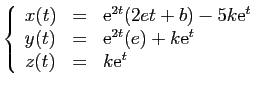
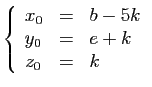
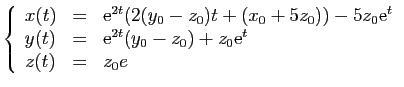
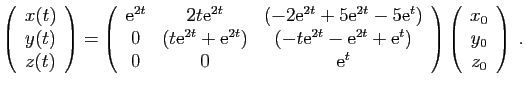
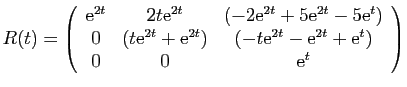
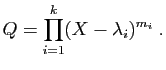
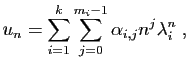
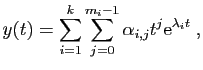

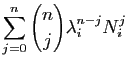
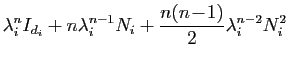
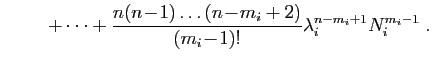
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales