- Un nombre complexe
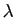 est une valeur propre de
est une valeur propre de 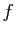 s'il existe un vecteur
s'il existe un vecteur 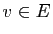 non nul, tel que
non nul, tel que
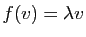 .
.
- Un vecteur
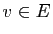 est un vecteur propre de
est un vecteur propre de 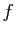 associé à
la valeur propre
associé à
la valeur propre 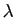 de
de 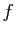 si
si 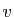 est non nul et
est non nul et
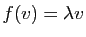 .
.
- Le sous-espace propre associé à la valeur propre
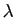 est l'ensemble des vecteurs
est l'ensemble des vecteurs 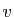 tels que
tels que
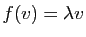 , à savoir
le noyau de l'endomorphisme
, à savoir
le noyau de l'endomorphisme
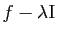 , où
, où
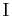 désigne
l'identité de
désigne
l'identité de 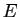 .
.
- On dit que
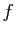 est diagonalisable s'il existe une base de
est diagonalisable s'il existe une base de 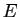 formée
de vecteurs propres pour
formée
de vecteurs propres pour 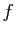 , ou encore si
, ou encore si 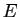 est la somme directe
des sous-espaces propres de
est la somme directe
des sous-espaces propres de 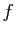 :
:
- On appelle polynôme caractéristique de
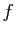 le polynôme
dont les racines sont les valeurs propres de
le polynôme
dont les racines sont les valeurs propres de
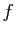 .
.
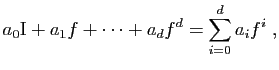
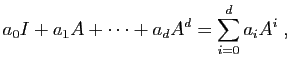
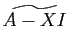
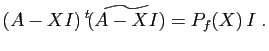
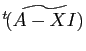
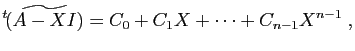
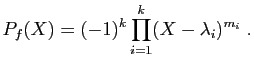
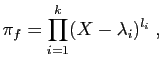
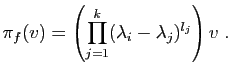
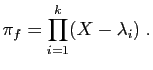
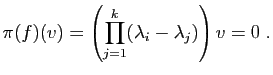
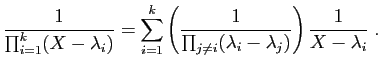
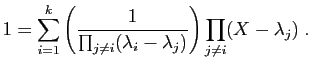
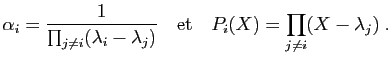
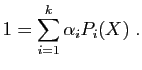
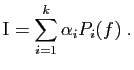
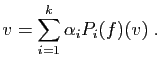
![\includegraphics[width=10cm]{projsym}](img272.gif)
 et
et

 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales