La procédure est un peu longue à appliquer, mais assez simple.
- Factoriser le polynôme caractéristique
Attention au calcul du déterminant : le but
étant de factoriser, vous avez intérêt à combiner des lignes ou
des colonnes, plutôt que de développer, même en
dimension 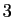 . Si le polynôme caractéristique a des racines
complexes, la matrice n'est pas diagonalisable dans
. Si le polynôme caractéristique a des racines
complexes, la matrice n'est pas diagonalisable dans
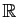 , mais elle
peut l'être dans
, mais elle
peut l'être dans
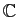 . Nous supposons désormais que le polynôme
caractéristique est scindé :
. Nous supposons désormais que le polynôme
caractéristique est scindé :
- Trouver une base de chaque sous-espace propre
Vous avez 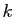 systèmes linéaires à résoudre.
Si pour l'une des valeurs propres
systèmes linéaires à résoudre.
Si pour l'une des valeurs propres 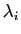 ,
le système
,
le système
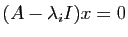 est de rang
strictement supérieur à
est de rang
strictement supérieur à 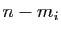 (l'ensemble des solutions est de
dimension strictement inférieure à
(l'ensemble des solutions est de
dimension strictement inférieure à 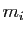 ), alors la matrice
n'est pas diagonalisable. Supposons que
vous ayez bien trouvé une base de
), alors la matrice
n'est pas diagonalisable. Supposons que
vous ayez bien trouvé une base de 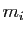 vecteurs propres pour
chaque valeur propre
vecteurs propres pour
chaque valeur propre 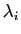 . Rassemblez les vecteurs que
vous avez trouvés pour chaque valeur propre, il y en a
. Rassemblez les vecteurs que
vous avez trouvés pour chaque valeur propre, il y en a 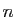 en tout.
La matrice dont les colonnes sont ces
en tout.
La matrice dont les colonnes sont ces 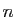 vecteurs est la
matrice de passage
vecteurs est la
matrice de passage 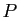 de la base canonique à la nouvelle base.
de la base canonique à la nouvelle base.
- Calculer l'inverse de
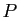
Vous avez alors explicité la diagonalisation :
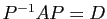 .
Attention à respecter le même ordre dans
l'écriture des valeurs propres, et dans celle des colonnes de
.
Attention à respecter le même ordre dans
l'écriture des valeurs propres, et dans celle des colonnes de 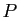 .
Le calcul de
.
Le calcul de 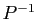 n'est pas indispensable, sauf si
vous avez explicitement besoin du changement de base.
n'est pas indispensable, sauf si
vous avez explicitement besoin du changement de base.
- Vérifiez vos calculs
Le plus simple est de calculer 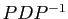 : vous devez retrouver
: vous devez retrouver
 . Vous pouvez aussi vérifier pour chacun des vecteurs que vous
avez trouvés qu'il est bien vecteur propre.
. Vous pouvez aussi vérifier pour chacun des vecteurs que vous
avez trouvés qu'il est bien vecteur propre.
Pour le cas des valeurs propres de multiplicité  ,
signalons comme alternative à la résolution du système
linéaire, la «méthode des cofacteurs», à utiliser
uniquement en dimensions
,
signalons comme alternative à la résolution du système
linéaire, la «méthode des cofacteurs», à utiliser
uniquement en dimensions 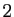 et
et 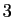 .
.
Proposition 2
Soit 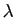 une valeur propre de
une valeur propre de  , de multiplicité
, de multiplicité
 . Considérons une ligne de
. Considérons une ligne de
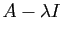 , choisie de façon que la
matrice formée des autres lignes de
, choisie de façon que la
matrice formée des autres lignes de
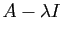 soit de rang
soit de rang 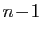 . Le vecteur
formé des cofacteurs associés à cette ligne
(les
. Le vecteur
formé des cofacteurs associés à cette ligne
(les 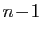 déterminants extraits en
barrant la ligne choisie et une colonne, avec alternance de signe)
est un vecteur propre de
déterminants extraits en
barrant la ligne choisie et une colonne, avec alternance de signe)
est un vecteur propre de  associé à
associé à 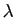 .
.
Démonstration : Si 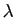 est de multiplicité
est de multiplicité  , alors le sous-espace propre
associé est de dimension
, alors le sous-espace propre
associé est de dimension  , et il suffit d'en trouver un
vecteur non nul. Soit
, et il suffit d'en trouver un
vecteur non nul. Soit
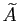 la comatrice de
la comatrice de  : c'est la
matrice des cofacteurs de
: c'est la
matrice des cofacteurs de  , à savoir les déterminants mineurs
d'ordre
, à savoir les déterminants mineurs
d'ordre 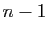 , extraits en supprimant une ligne et une colonne,
affectés de signes alternés. Il se trouve que
, extraits en supprimant une ligne et une colonne,
affectés de signes alternés. Il se trouve que
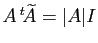 . Appliquons ce résultat à
. Appliquons ce résultat à
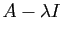 , qui est de
rang
, qui est de
rang 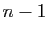 :
:
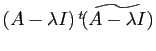 est la
matrice nulle. Cela signifie que les lignes de
est la
matrice nulle. Cela signifie que les lignes de
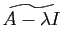 sont soit nulles, soit vecteur propre de
sont soit nulles, soit vecteur propre de  associé à
associé à 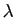 .
.  Nous détaillons d'abord l'exemple suivant, donné en introduction.
Nous détaillons d'abord l'exemple suivant, donné en introduction.
Commençons par écrire la matrice 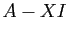 .
.
Il faut ensuite calculer son déterminant. Il serait maladroit
d'utiliser la règle de Sarrus pour développer le déterminant et
le factoriser ensuite. Il vaut mieux le factoriser en faisant
apparaître des zéros par combinaison de
lignes et de colonnes. Ajoutons d'abord la seconde colonne à la première :
On peut alors factoriser 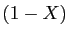 dans la première colonne :
dans la première colonne :
Soustrayons ensuite la première ligne à la seconde :
En développant selon la première colonne, il reste un
déterminant d'ordre 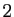 qui est facile à factoriser.
qui est facile à factoriser.
Les valeurs propres de  sont donc
sont donc  ,
, 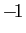 et
et 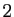 .
Comme elles sont distinctes, il suffit de trouver un vecteur propre
pour chacune.
Commençons par la valeur propre
.
Comme elles sont distinctes, il suffit de trouver un vecteur propre
pour chacune.
Commençons par la valeur propre  .
.
Observons que la matrice 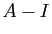 est bien de rang 2, comme prévu : la
somme des trois lignes est nulle et les deux premières
lignes sont indépendantes. Nous allons calculer les cofacteurs
associés à la troisième ligne. Ils valent (attention à
l'alternance de signe) :
est bien de rang 2, comme prévu : la
somme des trois lignes est nulle et les deux premières
lignes sont indépendantes. Nous allons calculer les cofacteurs
associés à la troisième ligne. Ils valent (attention à
l'alternance de signe) :
Tous les vecteurs non nuls, proportionnels au vecteur
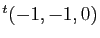 sont vecteurs propres de
sont vecteurs propres de  , associés à la valeur propre
, associés à la valeur propre  . Il
est conseillé de choisir le plus simple, ici :
. Il
est conseillé de choisir le plus simple, ici :
Le choix de la troisième ligne, pour calculer les cofacteurs, est
arbitraire. Il suffit que les deux lignes qui restent ne soient pas
proportionnelles (car tous les cofacteurs seraient nuls). Voici par
exemple les cofacteurs associés à la deuxième ligne.
On pourra trouver un vecteur différent, mais il sera
forcément proportionnel à
celui qu'on trouve avec une autre ligne. Cela ne change rien au choix
du vecteur propre.
Passons maintenant à la valeur propre 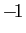 .
.
Les cofacteurs associés à la troisième ligne sont :
Ici encore, nous choisirons un vecteur plus simple, proportionnel
au vecteur des cofacteurs.
Voici le calcul pour la valeur propre 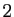 :
:
Les cofacteurs associés à la troisième ligne sont :
Nous choisirons un vecteur plus simple, proportionnel
au vecteur des cofacteurs.
La matrice de passage 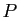 sera constituée en juxtaposant les
trois vecteurs
sera constituée en juxtaposant les
trois vecteurs
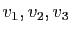 (en colonnes).
(en colonnes).
La matrice diagonale 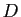 a pour coefficients diagonaux les trois
valeurs propres (attention : l'ordre des valeurs propres et des
vecteurs propres doit être le même).
a pour coefficients diagonaux les trois
valeurs propres (attention : l'ordre des valeurs propres et des
vecteurs propres doit être le même).
Nous n'insisterons pas sur le calcul de 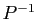 .
Observons que la diagonalisation trouvée est loin d'être
unique. On peut choisir un ordre différent pour les valeurs propres,
et pour chaque valeur propre, n'importe quel vecteur non nul
proportionnel à celui qui a été trouvé. On pourra vérifier
par exemple, pour la même matrice
.
Observons que la diagonalisation trouvée est loin d'être
unique. On peut choisir un ordre différent pour les valeurs propres,
et pour chaque valeur propre, n'importe quel vecteur non nul
proportionnel à celui qui a été trouvé. On pourra vérifier
par exemple, pour la même matrice  que les matrices
que les matrices 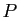 et
et 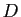 ci-dessous vérifient également
ci-dessous vérifient également
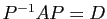 .
.
Dans l'exemple ci-dessous, la matrice  est symétrique. Pour le
choix des vecteurs propres, nous avons fait en sorte que
est symétrique. Pour le
choix des vecteurs propres, nous avons fait en sorte que
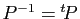 . La technique est la même.
Il faut simplement prendre garde
à choisir des vecteurs propres tels que
. La technique est la même.
Il faut simplement prendre garde
à choisir des vecteurs propres tels que 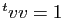 , ce qui
dispensera du calcul de
, ce qui
dispensera du calcul de 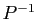 .
.
Voici un exemple en dimension 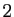 , où les valeurs propres sont des
nombres complexes (la matrice
, où les valeurs propres sont des
nombres complexes (la matrice  n'est donc pas diagonalisable dans
n'est donc pas diagonalisable dans
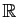 ). C'est la matrice de
la rotation vectorielle d'angle
). C'est la matrice de
la rotation vectorielle d'angle
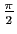 dans le plan.
dans le plan.
Voici maintenant un exemple où la valeur propre  est double. La
méthode des cofacteurs ne s'applique pas pour trouver les vecteurs
propres correspondants. Vous devez déterminer une base de
est double. La
méthode des cofacteurs ne s'applique pas pour trouver les vecteurs
propres correspondants. Vous devez déterminer une base de
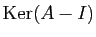 , en résolvant le système par la méthode du
pivot de Gauss comme vous avez appris à le faire. Ici la matrice
, en résolvant le système par la méthode du
pivot de Gauss comme vous avez appris à le faire. Ici la matrice
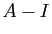 a une ligne nulle et deux lignes proportionnelles. Elle est donc
de rang
a une ligne nulle et deux lignes proportionnelles. Elle est donc
de rang  et le système se réduit à une seule équation,
et le système se réduit à une seule équation,
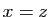 . Les deux vecteurs non proportionnels les plus simples solution
du système sont obtenus pour
. Les deux vecteurs non proportionnels les plus simples solution
du système sont obtenus pour
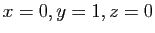 et
et
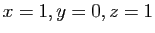 .
.
Vous vérifierez que les deux matrices suivantes, qui ont
une valeur propre double, ne
sont pas diagonalisables, car le sous-espace propre associé à la
valeur propre double est de dimension  et non pas
et non pas 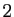 .
.
Que faire dans ce cas ? Les sections suivantes
répondent, entre autres, à cette question.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
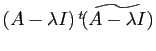
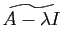
![\begin{displaymath}
\stackrel{
\underbrace{
\left(
\begin{array}{rrr}
\frac{1}{2...
...& 0 [2ex]
0&-1& 0 [2ex]
0&0& 2
\end{array}\right)
}}{D}
\end{displaymath}](img39.gif)
![\begin{displaymath}
A-X I=
\left(
\begin{array}{rrr}
-X&1&1 [2ex]
-\frac{1}{2}...
...2ex]
\frac{3}{2}&-\frac{3}{2}&\frac{1}{2}-X
\end{array}\right)
\end{displaymath}](img132.gif)
![\begin{displaymath}
P_A(X)=
\left\vert
\begin{array}{rrr}
-X&1&1 [2ex]
-\frac{...
...2} [2ex]
0&-\frac{3}{2}&\frac{1}{2}-X
\end{array}\right\vert
\end{displaymath}](img133.gif)
![\begin{displaymath}
P_A(X)
= (1\!-\!X)
\left\vert
\begin{array}{rrr}
1&1&1 [2e...
...2} [2ex]
0&-\frac{3}{2}&\frac{1}{2}-X
\end{array}\right\vert
\end{displaymath}](img135.gif)
![\begin{displaymath}
P_A(X)
= (1\!-\!X)
\left\vert
\begin{array}{rrr}
1&1&1 [2e...
...2} [2ex]
0&-\frac{3}{2}&\frac{1}{2}-X
\end{array}\right\vert
\end{displaymath}](img136.gif)
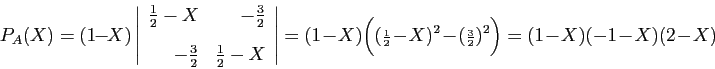
![\begin{displaymath}
A- I=
\left(
\begin{array}{rrr}
-1&1&1 [2ex]
-\frac{1}{2}&...
...[2ex]
\frac{3}{2}&-\frac{3}{2}&-\frac{1}{2}
\end{array}\right)
\end{displaymath}](img139.gif)
![\begin{displaymath}
A_{3,1} = +
\left\vert
\begin{array}{rr}
1&1 [2ex]
\frac{1...
... [2ex]
-\frac{1}{2}&\frac{1}{2}
\end{array}\right\vert = 0\;.
\end{displaymath}](img141.gif)
![\begin{displaymath}
v_1=
\left(
\begin{array}{r}
1 [2ex]
1 [2ex]
0
\end{array}\right)
\end{displaymath}](img143.gif)
![\begin{displaymath}
A_{2,1} = -
\left\vert
\begin{array}{rr}
1&1 [2ex]
-\frac{...
... [2ex]
\frac{3}{2}&-\frac{3}{2}
\end{array}\right\vert = 0\;.
\end{displaymath}](img144.gif)
![\begin{displaymath}
A-(-1) I=
\left(
\begin{array}{rrr}
1&1&1 [2ex]
-\frac{1}{...
... [2ex]
\frac{3}{2}&-\frac{3}{2}&\frac{3}{2}
\end{array}\right)
\end{displaymath}](img145.gif)
![\begin{displaymath}
A_{3,1} = +
\left\vert
\begin{array}{rr}
1&1 [2ex]
\frac{5...
... [2ex]
-\frac{1}{2}&\frac{5}{2}
\end{array}\right\vert = 3\;.
\end{displaymath}](img146.gif)
![\begin{displaymath}
v_2=
\left(
\begin{array}{r}
-1 [2ex]
0 [2ex]
1
\end{array}\right)
\end{displaymath}](img147.gif)
![\begin{displaymath}
A-2 I=
\left(
\begin{array}{rrr}
-2&1&1 [2ex]
-\frac{1}{2}...
...[2ex]
\frac{3}{2}&-\frac{3}{2}&-\frac{3}{2}
\end{array}\right)
\end{displaymath}](img148.gif)
![\begin{displaymath}
A_{3,1} = +
\left\vert
\begin{array}{rr}
1&1 [2ex]
-\frac{...
...c{1}{2}&-\frac{1}{2}
\end{array}\right\vert = {\frac{3}{2}}\;.
\end{displaymath}](img149.gif)
![\begin{displaymath}
v_3=
\left(
\begin{array}{r}
0 [2ex]
1 [2ex]
-1
\end{array}\right)
\end{displaymath}](img150.gif)
![\begin{displaymath}
P=
\left(
\begin{array}{rrr}
1&-1&0 [2ex]
1&0&1 [2ex]
0&1&-1
\end{array}\right)
\end{displaymath}](img152.gif)
![\begin{displaymath}
D=
\left(
\begin{array}{rrr}
1&0& 0 [2ex]
0&-1& 0 [2ex]
0&0& 2
\end{array}\right)
\end{displaymath}](img153.gif)
![\begin{displaymath}
P=
\left(
\begin{array}{rrr}
0&-1&3 [2ex]
2&-1&0 [2ex]
-...
...r}
2& 0&0 [2ex]
0& 1&0 [2ex]
0& 0&-1
\end{array}\right)
\end{displaymath}](img154.gif)
![\begin{displaymath}
\stackrel{
\underbrace{
\left(
\begin{array}{rrr}
\frac{1}{\...
...rr}
0&0&0 [2ex]
0&1&0 [2ex]
0&0&3
\end{array}\right)
}}{D}
\end{displaymath}](img155.gif)
![\begin{displaymath}
\stackrel{
\underbrace{
\left(
\begin{array}{rr}
\frac{1}{2}...
...r}
\mathrm{i}&0 [2ex]
0&-\mathrm{i}
\end{array}\right)
}}{D}
\end{displaymath}](img157.gif)
![\begin{displaymath}
\stackrel{
\underbrace{
\left(
\begin{array}{rrr}
0& 1&0 ...
... 0&0 [2ex]
0& 1&0 [2ex]
0& 0&-1
\end{array}\right)
}}{D}
\end{displaymath}](img162.gif)
![\begin{displaymath}
A=
\left(
\begin{array}{rr}
1&2 [2ex]
-2&-3
\end{array}\ri...
...}{rrr}
1&1&0 [2ex]
-1&0&-1 [2ex]
0&-1&1
\end{array}\right)
\end{displaymath}](img163.gif)
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales