Le théorème que nous allons vous exposer
n'est pas seulement splendide.
It is a testament to the fact that beautiful mathematics eventually
tend to be useful, and useful mathematics eventually tend to be
beautiful.
On en trouve en effet des applications, non seulement un peu partout
en mathématiques, mais aussi en économie, en théorie des
populations, dans les réseaux sociaux etc2. On peut
considérer par exemple que l'algorithme PageRank de Google en est un lointain
avatar. Ce théorème a été démontré
en 1907 par Oskar Perron (1880-1975).
La beauté du résultat tient d'une part à son élégance,
d'autre part dans un apparent paradoxe. La décomposition spectrale
d'une matrice est liée à
l'endomorphisme qu'elle représente, et elle est donc invariante
par changement de base. La conclusion du théorème
(existence d'une valeur propre
réelle supérieure au module de toute autre valeur propre) est liée
à l'endomorphisme et non à la matrice. Or l'hypothèse
(coefficients strictement positifs) n'est pas invariante par
changement de base. Pour comprendre ce paradoxe, il faut interpréter
l'hypothèse de façon géométrique. Par exemple en dimension 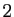 ,
considérez le quart de plan formé des vecteurs à coordonnées
strictement positives. Le fait que
,
considérez le quart de plan formé des vecteurs à coordonnées
strictement positives. Le fait que  soit à coefficients
strictement positifs entraîne que le produit par
soit à coefficients
strictement positifs entraîne que le produit par  d'un vecteur
à coordonnées strictement positives reste dans le même quart de
plan. En d'autres termes, l'endomorphisme laisse stable ce quart de
plan. Il n'est donc pas surprenant qu'il y ait dans ce même quart de
plan une direction invariante.
Soit dit entre parenthèses, Perron n'en était pas à un paradoxe près :
d'un vecteur
à coordonnées strictement positives reste dans le même quart de
plan. En d'autres termes, l'endomorphisme laisse stable ce quart de
plan. Il n'est donc pas surprenant qu'il y ait dans ce même quart de
plan une direction invariante.
Soit dit entre parenthèses, Perron n'en était pas à un paradoxe près :
Soit 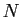 le plus grand entier naturel. Si
le plus grand entier naturel. Si 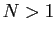 ,
alors
,
alors 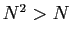 , ce qui contredit la définition. Donc
, ce qui contredit la définition. Donc 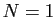 .
.
Démonstration : D'abord quelques notations pour faciliter la lecture. Pour tous vecteurs
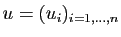 et
et
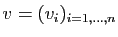 de
de
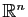 ,
,
-
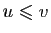 signifie
signifie
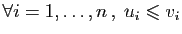 ,
,
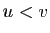 signifie
signifie
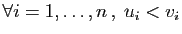 ,
,
-
 désigne le vecteur nul de
désigne le vecteur nul de
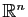 ,
,
-
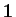 désigne le vecteur de
désigne le vecteur de
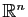 dont toutes les
coordonnées valent
dont toutes les
coordonnées valent  .
.
Soit 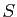 l'ensemble des réels
l'ensemble des réels
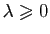 tels qu'il existe
tels qu'il existe
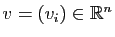 vérifiant :
vérifiant :
Soit 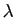 une valeur propre
de
une valeur propre
de  et
et 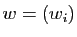 un vecteur propre associé. Pour tout
un vecteur propre associé. Pour tout
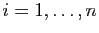 , posons
, posons 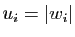 , puis
, puis
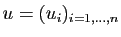 .
Par l'inégalité triangulaire :
.
Par l'inégalité triangulaire :
En divisant 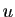 par la somme de ses coordonnées,
on en déduit que
par la somme de ses coordonnées,
on en déduit que 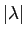 appartient à l'ensemble
appartient à l'ensemble 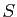 , qui est
donc non vide.
Pour tout
, qui est
donc non vide.
Pour tout
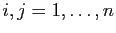 , notons
, notons 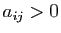 le coefficient d'ordre
le coefficient d'ordre
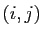 de
de  .
Tout élément
.
Tout élément 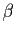 de
de 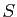 vérifie :
vérifie :
Donc
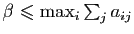 : l'ensemble
: l'ensemble 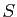 est borné.
Soit
est borné.
Soit 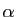 la borne supérieure de
la borne supérieure de 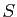 , et
, et
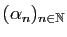 une suite d'éléments de
une suite d'éléments de 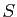 convergeant vers
convergeant vers
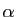 . À chacun des
. À chacun des 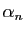 correspond un vecteur
correspond un vecteur 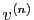 ,
dont les coordonnées sont positives ou nulles et de somme
,
dont les coordonnées sont positives ou nulles et de somme  , et tel
que
, et tel
que
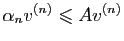 . Par le théorème de
Bolzano-Weierstrass, on peut extraire de la suite
. Par le théorème de
Bolzano-Weierstrass, on peut extraire de la suite
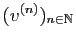 une
sous-suite
une
sous-suite
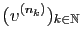 convergente. Soit
convergente. Soit 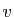 la limite de cette
sous-suite. Les coordonnées de
la limite de cette
sous-suite. Les coordonnées de
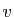 sont encore positives ou nulles et de somme
sont encore positives ou nulles et de somme  et en
particulier
et en
particulier 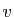 est non nul. En passant à la limite en
est non nul. En passant à la limite en 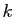 :
:
Supposons
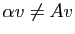 . Le vecteur
. Le vecteur
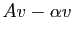 a toutes
ses coordonnées positives ou nulles et l'une au moins est non
nulle. Donc son produit par
a toutes
ses coordonnées positives ou nulles et l'une au moins est non
nulle. Donc son produit par  a toutes ses coordonnées strictement
positives (d'après l'hypothèse sur
a toutes ses coordonnées strictement
positives (d'après l'hypothèse sur  ) :
) :
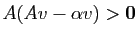 . Notons
. Notons 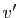 le vecteur proportionnel à
le vecteur proportionnel à
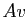 dont toutes les coordonnées sont positives ou nulles et de
somme
dont toutes les coordonnées sont positives ou nulles et de
somme  :
:
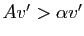 , donc il existe
, donc il existe
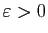 tel que
tel que
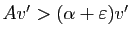 , ce qui contredit la définition de
, ce qui contredit la définition de 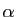 comme borne supérieure de
comme borne supérieure de 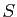 . On conclut donc que
. On conclut donc que
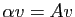 ,
donc
,
donc 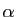 est valeur propre, et
est valeur propre, et 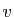 est un vecteur propre
associé à
est un vecteur propre
associé à 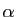 . A
priori, les coordonnées de
. A
priori, les coordonnées de 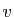 sont positives ou nulles. Mais alors
les coordonnées de
sont positives ou nulles. Mais alors
les coordonnées de 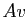 sont strictement positives. Puisque
sont strictement positives. Puisque
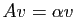 , on en conclut que
, on en conclut que 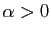 et
et
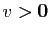 .
Montrons maintenant que
.
Montrons maintenant que 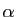 est strictement supérieure au
module de toute autre valeur propre. Soit
est strictement supérieure au
module de toute autre valeur propre. Soit 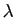 une valeur propre
de
une valeur propre
de  et
et 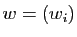 un vecteur propre associé. Nous avons déjà
montré que
un vecteur propre associé. Nous avons déjà
montré que
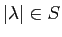 , en utilisant l'inégalité
triangulaire.
, en utilisant l'inégalité
triangulaire.
Comme 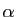 est la borne supérieure de
est la borne supérieure de 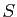 ,
,
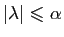 . Supposons
. Supposons
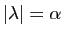 :
:
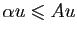 . Par le
raisonnement déjà effectué ci-dessus, on en conclut que
nécessairement
. Par le
raisonnement déjà effectué ci-dessus, on en conclut que
nécessairement
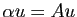 , donc les inégalités dans la
majoration ci-dessus sont en fait des égalités. Mais ceci n'est
possible que si
, donc les inégalités dans la
majoration ci-dessus sont en fait des égalités. Mais ceci n'est
possible que si 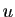 est proportionnel à
est proportionnel à 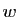 . Mais alors,
. Mais alors, 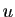 est
aussi vecteur propre associé à
est
aussi vecteur propre associé à 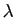 , donc
, donc
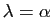 .
Il ne reste qu'un petit point à démontrer, mais c'est le plus
délicat :
.
Il ne reste qu'un petit point à démontrer, mais c'est le plus
délicat : 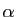 est valeur propre simple. Pour cela, nous
commençons par montrer que le sous-espace propre associé à
est valeur propre simple. Pour cela, nous
commençons par montrer que le sous-espace propre associé à
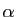 est une droite. Soit
est une droite. Soit 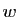 un vecteur propre associé à
un vecteur propre associé à
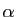 et comme ci-dessus
et comme ci-dessus 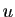 le vecteur des modules des
coordonnées de
le vecteur des modules des
coordonnées de 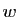 . Par un raisonnement déjà vu,
. Par un raisonnement déjà vu,
De sorte qu'aucun vecteur propre associé à 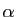 ne peut avoir
de coordonnée nulle. Mais si on pouvait trouver
deux vecteurs propres indépendants
associés à
ne peut avoir
de coordonnée nulle. Mais si on pouvait trouver
deux vecteurs propres indépendants
associés à 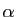 , alors on pourrait en former une
combinaison linéaire, qui serait encore vecteur propre associé à
, alors on pourrait en former une
combinaison linéaire, qui serait encore vecteur propre associé à
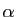 , et dont par exemple la première coordonnée serait
nulle. C'est impossible,
donc le sous-espace propre associé à
, et dont par exemple la première coordonnée serait
nulle. C'est impossible,
donc le sous-espace propre associé à 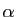 est de
dimension
est de
dimension  . Nous allons utiliser cela pour démontrer que
. Nous allons utiliser cela pour démontrer que
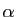 est racine simple du polynôme caractéristique
est racine simple du polynôme caractéristique
 .
Considérons le polynôme
.
Considérons le polynôme
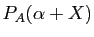 , qui est le déterminant
de
, qui est le déterminant
de
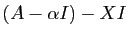 . Son terme constant, qui est le déterminant de
. Son terme constant, qui est le déterminant de
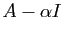 , est nul. Le coefficient du terme de degré
, est nul. Le coefficient du terme de degré  est la
trace (somme des coefficients diagonaux) de la comatrice de
est la
trace (somme des coefficients diagonaux) de la comatrice de
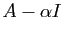 (matrice des mineurs
d'ordre
(matrice des mineurs
d'ordre 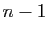 , affectés de signes alternés). Notons
, affectés de signes alternés). Notons 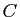 cette
comatrice. Comme le sous-espace propre associé à
cette
comatrice. Comme le sous-espace propre associé à 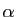 est de
dimension
est de
dimension  ,
,
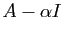 est de rang
est de rang 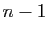 , donc la matrice
, donc la matrice 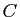 n'est pas nulle. Nous voulons démontrer que sa trace est non nulle.
Or
n'est pas nulle. Nous voulons démontrer que sa trace est non nulle.
Or
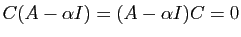 , car le déterminant de
, car le déterminant de
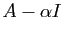 est nul. En particulier, tous les vecteurs colonnes de
est nul. En particulier, tous les vecteurs colonnes de 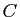 sont des
vecteurs propres de
sont des
vecteurs propres de  associés à
associés à 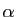 . En tant que tels, ils
sont proportionnels à
. En tant que tels, ils
sont proportionnels à 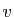 , dont toutes les coordonnées sont
strictement positives. Les vecteurs lignes sont des vecteurs propres
de
, dont toutes les coordonnées sont
strictement positives. Les vecteurs lignes sont des vecteurs propres
de 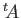 associés à
associés à 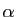 : ils sont donc également
proportionnels à un vecteur à coordonnées strictement positives.
Ceci entraîne que tous les coefficients de
: ils sont donc également
proportionnels à un vecteur à coordonnées strictement positives.
Ceci entraîne que tous les coefficients de
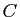 sont tous non nuls et de même signe
(tous strictement positifs ou tous strictement
négatifs). En particulier la trace est non nulle, et
sont tous non nuls et de même signe
(tous strictement positifs ou tous strictement
négatifs). En particulier la trace est non nulle, et 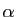 est
racine simple de
est
racine simple de 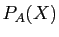 .
. Ferdinand Georg Frobenius (1849-1917) étendit en 1912 le théorème de
son jeune collègue
Perron aux matrices à coefficients positifs ou nuls, dont une
puissance entière a ses coefficients strictement positifs (matrices
irréductibles). C'est la version qui est à la base de la plupart
des applications, en particulier aux chaînes et processus de
Markov, mais nous aurons l'occasion de vous en reparler.
Ferdinand Georg Frobenius (1849-1917) étendit en 1912 le théorème de
son jeune collègue
Perron aux matrices à coefficients positifs ou nuls, dont une
puissance entière a ses coefficients strictement positifs (matrices
irréductibles). C'est la version qui est à la base de la plupart
des applications, en particulier aux chaînes et processus de
Markov, mais nous aurons l'occasion de vous en reparler.
Professeur à l'université de Tübingen, puis de Göttingen,
Perron est l'auteur de 218 articles, dont quelques uns
publiés après 80 ans,
ce qui est une longévité assez exceptionnelle. Il a par ailleurs
continué sa pratique assidue de l'alpinisme bien au-delà de 70 ans.
Quant à Frobenius, professeur à Zürich, puis Berlin, on lui doit
une grande partie de la théorie des matrices, en particulier
ce qui concerne les matrices compagnons. Il a montré
qu'une matrice quelconque est semblable à une matrice diagonale par
blocs, dont les blocs sont des matrices compagnons.
Il est resté célèbre
pour ses colères et ses opinions tranchées : voyez ce qu'il
écrit au sujet de Sophus Lie
(1842-1899).
Lie se contente de très peu de connaissances dans ses innombrables
papiers. Il a lu très peu de travaux des grands mathématiciens
classiques et en a compris encore moins. Ce que Lie nous fournit,
c'est une doctrine de méthodes de peu d'utilité, dont le
formalisme dénudé, qui à y bien penser nous rappelle les pires
moments de la théorie des invariants, doit rebuter tout lecteur au
goût éduqué.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
le plus grand entier naturel. Si
, alors
, ce qui contredit la définition. Donc
.
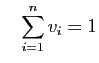 et
et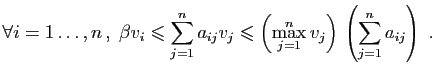
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales