Tout à l'envers

À partir de la définition axiomatique des espaces vectoriels, la notion de morphisme (application linéaire) s'ensuit. Dans le cas particulier de la dimension finie, pourvu que l'on ait choisi une base, les applications linéaires se représentent par des matrices. Une équation dont l'inconnue est un vecteur et la donnée une matrice est un système linéaire, que l'on peut résoudre à l'aide des déterminants. Le souci de représenter ces mêmes applications linéaires de la façon la plus simple possible conduit ensuite à la décomposition spectrale. Parmi les matrices admettant une décomposition spectrale simple se trouvent les matrices symétriques. Du moins est-ce ainsi que les choses vous ont été présentées. Mais l'histoire ne s'est pas déroulée dans le même ordre¹. Pour des calculs pratiques, on résoud des systèmes linéaires depuis la plus haute antiquité : la méthode du pivot de Gauss était déjà présente dans les «Neuf chapitres sur l'Art du calcul» en Chine au début de notre ère. Pourtant, la notion de déterminant n'a émergé qu'à la fin du XVII^e siècle, et n'a été vraiment formalisée qu'au début du XIX^e, trente ans après les formules de Cramer. Que le déterminant d'un produit de matrices soit le produit des deux déterminants de ces matrices a été démontré indépendamment par Binet et Cauchy en 1812, bien avant qu'il soit question de multiplier des matrices ou de composer des applications linéaires. Les mêmes calculs revenant assez souvent pour la résolution d'équations différentielles, en particulier en astronomie, ils ont été petit à petit systématisés, et c'est ainsi que les valeurs propres sont apparues. En 1829, Cauchy publie un article dont le titre en dit long sur ses péoccupations algébriques : «Sur l'équation avec laquelle on détermine les inégalités séculaires dans les mouvements des planètes». Il y calcule les maxima et minima d'une forme quadratique, ce qui le conduit tout droit au système

$$\left\{\begin{array}{lcl} A_{xx}x+A_{xy}y+A_{xz}z+\ldots&=&sx\\ ... ...y\\ A_{xz}x+A_{yz}y+A_{zz}z+\ldots&=&sx\\ \ldots&=&\ldots \end{array}\right.$$

Et un peu plus loin, comme une remarque en passant,

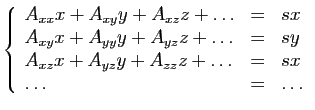
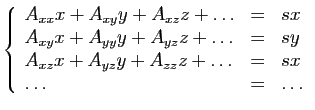
...on prouve facilement que l'équation (7) ne saurait admettre de racines imaginaires, tant que les coefficients $A_{xx}$, $A_{xy}$, $A_{xz}\ldots$; $A_{yy}$, $A_{yz}\ldots$, $A_{zz}\ldots$ restent réels. En effet...

Suit la première démonstration du fait que les valeurs propres d'une matrice symétrique sont réelles...plus de vingt ans avant que la notion de matrice ne soit introduite par Sylvester et Cayley, et avant que les valeurs propres aient été définies (indépendamment des matrices). Dès l'introduction de son article de 1858 «A memoir on the theory of matrices», Cayley annonce :

I obtain the remarkable theorem that any matrix whatever satisfies an algebraical equation of its own order, the coefficient of the highest power being unity, and those of the other powers functions of the terms of the matrix, the last coefficient being in fact the determinant; the rule for the formation of this equation may be stated in the following condensed form, which will be intelligible after a perusal of the memoir, viz. The determinant formed out of the matrix, diminished by the matrix considered as a single quantity involving the matrix unity, will be equal to zero.

C'est le théorème de Cayley-Hamilton... sans qu'il soit question encore de valeurs propres ! Quant aux espaces vectoriels et autres applications linéaires, ils apparaissent vers 1840, mais la relation entre matrices et applications linéaires n'est pas explicitée. D'ailleurs tout cela restera essentiellement confidentiel jusqu'à la fin du XIX^e. Il faudra attendre le début du XX^e pour que la puissance de l'algèbre linéaire soit reconnue, et les années 1930 pour qu'apparaissent les premiers livres qui l'exposent telle qu'elle vous est présentée.