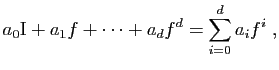
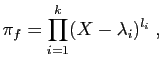
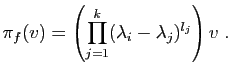
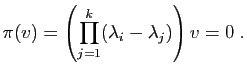
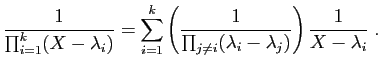
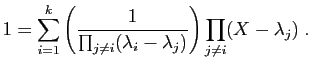
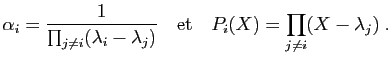
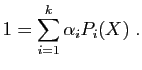
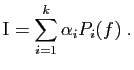
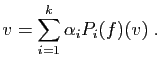
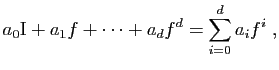
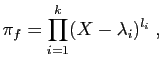
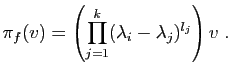
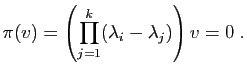
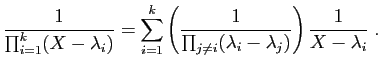
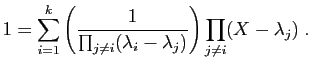
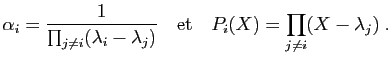
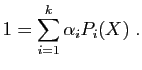
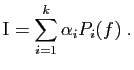
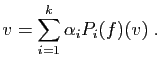
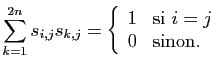
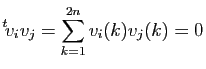 et
et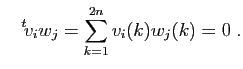
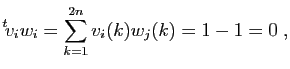
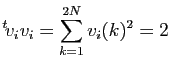 et
et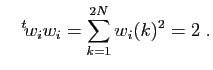
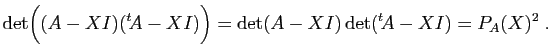
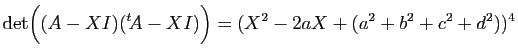
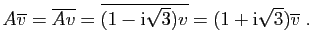
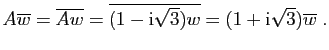
On doit vérifier que
![]() constitue
une base de
constitue
une base de
![]() . Pour cela, observons que les sous espaces
propres associés aux valeurs propres
. Pour cela, observons que les sous espaces
propres associés aux valeurs propres
![]() et
et
![]() sont d'intersection réduite à 0. Or les vecteurs
sont d'intersection réduite à 0. Or les vecteurs
![]() et
et ![]() ne sont pas proportionnels. Ils engendrent donc un
sous-espace vectoriel de dimension 2. De même
ne sont pas proportionnels. Ils engendrent donc un
sous-espace vectoriel de dimension 2. De même
![]() et
et
![]() engendrent un sous-espace vectoriel de dimension
engendrent un sous-espace vectoriel de dimension
![]() . Ces deux espaces sont en somme directe et ce sont des
sous-espaces de
. Ces deux espaces sont en somme directe et ce sont des
sous-espaces de
![]() . Leur somme est donc
. Leur somme est donc
![]() , et donc
, et donc
![]() est une famille génératrice de
est une famille génératrice de
![]() , donc une base. (On aurait pu aussi vérifier que c'est une
famille libre en calculant le
déterminant des 4 vecteurs, qui
vaut
, donc une base. (On aurait pu aussi vérifier que c'est une
famille libre en calculant le
déterminant des 4 vecteurs, qui
vaut
![]() ). Soit
). Soit ![]() la matrice dont les colonnes sont
la matrice dont les colonnes sont
![]() . Cette matrice est inversible, et
. Cette matrice est inversible, et
![]() , où
, où ![]() est la matrice diagonale dont les deux premiers
coefficients valent
est la matrice diagonale dont les deux premiers
coefficients valent
![]() , les deux suivants
, les deux suivants
![]() .
.
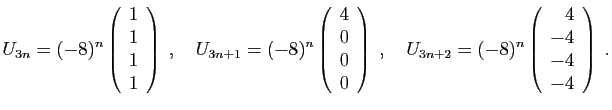
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales