QCM

Question 1 Soit une matrice $2\times 2$ , à coefficients réels.

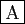
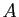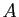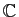$\framebox{A}$: Si admet une valeur propre complexe, alors est diagonalisable dans $\mathbb{C}$ .
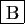
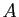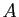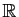$\framebox{B}$: Si admet une valeur propre réelle, alors est diagonalisable dans $\mathbb{R}$ .
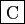
$\framebox{C}$: Si 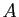admet une seule valeur propre, alors 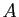est la matrice d'une homothétie.
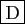
$\framebox{D}$: Si 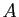n'est pas diagonalisable dans 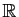$\mathbb{R}$ , alors 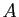admet une seule valeur propre.
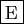
$\framebox{E}$: Si 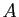admet au moins deux vecteurs propres distincts, alors 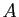est diagonalisable.

Question 2 Soit une matrice $3\times 3$ , à coefficients réels.

$\framebox{A}$: Si est diagonalisable dans $\mathbb{R}$ , alors toutes ses valeurs propres sont distinctes.
$\framebox{B}$: Si est triangulaire, alors toutes ses valeurs propres sont réelles.
$\framebox{C}$: Si admet deux valeurs propres complexes, alors est diagonalisable dans $\mathbb{C}$ .
$\framebox{D}$: Si admet au moins deux valeurs propres réelles distinctes, alors est diagonalisable dans $\mathbb{R}$ .
$\framebox{E}$: Si est symétrique, alors toutes ses valeurs propres sont distinctes.

Question 3 Soit une matrice de taille $n\times n$ ( $n\geqslant 2$ ), $\lambda$ une valeur propre de et sa multiplicité dans le polynôme caractéristique.

$\framebox{A}$: Si , alors le sous-espace propre associé à $\lambda$ est une droite vectorielle.
$\framebox{B}$: La dimension du sous-espace propre associé à $\lambda$ est toujours égale à .
$\framebox{C}$: La matrice $A-\lambda I$ est de rang .
$\framebox{D}$: Si le sous-espace propre associé à $\lambda$ est une droite vectorielle, alors .
$\framebox{E}$: Le sous-espace propre de associé à $\lambda$ est inclus dans le sous-espace propre de associé à $\lambda^2$ .

Question 4 Soit une matrice de taille $n\times n$ ( $n\geqslant 2$ ).

$\framebox{A}$: La somme des valeurs propres de est nulle si et seulement si son déterminant est nul.
$\framebox{B}$: Le produit des valeurs propres de est égal à son déterminant.
$\framebox{C}$: Les valeurs propres de et celles de sa transposée sont les mêmes.
$\framebox{D}$: Les sous-espaces propres de et ceux de sa transposée sont les mêmes.
$\framebox{E}$: Les sous-espaces propres de et ceux de sont les mêmes.

Question 5 Soit un endomorphisme de $\mathbb{R}^n$ ( $n\geqslant 2$ ), son polynôme caractéristique et $\pi_f$ son polynôme minimal.

$\framebox{A}$: Si est diagonalisable, alors toutes les racines de sont simples.
$\framebox{B}$: Si toutes les racines de $\pi_f$ sont simples, alors est diagonalisable.
$\framebox{C}$: Si $P_f=(-1)^n\pi_f$ , alors n'est pas diagonalisable.
$\framebox{D}$: Le degré de $\pi_f$ est toujours strictement inférieur au degré de .
$\framebox{E}$: Si a racines distinctes, alors $P_f=(-1)^n\pi_f$ .

Question 6 Soit un endomorphisme de $\mathbb{R}^n$ ( $n\geqslant 2$ ), son polynôme caractéristique et $\pi_f$ son polynôme minimal.

$\framebox{A}$: Si $\pi_f(X)=X^2-X$ alors est nilpotent.
$\framebox{B}$: Si $\pi_f(X)=X^2-1$ alors est une symétrie.
$\framebox{C}$: Si est une projection alors $\pi_f(X)=X^2$ .
$\framebox{D}$: Si $\pi_f(X)=X^2$ alors n'est pas diagonalisable.
$\framebox{E}$: Si $\pi_f(X)=X^2-X$ alors n'est pas diagonalisable.

Question 7 On considère la matrice $A=\left(\begin{array}{ccc} 1&0&0\\ 0&0&1\\ 0&0&0 \end{array}\right)$ .

$\framebox{A}$: La matrice est diagonalisable.
$\framebox{B}$: La matrice a deux valeurs propres distinctes.
$\framebox{C}$: La polynôme minimal de est .
$\framebox{D}$: Le sous espace propre associé à la valeur propre 0 est de dimension .
$\framebox{E}$: Il existe une matrice symétrique semblable à la matrice .

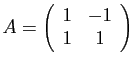
Question 8 On considère la matrice $A=\left(\begin{array}{ccc} 1&-1\\ 1&1 \end{array}\right)$ .

$\framebox{A}$: La matrice est diagonalisable dans $\mathbb{R}$
$\framebox{B}$: La matrice admet un vecteur propre à coordonnées réelles.
$\framebox{C}$: La somme des valeurs propres de est égale à leur produit.
$\framebox{D}$: Si $\lambda$ est valeur propre de , la première colonne de $A-\lambda I$ est vecteur propre de associé à $\lambda$ .
$\framebox{E}$: Si est vecteur propre de associé à $\lambda$ , alors $\overline{v}$ est vecteur propre de associé à $\overline{\lambda}$ .

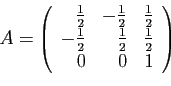
Question 9 On considère la matrice $\begin{displaymath} A = \left( \begin{array}{rrr} \frac{1}{2}&-\frac{1}{2}&\frac... ...frac{1}{2}&\frac{1}{2}&\frac{1}{2}\\ 0&0&1 \end{array}\right) \end{displaymath}$ .

$\framebox{A}$: La matrice a trois valeurs propres distinctes.
$\framebox{B}$: Le sous-espace propre associé à la valeur propre est de dimension .
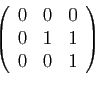
$\framebox{C}$: La matrice est semblable à la matrice $\begin{displaymath} \left( \begin{array}{rrr} 0&0&0\\ 0&1&1\\ 0&0&1 \end{array}\right) \end{displaymath}$ .
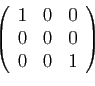
$\framebox{D}$: La matrice est semblable à la matrice $\begin{displaymath} \left( \begin{array}{rrr} 1&0&0\\ 0&0&0\\ 0&0&1 \end{array}\right) \end{displaymath}$ .
$\framebox{E}$: Le polynôme minimal de est de degré .

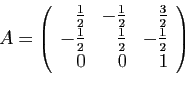
Question 10 On considère la matrice $\begin{displaymath} A = \left( \begin{array}{rrr} \frac{1}{2}&-\frac{1}{2}&\frac... ...rac{1}{2}&\frac{1}{2}&-\frac{1}{2}\\ 0&0&1 \end{array}\right) \end{displaymath}$ .

$\framebox{A}$: La matrice a deux valeurs propres distinctes.
$\framebox{B}$: Le sous-epace propre associé à la valeur propre est de dimension .
$\framebox{C}$: La matrice est semblable à la matrice $\begin{displaymath} \left( \begin{array}{rrr} 1&0&0\\ 0&0&0\\ 0&0&1 \end{array}\right) \end{displaymath}$ .
$\framebox{D}$: Le polynôme minimal de est de degré .
$\framebox{E}$: La matrice est semblable à la matrice $\begin{displaymath} \left( \begin{array}{rrr} 0&0&0\\ 0&1&1\\ 0&0&1 \end{array}\right) \end{displaymath}$ .

$\framebox{\rotatebox{180}{Réponses : 1-AD 2-BC 3-AE 4-BC 5-BE 6-BD 7-BC 8-CE 9-BD 10-AE}}$