Premier point à observer : l'arithmétique sur les polynômes est tout à fait analogue à celle sur les entiers à condition de travailler sur des polynômes sur un corps commutatif. Sur un anneau commutatif quelconque (même intègre) se glissent quelques bizarreries.
Second point à observer : les énoncés donnés sur les
entiers l'ont été
sur des entiers positifs. Ils se modifient sans trop de mal pour des
entiers de
![]() mais parfois en s'alourdissant un peu ; ainsi dans
mais parfois en s'alourdissant un peu ; ainsi dans
![]() on ne peut plus affirmer l'existence d'un entier
on ne peut plus affirmer l'existence d'un entier ![]() unique tel
que
unique tel
que ![]() divise
divise ![]() et
et ![]() si et seulement si
si et seulement si ![]() divise
divise ![]() (le pgcd
de
(le pgcd
de ![]() et
et ![]() ) : il en existe toujours un, mais il n'est plus unique,
on peut prendre
) : il en existe toujours un, mais il n'est plus unique,
on peut prendre ![]() mais aussi
mais aussi ![]() . Les polynômes unitaires
joueront un rôle analogue aux entiers positifs mais ils sont
légèrement moins confortables, dans la mesure où la somme de deux
entiers positifs est positive alors que la somme de deux polynômes
unitaires n'est pas nécessairement unitaire. Attention à ces petits
détails donc, en apprenant les énoncés.
. Les polynômes unitaires
joueront un rôle analogue aux entiers positifs mais ils sont
légèrement moins confortables, dans la mesure où la somme de deux
entiers positifs est positive alors que la somme de deux polynômes
unitaires n'est pas nécessairement unitaire. Attention à ces petits
détails donc, en apprenant les énoncés.
Commençons par donner une définition, à partir de laquelle on ne
montrera guère de théorèmes que dans
![]() mais
que ça ne coûte pas
plus cher de donner sur un anneau commutatif quelconque.
mais
que ça ne coûte pas
plus cher de donner sur un anneau commutatif quelconque.
Comme pour les entiers, tout repose sur la division euclidienne.
Démonstration : On prouvera successivement l'existence et l'unicité de ![]() .
.
Existence de ![]()
La preuve est significativement différente de celle utilisée pour les entiers. Elle est toujours basée sur une maximisation/minimisation, mais les polynômes n'étant pas totalement ordonnés, cette maximisation est un peu plus technique.
Dans le cas stupide où ![]() divise
divise ![]() , prenons
, prenons ![]() et
et ![]() tel que
tel que
![]() . Sinon, considérons l'ensemble
. Sinon, considérons l'ensemble
Nous devons vérifier que ces choix conviennent ;
l'identité entre ![]() ,
, ![]() ,
, ![]() et
et ![]() est
claire, reste l'inégalité concernant les degrés.
Vérifions-la par l'absurde, en supposant
que
est
claire, reste l'inégalité concernant les degrés.
Vérifions-la par l'absurde, en supposant
que
![]() ; notons
; notons ![]() le degré de
le degré de ![]() et
et
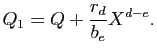
Considérons alors
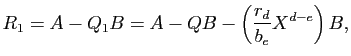
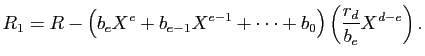
Unicité de ![]()
Soient ![]() et
et ![]() deux couples
vérifiant les deux conditions exigées
dans l'énoncé du théorème.
deux couples
vérifiant les deux conditions exigées
dans l'énoncé du théorème.
On déduit de
![]() que
que
![]() . Ainsi,
. Ainsi,
![]() est un multiple de
est un multiple de ![]() .
Des conditions
.
Des conditions
![]() et
et
![]() , on déduit que
, on déduit que
![]() .
.
Ainsi ![]() est un multiple de
est un multiple de ![]() de degré strictement
plus petit. La seule
possibilité est que
de degré strictement
plus petit. La seule
possibilité est que
![]() soit nul. On en déduit
soit nul. On en déduit ![]() , puis, en allant
reprendre l'égalité
, puis, en allant
reprendre l'égalité
![]() , que
, que
![]() .
.![]()
Remarque : On a choisi d'énoncer ce théorème sur un corps commutatif
pour faciliter sa mémorisation et parce que l'on n'aura presque jamais
besoin d'un énoncé plus général. On aura toutefois besoin une fois de
l'utiliser pour des polynômes sur un anneau ; remarquons donc que la
démonstration montre que le résultat reste vrai sur un anneau
commutatif quelconque à condition de supposer non seulement que ![]() est non nul, mais même que son coefficient dominant est inversible :
le seul endroit où on a utilisé qu'on s'était placé dans un corps
commutatif a en effet été une division par ce coefficient dominant.
est non nul, mais même que son coefficient dominant est inversible :
le seul endroit où on a utilisé qu'on s'était placé dans un corps
commutatif a en effet été une division par ce coefficient dominant.
Nous définissons ensuite le pgcd.
On ne donnera pas ici d'énoncés concernant le
![]() , non qu'il n'y
en ait pas (ce sont là aussi les mêmes qu'en arithmétique des
entiers) mais parce qu'ils ne semblent pas très importants. Les
étudiants curieux les reconstitueront eux-mêmes.
, non qu'il n'y
en ait pas (ce sont là aussi les mêmes qu'en arithmétique des
entiers) mais parce qu'ils ne semblent pas très importants. Les
étudiants curieux les reconstitueront eux-mêmes.
De plus il existe deux polynômes
![]() et
et ![]() de
de
![]() tels que
tels que ![]() (identité de Bézout).
(identité de Bézout).
Et tant qu'on y est avant de passer aux démonstrations :
Comme pour les entiers, plusieurs démonstrations sont possibles ; on ne donne que celle basée sur l'algorithme d'Euclide.
Démonstration : La démonstration est une récurrence sur le degré de ![]() .
.
Merveilles du copier-coller, voici de nouveau un «résumé de la preuve» sous forme de programme informatique récursif (le même que pour l'arithmétique des entiers) :
Début du programme
* Pour ![]() ,
,
![]() coefficient dominant de
coefficient dominant de ![]() .
.
* Soit ![]() le reste de la division euclidienne de
le reste de la division euclidienne de ![]() par
par ![]() .
.
Les diviseurs communs de ![]() et
et ![]() sont ceux de
sont ceux de ![]() et
et ![]() .
.
D'où :
![]() .
.
Fin du programme
Et voici, toujours par les vertus du copier-coller,
la preuve récurrente formelle.
On va démontrer par «récurrence forte» sur le
degré ![]() de
de ![]() l'hypothèse
l'hypothèse
![]() suivante :
suivante :
Pour tout polynôme
et tout polynôme
de degré
, il existe deux polynômes
et
tels que, pour tout polynôme
,
divise
et
si et seulement si
divise
.
Vérifions
![]() .
.
Il s'agit donc de traiter le cas où ![]() . Soit
. Soit ![]() un
polynôme ; tout polynôme
un
polynôme ; tout polynôme ![]() qui divise
qui divise
![]() divise aussi
divise aussi ![]() puisque
puisque ![]() . Pour tout
. Pour tout ![]() ,
, ![]() divise
divise ![]() et 0 si et seulement si
et 0 si et seulement si ![]() divise
divise ![]() .
Prenons alors
.
Prenons alors ![]() et
et ![]() : on a donc
bien pour tout
: on a donc
bien pour tout ![]() :
: ![]() divise
divise ![]() et 0 si et seulement si
et 0 si et seulement si ![]() divise
divise
![]() .
.
Soit ![]() un entier fixé. Supposons la propriété
un entier fixé. Supposons la propriété
![]() vraie pour tout
vraie pour tout ![]() strictement inférieur
à
strictement inférieur
à ![]() et montrons
et montrons ![]() .
.
Soient ![]() un polynôme et
un polynôme et ![]() un polynôme de degré
un polynôme de degré ![]() .
Notons
.
Notons ![]() la division
euclidienne de
la division
euclidienne de ![]() par
par ![]() (qu'on peut réaliser puisque
(qu'on peut réaliser puisque ![]() ).
).
Vérifions l'affirmation intermédiaire suivante : pour tout ![]() ,
,
![]() est un diviseur commun de
est un diviseur commun de ![]() et
et ![]() si et seulement si
si et seulement si
![]() est un diviseur commun de
est un diviseur commun de ![]() et
et
![]() . (Avec des mots peut-être plus lisibles :
«les diviseurs communs de
. (Avec des mots peut-être plus lisibles :
«les diviseurs communs de ![]() et
et
![]() sont les mêmes que ceux de
sont les mêmes que ceux de ![]() et
et ![]() »).
»).
Soit ![]() un diviseur commun de
un diviseur commun de ![]() et
et ![]() , alors
, alors ![]() divise aussi
divise aussi
![]() ; réciproquement soit
; réciproquement soit ![]() un diviseur
commun de
un diviseur
commun de ![]() et
et ![]() , alors
, alors ![]() divise aussi
divise aussi ![]() .
.
L'affirmation intermédiaire est donc démontrée.
On peut alors appliquer l'hypothèse de récurrence
![]() (puisque
précisément
(puisque
précisément
![]() ) en l'appliquant au polynôme
) en l'appliquant au polynôme ![]() .
.
On en déduit qu'il existe deux polynômes ![]() et
et ![]() tels que pour tout
tels que pour tout ![]() ,
, ![]() divise
divise ![]() et
et ![]() si et seulement si
si et seulement si ![]() divise
divise
![]() .
.
Remarquons enfin que
![]() , et qu'ainsi, si on pose
, et qu'ainsi, si on pose ![]() et
et ![]() on a bien
prouvé que, pour tout
on a bien
prouvé que, pour tout ![]() ,
, ![]() divise
divise ![]() et
et ![]() si et seulement si
si et seulement si ![]() divise
divise ![]() .
.
![]() est donc démontrée.
est donc démontrée.
On a donc bien prouvé ![]() pour tout
pour tout
![]() .
.
Une fois qu'on en est arrivé là, il ne reste donc plus
qu'à montrer que pour un
polynôme ![]() (le polynôme
(le polynôme ![]() ) il existe un
unique
) il existe un
unique ![]() unitaire tel que
unitaire tel que ![]() divise
divise ![]() si et seulement si
si et seulement si ![]() divise
divise ![]() . L'existence est
claire : comme le résumé le suggère, on
divise
. L'existence est
claire : comme le résumé le suggère, on
divise ![]() par son coefficient dominant et on
obtient un polynôme
par son coefficient dominant et on
obtient un polynôme ![]() unitaire ayant les mêmes
diviseurs que
unitaire ayant les mêmes
diviseurs que ![]() . Pour ce qui est de l'unicité,
elle est évidente pour
. Pour ce qui est de l'unicité,
elle est évidente pour ![]() nul ; on
supposera
nul ; on
supposera ![]() non nul. Soit
maintenant
non nul. Soit
maintenant ![]() un polynôme unitaire ayant
exactement les mêmes diviseurs que
un polynôme unitaire ayant
exactement les mêmes diviseurs que ![]() . Alors comme
. Alors comme
![]() divise
divise ![]() ,
, ![]() divise
divise ![]() , et comme
, et comme ![]() divise
divise ![]() ,
,
![]() divise
divise ![]() . Les polynômes
. Les polynômes ![]() et
et ![]() se divisent donc mutuellement ; soit
se divisent donc mutuellement ; soit ![]() et
et ![]() les quotients respectifs de
les quotients respectifs de ![]() par
par ![]() et de
et de
![]() par
par ![]() . En utilisant la formule calculant
le degré d'un produit, on voit que forcément,
. En utilisant la formule calculant
le degré d'un produit, on voit que forcément,
![]() a même degré que
a même degré que ![]() et que les polynômes
et que les polynômes
![]() et
et ![]() sont de degré nul, donc des
constantes
sont de degré nul, donc des
constantes ![]() et
et ![]() . Soit
. Soit ![]() le
coefficient dominant de
le
coefficient dominant de
![]() ; le coefficient dominant de
; le coefficient dominant de ![]() vaut
vaut
![]() donc
donc
![]() et
et
![]() est égal à
est égal à ![]() (coefficient dominant de
(coefficient dominant de ![]() ),
donc à
),
donc à ![]() , ce qui prouve l'unicité.
, ce qui prouve l'unicité.![]()
Nous allons ensuite définir le pgcd d'un nombre fini de polynômes. En arithmétique des entiers, cette notion n'est pas primordiale ; en revanche dans les applications des raisonnements arithmétiques à des polynômes, on est souvent dans des cas où on s'intéresse à des pgcds de plus de deux polynômes à la fois.
L'énoncé donné ci-dessus pour deux polynômes se généralise à un nombre fini, par récurrence sur ce nombre.
De plus il existe ![]() polynômes
polynômes
![]() tels que
tels que
Démonstration : C'est une récurrence facile sur ![]() . Le cas
. Le cas ![]() est
l'objet du théorème précédent (et le cas
est
l'objet du théorème précédent (et le cas ![]() a été traité dans sa démonstration,
ou on peut le ramener fictivement
à
a été traité dans sa démonstration,
ou on peut le ramener fictivement
à ![]() en disant que les diviseurs de
en disant que les diviseurs de ![]() sont
les diviseurs communs de
sont
les diviseurs communs de ![]() et de 0).
et de 0).
Soit
![]() fixé, supposons la proposition vraie
pour tout ensemble de
fixé, supposons la proposition vraie
pour tout ensemble de ![]() polynômes. Prenons
polynômes. Prenons ![]() polynômes
polynômes
![]() .
Notons
.
Notons ![]() le pgcd des
le pgcd des ![]() premiers, qui existe par
l'hypothèse de récurrence. Alors les diviseurs
communs de
premiers, qui existe par
l'hypothèse de récurrence. Alors les diviseurs
communs de ![]() ,
, ![]() ,
, ![]() ,
, ![]() sont les
diviseurs communs de
sont les
diviseurs communs de ![]() et de
et de ![]() ; donc
prendre
; donc
prendre
![]() répond à
la question. L'unicité est claire : si
répond à
la question. L'unicité est claire : si ![]() répondait
aussi à la question, les diviseurs de
répondait
aussi à la question, les diviseurs de
![]() seraient exactement les mêmes que ceux de
seraient exactement les mêmes que ceux de ![]() avec
avec ![]() et
et ![]() tous deux unitaires, et
comme dans la preuve du théorème précédent
(ou en appliquant le théorème précédent à
tous deux unitaires, et
comme dans la preuve du théorème précédent
(ou en appliquant le théorème précédent à ![]() et
0), on conclut que
et
0), on conclut que ![]() . La relation de Bézout
est aussi le résultat d'une récurrence
immédiate : il existe
. La relation de Bézout
est aussi le résultat d'une récurrence
immédiate : il existe
![]() tels
que
tels
que
![]() et
et
![]() et
et ![]() tels que
tels que
![]() donc
donc
On prendra garde à ne pas confondre «premiers entre eux»
(on dit parfois «premiers entre eux dans leur ensemble»)
et «deux à deux premiers entre eux»
: dans
![]() , les polynômes
, les polynômes
Les polynômes irréductibles sont les analogues des nombres premiers. Toutefois les usages étant ce qu'ils sont, il y a une petite nuance de vocabulaire un peu désagréable : alors que le mot «nombre premier» est réservé à des entiers positifs, le mot «polynôme irréductible» n'est pas réservé à des polynômes unitaires. On se méfiera de cette peu perceptible nuance qui crée de légères discordances entre énoncés analogues portant les uns sur les polynômes et les autres sur les entiers.
On remarquera tout de suite que ces deux diviseurs unitaires
sont alors forcément les polynômes
![]() et
et ![]() (coefficient dominant de
(coefficient dominant de ![]() ).
).
La proposition suivante est évidente, mais donne un exemple fondamental de polynômes irréductibles :
Démonstration : Soit ![]() avec
avec ![]() un polynôme du premier
degré dans
un polynôme du premier
degré dans
![]() . Cherchons ses diviseurs
unitaires. Un diviseur de
. Cherchons ses diviseurs
unitaires. Un diviseur de ![]() doit avoir un
degré inférieur ou égal à
celui de
doit avoir un
degré inférieur ou égal à
celui de ![]() . Le seul diviseur unitaire constant de
. Le seul diviseur unitaire constant de
![]() est le seul polynôme constant unitaire :
la constante
est le seul polynôme constant unitaire :
la constante ![]() . Cherchons les diviseurs unitaires
de la forme
. Cherchons les diviseurs unitaires
de la forme ![]() de
de ![]() . Si
. Si ![]() divise
divise ![]() ,
il existe un polynôme
,
il existe un polynôme ![]() tel que
tel que ![]() et
en comparant les degrés,
et
en comparant les degrés, ![]() est nécessairement
constant. En comparant les coefficients
dominants, nécessairement
est nécessairement
constant. En comparant les coefficients
dominants, nécessairement ![]() donc
donc
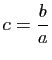 . Ainsi
. Ainsi ![]() possède exactement
un diviseur unitaire du premier degré, le polynôme
possède exactement
un diviseur unitaire du premier degré, le polynôme
 . Le polynôme
. Le polynôme ![]() est donc irréductible.
est donc irréductible.![]()
Sur un corps quelconque, déterminer quels polynômes sont irréductibles et lesquels ne le sont pas est un problème très sérieux ; dans quelques pages, nous verrons que ce problème a une solution simple dans les cas particuliers des polynômes à coefficients complexes ou réels.
Le résultat fondamental est, comme en arithmétique entière,
l'existence et unicité de la
décomposition en facteurs irréductibles. Elle repose
là encore sur le «lemme de Gauss». On ne
réécrit pas les démonstrations pour deux raisons
totalement contradictoires : d'abord parce que
ce sont exactement les mêmes, et ensuite parce que
ce ne sont pas exactement les mêmes -une
petite difficulté se pose pour énoncer l'unicité
de la décomposition en facteurs irréductibles
d'un polynôme. Pour des entiers, on a convenu de classer
les facteurs dans l'ordre croissant :
ainsi ![]() se décompose en
se décompose en ![]() et
non en
et
non en ![]() . Une telle convention ne peut être
appliquée pour décomposer des polynômes,
aucun ordre «raisonnable» n'étant à notre disposition
sur l'ensemble des polynômes irréductibles ;
ainsi dans
. Une telle convention ne peut être
appliquée pour décomposer des polynômes,
aucun ordre «raisonnable» n'étant à notre disposition
sur l'ensemble des polynômes irréductibles ;
ainsi dans
![]() peut-on écrire selon la
fantaisie du moment
peut-on écrire selon la
fantaisie du moment
![]() ou
ou
![]() .
Quand on énonce ci-dessous que la
décomposition est «unique» on sous-entend donc
qu'on considère les deux exemples qui précèdent
comme la même décomposition, ce qui peut s'énoncer
rigoureusement mais lourdement. Voulant
glisser sur ce détail, on se condamne à rester un peu vaseux.
.
Quand on énonce ci-dessous que la
décomposition est «unique» on sous-entend donc
qu'on considère les deux exemples qui précèdent
comme la même décomposition, ce qui peut s'énoncer
rigoureusement mais lourdement. Voulant
glisser sur ce détail, on se condamne à rester un peu vaseux.
Voici donc le lemme de Gauss.
Démonstration : La même que pour les entiers, avec des majuscules.![]()
Et voici le théorème de décomposition en facteurs irréductibles.
Démonstration : À peu près la même que pour les entiers, avec un peu plus de soin
pour l'unicité.![]()
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales