Section : Cours
Avant : Cours
Après : Arithmétique des polynômes

Anneau des polynômes

L'idée de la construction sera peut-être compréhensible si on se demande comment stocker une fonction polynomiale de $ \mathbb{R}$ dans $ \mathbb{R}$ dans une mémoire de machine : stocker toutes les valeurs de la fonction étant impossible, un bon procédé pour représenter la fonction $ t\mapsto 4+5t^2+7t^3+t^5$, par exemple, sera de stocker la suite de ses coefficients ; on entrera donc dans la machine la suite $ 405701$, ce qui indique que le coefficient de $ t^0$ est $ 4$, celui de $ t$ est 0, celui de $ t^2$ est $ 5$, etc.

Ce procédé de stockage sera tout bonnement la définition même des polynômes. Simplement, comme un polynôme peut en théorie être de degré gigantesque, bien plus grand que les capacités de stockage de toute machine, il faudra se résigner à stocker une infinité de coefficients, dont seuls les $ N$ premiers seront non nuls (la métaphore technologique s'écroule alors) : ainsi notre polynôme-exemple sera stocké comme $ 4057010000\ldots$ (puis encore une infinité de 0), occupant inutilement une infinité de cases-mémoire.

Définition 1   Soit $ (A,+)$ un groupe de neutre 0. Une suite $ (a_{n})_{n\in\mathbb{N}}$ d'éléments de $ A$ est dite à support fini, ou bien nulle à partir d'un certain rang, si le nombre d'indices $ n$ pour lesquels $ a_{n}\neq 0$ est fini. En d'autres termes, il existe un indice $ N$ fini tel que $ a_{n}\neq 0$ implique $ n\leqslant N$.

Définition 2   Soit $ (A,+,\cdot)$ un anneau commutatif. Notons provisoirement $ B$ l'ensemble des suites d'éléments de $ A$, à support fini. On définit sur $ B$ une addition et une multiplication par les formules

$\displaystyle (a_n)_{n \in\mathbb{N}}+(b_n)_{n\in\mathbb{N}}=(a_n+b_n)_{n\in\mathbb{N}}, $

et

$\displaystyle (a_n)_{n\in\mathbb{N}}\cdot(b_n)_{n\in\mathbb{N}}=(c_n)_{n\in\mathbb{N}}\qquad\hbox{o\\lq u}\quad c_n=\sum_{k=0}^na_kb_{n-k}. $

Proposition 1   L'ensemble $ B$ muni des deux lois définies ci-dessus est un anneau commutatif.

Démonstration : Il est facile de vérifier que $ (B,+)$ est un sous-groupe du groupe abélien (additif) de toutes les suites d'éléments de $ A$. En effet, le neutre de $ A$ est la suite identiquement nulle, qui appartient à $ B$ ; la somme de deux suites à supports finis est à support fini : si $ a_{n}=0$ pour tout $ n>N$ et si $ b_{n}=0$ pour tout $ n>M$, alors $ a_{n}+b_{n}=0$ pour tout $ n>\max\{N,M\}$ (et peut-être pour d'autres indices $ n$ également mais ce n'est pas important) ; enfin si $ -a$ désigne l'opposé d'un élément $ a$ de $ A$, alors l'opposé d'un élément $ (a_{n})_{n\in\mathbb{N}}$ de $ B$ est la suite $ (-a_{n})_{n\in\mathbb{N}}$, qui est effectivement à support fini.

Pour ce qui concerne la deuxième loi, on doit tout d'abord vérifier que $ (c_n)_{n\in\mathbb{N}}$ est bien une suite de $ B$. Avec les mêmes notations que pour l'addition, pour tout indice $ n>M+N$, dans le calcul de

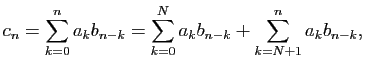
$\displaystyle c_n=\sum_{k=0}^n a_kb_{n-k}= \sum_{k=0}^N a_kb_{n-k}+\sum_{k=N+1}^n a_kb_{n-k}, $

tous les termes de la première somme sont nuls, car les indices utilisés sont tels que $ n-k>M+N-k\geqslant M$ donc $ b_{n-k}=0$. Tous les termes de la deuxième somme sont nuls aussi car $ k>N$ donc $ a_k=0$. Tous les coefficients $ c_n$ pour $ n>M+N$ sont donc nuls et $ (c_n)_{n\in\mathbb{N}}$ est bien un élément de $ B$.

On va ensuite vérifier que pour ces formules, $ B$ est un anneau commutatif. C'est peu engageant et il n'y a guère d'astuces. Il faut calculer brutalement.

Commutativité

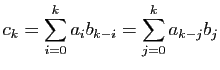Soient $ (a_i)_{i \in\mathbb{N}}$ et $ (b_j)_{j\in\mathbb{N}}$ deux éléments de $ B$ ; notons $ (c_k)_{k\in\mathbb{N}}$ le produit de $ (a_i)_{i \in\mathbb{N}}$ par $ (b_j)_{j\in\mathbb{N}}$. Alors pour tout $ k\geqslant 0$, $ c_k=\displaystyle\sum_{i=0}^ka_ib_{k-i}= \displaystyle\sum_{j=0}^ka_{k-j}b_j$ (en posant $ j=k-i$) ; cette expression est bien celle qu'on trouverait en faisant le produit dans l'autre sens (en utilisant la commutativité de $ A$).

Associativité

Soient $ (a_n)_{n\in\mathbb{N}}$, $ (b_n)_{n\in\mathbb{N}}$ et $ (c_n)_{n\in\mathbb{N}}$ trois éléments de $ B$ ; notons $ (d_n)_{n\in\mathbb{N}}$ le produit de $ (b_n)_{n\in\mathbb{N}}$ par $ (c_n)_{n\in\mathbb{N}}$. Notons $ (e_n)_{n\in\mathbb{N}}$ le produit de $ (a_n)_{n\in\mathbb{N}}$ par $ (d_n)_{n\in\mathbb{N}}$. Pour $ n\geqslant 0$, calculons

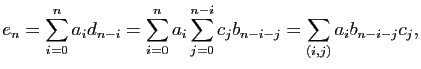
$\displaystyle e_n=\sum_{i=0}^na_id_{n-i}=\sum_{i=0}^na_i\sum_{j=0}^{n-i}c_jb_{n-i-j}= \sum_{(i,j)}a_ib_{n-i-j}c_j, $

où la dernière somme porte sur tous les couples $ (i,j)\in\mathbb{N}^2$ tels que $ i+j\leqslant n$.

On trouverait la même chose en calculant de la même façon le produit de $ (a_n)_{n\in\mathbb{N}}\cdot(b_n)_{n\in\mathbb{N}}$ par $ (c_n)_{n\in\mathbb{N}}$.

Existence d'un élément neutre

La suite $ (1,0,0,0,\ldots)$ est neutre pour cette multiplication.

Distributivité

Encore une vérification ennuyeuse, celle-là on va l'omettre.

On a bien vérifié que $ B$ est un anneau commutatif.$ \square$

Notation 1   On note 0 la suite nulle. On appelle indéterminée l'élément

$\displaystyle (0,1,0,0,\ldots) $

de $ B$ dont tous les termes sont nuls sauf le terme de numéro $ 1$ qui vaut $ 1$. On note souvent (mais pas toujours) $ X$ l'indéterminée.

Proposition 2   Pour tout élément $ P$ de $ B$ tel que $ P\not=0$, il existe un unique entier $ d\geqslant 0$ et un unique $ (d+1)$-uplet $ (a_i)_{0\leqslant i\leqslant d}$ d'éléments de $ A$ tels que $ a_d\not=0$ et

$\displaystyle P=a_dX^d+a_{d-1}X^{d-1}+\cdots+a_1X+a_0. $

Démonstration : Il suffit de remarquer que, pour tout $ n\geqslant 1$, $ X^{n}$ est la suite dont tous les termes sont nuls sauf le terme de numéro $ n$ qui vaut $ 1$. Ensuite, on réécrit les définitions.$ \square$

Notation 2   Si $ X$ est l'indéterminée de $ B$, on note $ B=A[X]$ et on appelle $ A[X]$ l'anneau des polynômes sur $ A$.

Profitons-en pour faire quelques calculs.

Exemple 1   Soient $ P=X^{3}-3X^{2}+2$ et $ Q=X^{2}-X+2$. Il s'agit de calculer le polynôme $ PQ$.

On pourra décomposer un des deux polynômes, par exemple $ Q$, en somme de monômes, donc $ X^{2}$, $ -X$ et $ 2$, puis effectuer chacune des multiplications de $ P$ par ces monômes, et enfin tout regrouper. Une présentation claire, en alignant les monômes de mêmes degrés, est une condition nécessaire de calcul sans erreurs.

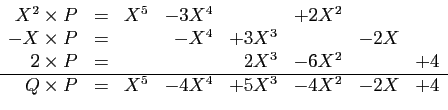
\begin{displaymath} \begin{array}{rcrrrrrr} X^2\times P & = & X^5&-3X^4&&+2X^2&&... ...\ \hline Q\times P &=&X^5&-4X^4&+5X^3&-4X^2&-2X&+4 \end{array}\end{displaymath}

Définition 3   Pour tout élément $ P$ non nul de $ A[X]$, l'unique entier $ d\geqslant 0$ intervenant dans l'écriture de $ P$ en fonction de l'indéterminée dans la proposition 2 est appelé le degré de $ P$. Par convention, le degré du polynôme nul est le symbole $ -\infty$.

Notation 3   Le degré d'un polynôme $ P$ est noté $ \deg P$.

Définition 4   Pour $ P$ élément non nul de $ A[X]$, le coefficient dominant de $ P$ est le coefficient $ a_d$ du terme de plus haut degré dans l'écriture de $ P$ en fonction de l'indéterminée. Par convention, le coefficient dominant du polynôme nul est 0. Enfin, un polynôme est dit unitaire lorsque son coefficient dominant est égal à $ 1$.

Proposition 3   Soient $ P$ et $ Q$ deux polynômes de $ A[X]$. Alors :

$\displaystyle \deg (P+Q)\leqslant\max(\deg P,\deg Q). $

Démonstration : Si $ P$ ou $ Q$ est nul, le résultat est évident. Sinon, notons $ d$ le degré de $ P$ et $ e$ le degré de $ Q$ puis $ P=a_dX^d+\cdots+a_0$ et $ Q=b_eX^e+\cdots+b_0$ pour des $ a_i$ et $ b_i$ dans $ A$. Si $ d>e$, on peut alors écrire :

$\displaystyle P+Q=a_dX^d+\cdots+a_{e+1}X^{e+1}+(a_e+b_e)X^e+\cdots+(a_0+b_0). $

Il apparaît alors que $ \deg (P+Q)=d=\max(\deg P,\deg Q)$. Le cas où $ d<e$ est similaire. Enfin, lorsque $ d=e$, on a un regroupement :

$\displaystyle P+Q=(a_d+b_d)X^d+\cdots+(a_0+b_0).$

Ou bien tous les coefficients y sont nuls, et $ \deg(P+Q)=-\infty$ rendant l'inégalité évidente, ou bien un au moins est non nul et le coefficient non nul de plus fort indice est le degré de $ P+Q$ qui est bien inférieur ou égal à $ d$.$ \square$

Proposition 4   Soit $ A$ est un anneau commutatif intègre (sans diviseur de zéro). Soient $ P$ et $ Q$ deux polynômes de $ A[X]$. Alors :

$\displaystyle \deg (PQ)=\deg P+\deg Q. $

Remarque : Pour un anneau non intègre, on a encore une inégalité, mais cela ne semble pas indispensable à mémoriser (d'autant que la preuve en est très facile).

Démonstration : Essentiellement déjà faite.

Si $ P$ ou $ Q$ est nul, c'est évident ; sinon notons $ d$ le degré de $ P$ et $ e$ le degré de $ Q$ puis $ P=a_dX^d+\cdots+a_0$ et $ Q=b_eX^e+\cdots+b_0$ pour des $ a_i$ et $ b_i$ dans $ A$. On a alors

$\displaystyle PQ=a_db_eX^{d+e}+({a_db_{e-1}+a_{d-1}b_e})X^{d+e-1}+\cdots+a_0b_0. $

Si on n'est pas convaincu par les points de suspension, on écrira plus précisément :

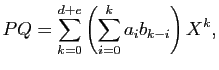
$\displaystyle PQ=\sum_{k=0}^{d+e}\left(\sum_{i=0}^{k}a_ib_{k-i}\right)X^k, $

en ayant préalablement convenu que $ a_i=0$ pour $ i>d$ et $ b_i=0$ pour $ i>e$.

Comme l'anneau a été supposé intègre, le produit $ a_db_e$ n'est pas nul, donc le degré de $ PQ$ est exactement égal à $ d+e$.$ \square$

Définition 5   Pour un polynôme $ P=a_dX^d+a_{d-1}X^{d-1}+\cdots+a_1X+a_0$ non nul dans $ A[X]$, le polynôme dérivé de $ P$ est le polynôme :

$\displaystyle da_dX^{d-1}+(d-1)a_{d-1}X^{d-2}+\cdots+a_1. $

Si $ P=0$, le polynôme dérivé de $ P$ est le polynôme nul.

Notation 4   Le polynôme dérivé de $ P$ est noté $ P'$. Par analogie avec les fonctions, on notera ensuite $ P''$ la dérivée de $ P'$, puis $ P^{(n)}$ la dérivée $ n$-ième.

Proposition 5   Soient $ P$ et $ Q$ deux polynômes de $ A[X]$. Alors :

$\displaystyle (P+Q)'=P'+Q'\qquad{\rm et}\qquad(PQ)'=P'Q+PQ'. $

Démonstration : Simple vérification évidente pour l'addition et ennuyeuse pour la multiplication.$ \square$

Définition 6   Soit

$\displaystyle P=a_dX^d+a_{d-1}X^{d-1}+\cdots+a_1X+a_0$

un polynôme de $ A[X]$ et $ x$ un élément de $ A$. La valeur de $ P$ en $ x$, notée $ P(x)$, est l'élément de $ A$ égal à

$\displaystyle a_dx^d+a_{d-1}x^{d-1}+\cdots+a_1x+a_0 $

Proposition 6   Soient $ P$ et $ Q$ deux polynômes de $ A[X]$ et $ x$ un élément de $ A$. Alors

$\displaystyle (P+Q)(x)=P(x)+Q(x)$   et$\displaystyle \quad (PQ)(x)=P(x)Q(x) $

Démonstration : Simple vérification ; on pourrait aussi énoncer $ 1(x)=1$ qui est évident et complète la collection d'évidences.$ \square$

La notation $ P(x)$ n'a pas que des avantages : elle incite hélas à confondre le polynôme $ P$ avec la fonction qu'il n'est pas. Bien que la notation soit la même, cette définition ne se confond pas avec celle de valeur d'une application en un point.

La définition qui suit cherche à reproduire la notion de composition des fonctions (encore une fois, insistons sur le fait que les polynômes ne sont pas des fonctions). Elle est utilisée une seule fois plus loin, pour écrire la formule de Taylor relative aux polynômes.

Définition 7   Soient $ P$ et $ Q$ deux polynômes de $ A[X]$, avec $ P=a_dX^d+a_{d-1}X^{d-1}+\cdots+a_1X+a_0$. On appelle composé de $ P$ par $ Q$ le polynôme

$\displaystyle a_dQ^d+a_{d-1}Q^{d-1}+\cdots+a_1Q+a_0 $

Notation 5   Ce composé est noté, selon le contexte $ P\circ Q$ ou $ P(Q)$. Typiquement, pour $ Q=X^n$, la notation $ P(X^n)$ s'impose et est d'ailleurs d'interprétation évidente.

Nous terminons cette section par quelques remarques d'algèbre linéaire, valables uniquement dans le cas où l'anneau commutatif des coefficients est un corps $ \mathbb{K}$. Tout d'abord, $ \mathbb{K}[X]$ est un espace vectoriel sur $ \mathbb{K}$. Le plus simple est encore de vérifier à la main la définition des espaces vectoriels, ce que l'on va se garder de faire explicitement ici d'autant que la démonstration sera faite dans le chapitre Espaces vectoriels.

En fait, la définition de l'anneau des polynômes devrait évoquer le concept de base, avec son existence et unicité d'écriture comme une sorte de combinaison linéaire. La seule différence avec les vraies combinaisons linéaires est qu'on va chercher les vecteurs de «base»  dans une famille infinie.

Proposition 7   Soit $ \mathbb{K}$ un corps commutatif. La suite $ (X^i)_{i\in\mathbb{N}}$ est une «base»  de $ \mathbb{K}[X]$ au sens suivant. Pour tout élément $ P$ de $ \mathbb{K}[X]$, il existe une suite unique $ (a_{n})_{n\geqslant 0}$ d'éléments de $ \mathbb{K}$, à support fini, telle que

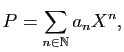
$\displaystyle P=\sum_{n\in\mathbb{N}}a_{n}X^{n}, $

au sens où, si $ N$ est tel que $ a_{n}=0$ pour tout $ n>N$, on a

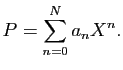
$\displaystyle P=\sum_{n=0}^{N}a_{n}X^{n}. $

La démonstration étant quasiment tautologique, on l'omettra, se bornant à remarquer que seule la deuxième somme, comportant un nombre fini de termes, est bien définie.

Quoi qu'il en soit, $ \mathbb{K}[X]$ est votre premier exemple raisonnablement simple d'espace vectoriel ayant une base infinie. Toutefois, on est toujours plus à l'aise dans les espaces de dimension finie. Il est donc intéressant d'introduire la

Notation 6   Soit $ \mathbb{K}$ un corps commutatif et $ n\geqslant 0$ un entier. On note $ \mathbb{K}_n[X]$ l'ensemble des polynômes sur $ \mathbb{K}$ de degré inférieur ou égal à $ n$.

Proposition 8   Pour tout entier $ n\geqslant 0$, $ \mathbb{K}_n[X]$ est un sous-espace vectoriel de $ \mathbb{K}[X]$. Une base de $ \mathbb{K}_{n}[X]$ est $ (1,X,\ldots,X^n)$. La dimension de $ \mathbb{K}_{n}[X]$ est $ n+1$.

Démonstration : On remarque que $ \mathbb{K}_n[X]$ est l'ensemble engendré par $ (1,X,\ldots,X^n)$ : c'est donc un sous-espace vectoriel. De plus cette famille génératrice est libre (soit par une vérification directe, soit d'après l'unicité de la décomposition de la proposition 7), c'est donc une base de $ \mathbb{K}_n[X]$.$ \square$

Définition 8   La base $ (X^i)_{i\in\mathbb{N}}$ de $ \mathbb{K}[X]$ est appelée sa base canonique.

La base $ (1,X,\ldots,X^n)$ de $ \mathbb{K}_n[X]$ est aussi appelée sa base canonique.

Remarque : Le lecteur pourra avoir l'impression qu'on passe son temps à définir de partout des «bases canoniques» : on en a vu pour $ \mathbb{K}^n$, puis pour les espaces de matrices, et maintenant pour les polynômes. C'est fini pourtant. Insistons bien sur le fait qu'un espace «abstrait»  n'a pas de base canonique : le mot est réservé à certaines bases, remarquables par leur simplicité, d'espaces très particuliers.

Le lemme qui suit servira pour prouver la formule de Taylor et est une redite du chapitre Espaces vectoriels. Un énoncé séparé n'était donc peut-être pas nécessaire mais, même si ce n'est pas indispensable, cela ne peut faire de mal de le connaître ; le plus important étant de comprendre et savoir refaire sa brève démonstration.

Lemme 1   Soit $ \mathbb{K}$ un corps commutatif et $ (P_0,P_1,\ldots,P_n)$ une famille de polynômes de $ \mathbb{K}[X]$ tels que $ 0\leqslant \deg P_0<\deg P_1<\cdots<\deg P_n$. Alors $ (P_0,P_1,\ldots,P_n)$ est une famille libre.

Démonstration : La famille $ (P_0)$ est libre, car il résulte de l'hypothèse $ 0\leqslant \deg P_0$ que $ P_0$ n'est pas nul. Puis le système $ (P_0,P_1)$ est libre puisque $ P_1$, de degré strictement plus grand que $ P_0$, ne peut lui être proportionnel. Puis $ (P_0,P_1,P_2)$ est libre, puisque toute combinaison linéaire de $ (P_0,P_1)$ est de degré inférieur ou égal à $ \deg P_1$ donc $ P_2$ ne peut en être une. Et ainsi de suite (ou plus proprement on fait une récurrence sur $ n$).$ \square$


Section : Cours
Avant : Cours
Après : Arithmétique des polynômes


         © UJF Grenoble, 2011                              Mentions légales