 Les vecteurs
Les vecteurs
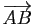 et
et
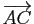 sont égaux.
sont égaux.
-
 Les vecteurs
Les vecteurs
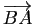 et
et
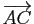 sont égaux.
sont égaux.

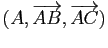 est un repère
affine.
est un repère
affine.
-
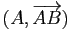 est un repère affine de la droite passant
par
est un repère affine de la droite passant
par 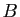 et
et 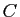 .
.
 Le point
Le point 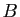 est le milieu du segment
est le milieu du segment ![$ [AC]$](img394.gif) .
.
-
 Le point
Le point 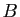 est un barycentre de
est un barycentre de 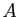 et
et 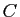 .
.
-
 Le point
Le point 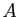 est l'isobarycentre de
est l'isobarycentre de 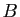 et
et 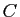 .
.

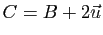 .
.
-
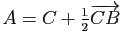 .
.
-
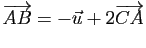 .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales