Nous ne pouvons pas finir, sans exprimer la véritable joie que nous ressentons (que la force de ce sentiment serve d'excuse à notre témérité) de ce que cette découverte a été faite dans notre pays et dans notre temps. Nous nous réjouissons de savoir qu'il s'est élevé un homme capable de comprendre et de compléter le plan du grand architecte, Aristote, de placer la dernière pierre au monument dont les fondations étaient posées depuis deux mille ans, par la main puissante du philosophe de Stagire, et qui après les efforts de tant de générations d'ouvriers...Sir William Stirling Hamilton (1788-1856) n'est pas le Sir William Rowan Hamilton des quaternions et du hamiltonien, et il est beaucoup moins célèbre. Pour quelqu'un censé avoir «complété le plan du grand architecte», n'est-ce pas quelque peu injuste ? Et pour commencer, quelle est cette fameuse «dernière pierre au monument» ? Voici un énoncé, suivi de sa démonstration par contraposée.
Soient ![]() et
et ![]() deux ensembles non vides. Alors :
deux ensembles non vides. Alors :
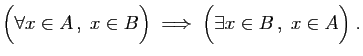

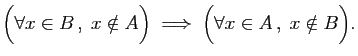
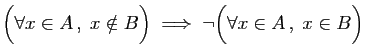
Si A appartient à tout B, B aussi appartient à quelque A ; car si B n'appartenait à aucun A, A n'appartiendrait non plus à aucun B : or A était supposé appartenir à tout B.À part que le second énoncé est nettement plus compréhensible que le premier, qu'est-ce qui les sépare ?
La bagatelle de 23 siècles ! Le second est extrait de l'Organon d'Aristote
(384-322 av. J.C.), le premier n'aurait pas pu être écrit tel
quel avant 1935, date de la première utilisation du symbole ![]() .
Comme ci-dessus, on trouve dans la plupart des énoncés d'Aristote
l'usage de «tout», «aucun» et «
quelque». Selon les différentes combinaisons de «tout» et
«quelque», on distingue 4 types d'affirmations positives
(ni la signification ni la
véracité ne sont en cause) :
.
Comme ci-dessus, on trouve dans la plupart des énoncés d'Aristote
l'usage de «tout», «aucun» et «
quelque». Selon les différentes combinaisons de «tout» et
«quelque», on distingue 4 types d'affirmations positives
(ni la signification ni la
véracité ne sont en cause) :
Ces dithyrambes paraissent un peu exagérés, surtout si l'on réfléchit qu'en réalité Hamilton n'a apporté aucune découverte nouvelle, et que son idée de la quantification du prédicat s'était déjà très nettement présentée à l'esprit du «philosophe de Sagire», - lequel l'avait d'ailleurs rejetée non sans bonnes raisons. À notre connaissance, aucun des critiques modernes de la théorie de Hamilton n'a songé à se reporter sur ce point à la pensée des anciens. Nous avons cependant là un exemple fort remarquable d'une prétendue innovation non pas seulement, comme tant d'autres, déjà contenue, plus ou moins implicitement, dans l'arsenal des vieux auteurs, et élucidable par leurs principes, mais bien formulée explicitement et explicitement critiquée par eux. Bien plus, si pertinente que soit la réfutation présentée par de Morgan et par Stuart Mill de la théorie de la quantification du prédicat, nulle critique moderne de cette théorie n'est aussi décisive et aussi pénétrante que la page qui lui est consacrée par Saint Thomas d'Acquin dans son commentaire sur le Perri Hermeneias.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales