Essayez de bien rédiger vos réponses, sans vous
reporter ni au cours, ni au corrigé.
Si vous souhaitez vous évaluer, donnez-vous deux heures ; puis comparez
vos réponses avec le corrigé et comptez un point pour
chaque question à laquelle vous aurez correctement répondu.
Questions de cours : Soient  et
et 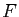 deux ensembles. Soit
deux ensembles. Soit  une application de
une application de  dans
dans
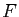 . Soit
. Soit  un sous-ensemble de
un sous-ensemble de  et
et 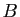 un sous-ensemble de
un sous-ensemble de 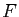 .
.
- Définir l'image
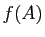 de
de  et l'image réciproque
et l'image réciproque
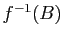 de
de 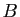 .
.
- Démontrer que
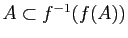 et que
et que
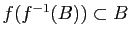 .
.
- Quand dit-on que
 est injective ? surjective ?
est injective ? surjective ?
- Démontrer que si
 est injective, alors
est injective, alors
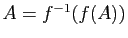 . Démontrer que si
. Démontrer que si  est surjective, alors
est surjective, alors
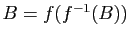 .
.
- Soit
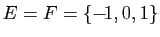 et soit
et soit  l'application de
l'application de  dans
dans 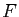 qui
à
qui
à 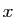 associe
associe 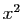 . L'application
. L'application  est-elle injective ?
surjective ? Soit
est-elle injective ?
surjective ? Soit 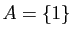 et
et
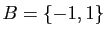 . Ecrire en extension les
ensembles
. Ecrire en extension les
ensembles
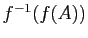 et
et
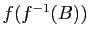 .
.
Exercice 1 :Soient  ,
, 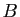 et
et 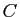 trois assertions.
trois assertions.
- Ecrire la table de vérité de l'assertion :
- Ecrire la table de vérité de l'assertion :
- Utiliser les tables de vérité des deux questions
précédentes pour démontrer que l'équivalence suivante est
toujours vraie.
- En utilisant les assertions
 : «je suis une fille»,
: «je suis une fille»,
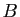 : «je fais du sport » et
: «je fais du sport » et 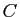 : «je garde la forme»,
exprimer en langage courant l'équivalence de la question
précédente.
: «je garde la forme»,
exprimer en langage courant l'équivalence de la question
précédente.
- Soit
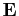 un ensemble,
un ensemble,
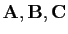 trois sous-ensembles de
trois sous-ensembles de  .
Représenter dans trois diagrammes de Venn différents
les ensembles
.
Représenter dans trois diagrammes de Venn différents
les ensembles
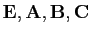 , dans les trois cas suivants.
, dans les trois cas suivants.
-
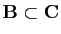 .
.
-
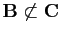 ,
,
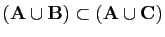 ,
,
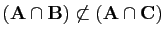 .
.
-
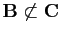 ,
,
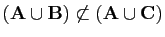 ,
,
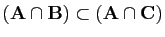 .
.
- Démontrer que l'équivalence suivante est toujours vraie.
Exercice 2 :
- Soient
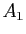 et
et 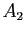 deux assertions. Ecrire à l'aide des symboles
deux assertions. Ecrire à l'aide des symboles
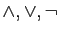 l'assertion : «de deux choses l'une, soit
l'assertion : «de deux choses l'une, soit 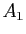 est vraie, soit
est vraie, soit 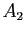 est vraie, mais pas les deux». On notera
désormais
est vraie, mais pas les deux». On notera
désormais
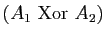 cette assertion.
cette assertion.
- Démontrer à l'aide des tables de vérité
que l'implication suivante est
toujours vraie.
- On considère les propositions suivantes :
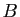 : «je bois»,
: «je bois»,
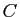 :«je conduis»,
:«je conduis», 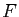 : «je vais voir un film»,
: «je vais voir un film», 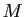 : «je
marche»,
: «je
marche», 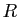 : «je
vais au restaurant».
Ecrire sous forme symbolique les assertions suivantes.
: «je
vais au restaurant».
Ecrire sous forme symbolique les assertions suivantes.
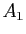 :
:- «de deux choses l'une, soit je conduis, soit je marche».
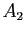 :
:- «de deux choses l'une, soit je vais voir un film, soit je vais au
restaurant, et dans ce cas je bois».
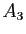 :
:- «si je conduis, alors je ne bois pas».
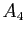 :
:- «je ne marche pas».
- On suppose que les assertions
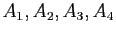 sont
vraies. Démontrer que l'assertion
sont
vraies. Démontrer que l'assertion 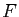 est vraie. Vous écrirez
votre raisonnement sous forme symbolique, et en langage courant.
est vraie. Vous écrirez
votre raisonnement sous forme symbolique, et en langage courant.
Exercice 3 :Soit 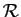 la relation définie sur l'ensemble des réels
la relation définie sur l'ensemble des réels
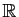 par :
par :
Soit 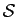 la relation définie sur l'ensemble des réels
la relation définie sur l'ensemble des réels
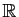 par :
par :
- Montrer que
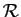 est une relation d'équivalence.
est une relation d'équivalence.
- Démontrer que pour tout
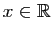 ,
,
- Démontrer que la relation
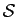 est réflexive, transitive, mais
qu'elle n'est ni symétrique ni anti-symétrique.
est réflexive, transitive, mais
qu'elle n'est ni symétrique ni anti-symétrique.
- Soit
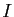 l'ensemble des réels supérieurs ou égaux à
l'ensemble des réels supérieurs ou égaux à
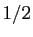 . Soit
. Soit 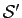 la relation définie sur
la relation définie sur 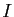 par :
par :
Montrer que 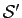 est une relation d'ordre sur
est une relation d'ordre sur 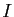 .
.
- Démontrer que :
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() et
et ![]() deux ensembles. Soit
deux ensembles. Soit ![]() une application de
une application de ![]() dans
dans
![]() . Soit
. Soit ![]() un sous-ensemble de
un sous-ensemble de ![]() et
et ![]() un sous-ensemble de
un sous-ensemble de ![]() .
.
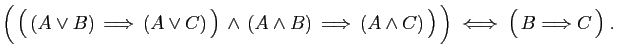
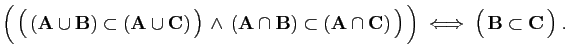
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales