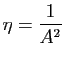 . Alors :
. Alors :
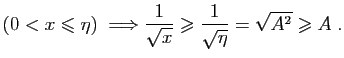
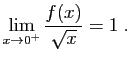
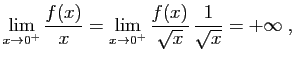
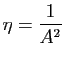 . Alors :
. Alors :
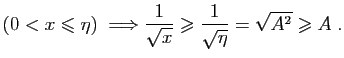
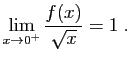
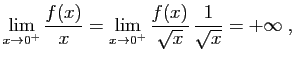
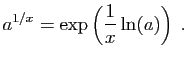
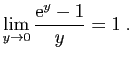
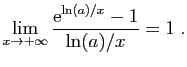
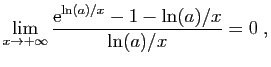
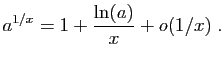
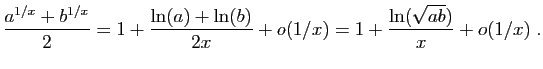
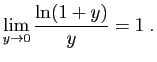
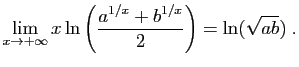
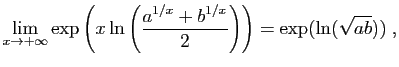
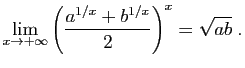
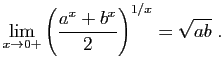
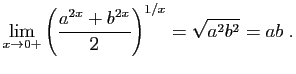
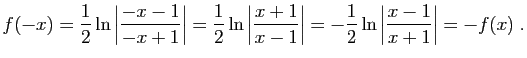
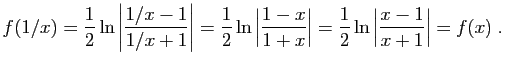
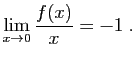
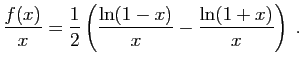
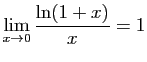 donc
donc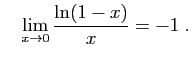
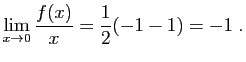
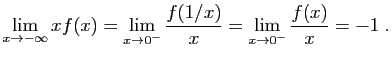
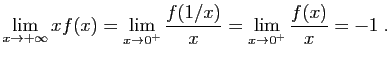
La fonction
![]() est continue en
est continue en ![]() . Donc :
. Donc :
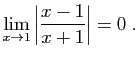
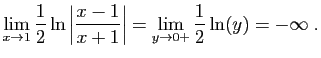
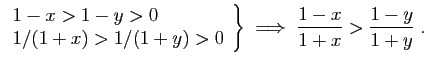
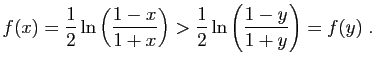
| si |
| si |
Si
![]() , alors :
, alors :
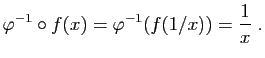
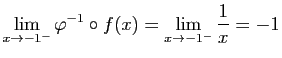 et
etDe même :
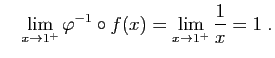
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales