- La limite à droite de
 en 0 est
en 0 est 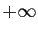 si et seulement si
si et seulement si
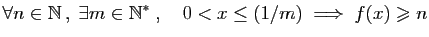
- La limite à droite de
 en 0 est
en 0 est 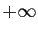 si et seulement si,
pour toute suite
si et seulement si,
pour toute suite 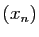 de réels strictement positifs, convergeant
vers 0, la suite
de réels strictement positifs, convergeant
vers 0, la suite 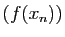 tend vers
tend vers 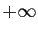 .
.
- La limite à droite de
 en 0 est
en 0 est 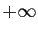 si et seulement
si pour tout
si et seulement
si pour tout
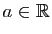 ,
,
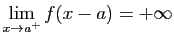
- La limite à droite de
 en 0 est
en 0 est 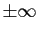 si et seulement
si :
si et seulement
si :
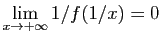
- Si la limite à droite de
 et de
et de 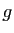 en 0 est
en 0 est 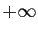 , alors
il en est de même pour
, alors
il en est de même pour 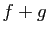 et
et 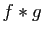 .
.
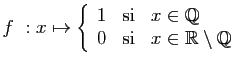
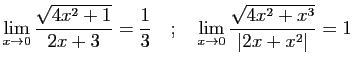
![$\displaystyle \displaystyle{\lim_{x\rightarrow 0}
\frac{x+\sqrt{\vert x\vert}}...
...rt x\vert}+\sqrt{\vert x\vert}}{\sqrt[3]{\vert x\vert}-\sqrt{\vert x\vert}}=1}
$](img444.gif)
![$\displaystyle \displaystyle{\lim_{x\rightarrow 0}
\frac{\sqrt{1+x}-\sqrt{1-x}}...
...lim_{x\rightarrow +\infty} \frac{\sqrt[3]{1+x}-
\sqrt[3]{1-x}}{x}=\frac{2}{3}}
$](img445.gif)
![$\displaystyle \displaystyle{\lim_{x\rightarrow +\infty}
\frac{\sqrt{4x^2+1}}{2...
...{x\rightarrow +\infty}
\frac{\sqrt[3]{x^6+3x^4+1}}{\sqrt{4x^4-3}}=\frac{1}{2}}
$](img446.gif)
![$\displaystyle \displaystyle{\lim_{x\rightarrow +\infty}
\frac{x+\sqrt{x}}{x-\s...
..._{x\rightarrow +\infty}
\frac{\sqrt[3]{x}+\sqrt{x}}{\sqrt[3]{x}-\sqrt{x}}=-1}
$](img447.gif)
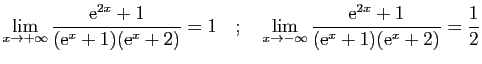
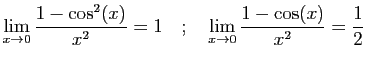
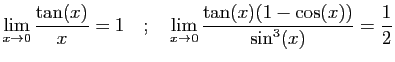
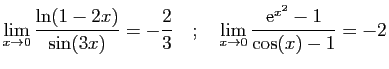
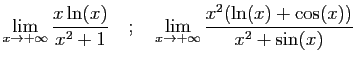
![$\displaystyle \lim_{x\rightarrow +\infty} \frac{\mathrm{e}^{\sqrt{x}}}{x^2}
\qu...
...uad
\lim_{x\rightarrow +\infty}
\frac{\mathrm{e}^{-\sqrt[3]{x}}}{x^3\ln^3(x)}
$](img456.gif)
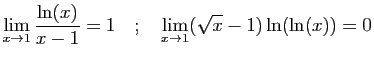
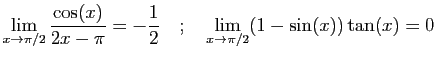
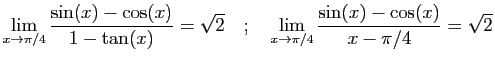
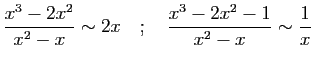
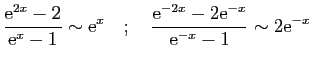
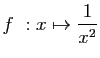
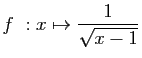
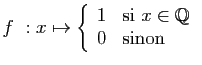
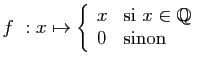
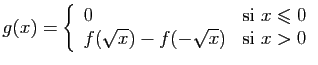
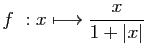
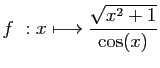
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales